参考:DR_CAN
1.介绍
解决一个控制系统的问题:
- 对研究对象进行分析
- 控制器设计
- 测试
分析被控对象的物理特性及动态表现,在这个基础上建立数学模型,数学模型可以是动力学模型、热力学模型、流体力学模型和经济学模型等,然后在数学模型的基础上进行控制器的设计,为满足不同的要求就要应用不同的控制方法(传统控制控制、PID控制、非线性控制、自适应控制和优化控制等),紧接着选择测试平台,可以是仿真平台、实验室模型样机和真实设备等。最后不断将实验结果与模型比较,对数学模型不断的验证和更新。
涉及的内容: 动态系统建模:
- 电力,KCL,KVL
- 流体
- 热力学
- 机械系统
拉普拉斯+微分方程 时域分析 频域分析
2.电路系统建模
基础元件:
流速:
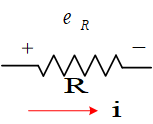
电阻电压:
电量:
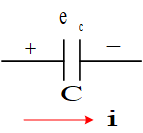
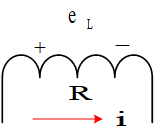
电感:
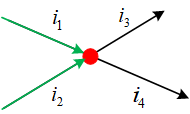
基尔霍夫定律 KCL:所有进入某节点的电流的总和等于所有离开这个节点的电流的总和
KVL:沿着闭合回路所有元件两端的电压的代数和为零
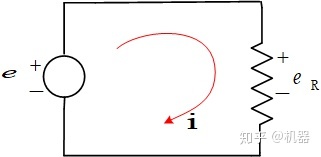
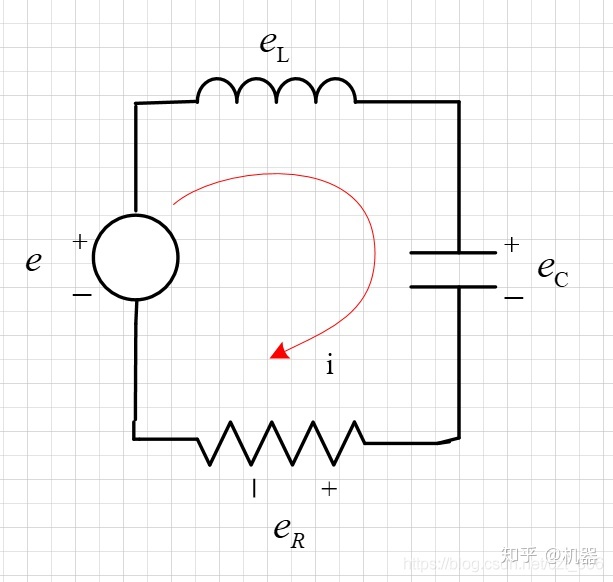
KVL
两边求导
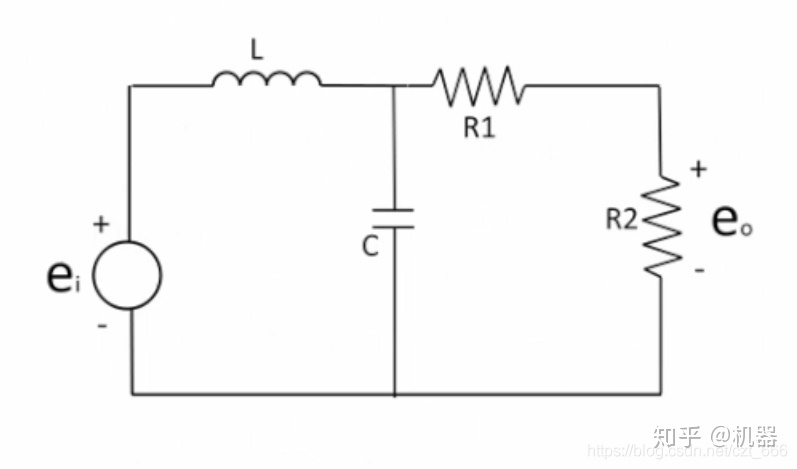
loop 1:
loop 2:
合并:
这是一个大圈,因此在用KVL时,不一定都用小圈,也可用大圈。
loop 1:
loop 2:
由(1)(2)式得
由(2)得
由(3)(4)式得
求
由(5)(6)式得
小结: KVL列方程,然后消掉自己定义的电流
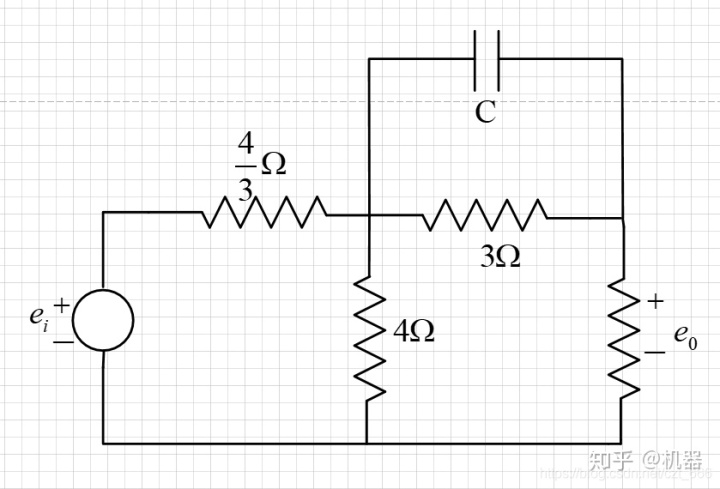
loop 1:
loop 2:
loop 3:
我们的目的是找到
由(1)(2)式得
由(3)(4)式得
(5)式还有
由(5)(6)式得
只有电流
3.流体系统建模
流体系统的几个基本元素: 此处默认为不可压缩的均质流体
压强有三个概念,比如说对于容器的液体来说,它的高度是
除了液体的压强以外还有大气压强,绝对压强(Absolute Pressure)
测量出来的压力称为表压(Gauge Pressure)
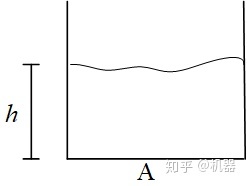
流阻Fluid Resistance 产生流阻的原因是流体在流动的过程中,通过一些管道连接等,这些都会阻碍流体的流动,因此会产生压差,压差和流量相关
流阻和电阻的概念非常相似
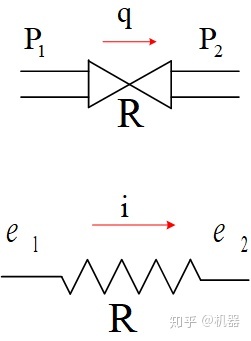
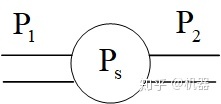
理想压源
基本法则-质量守恒定律Conseration of Mass 有了基本元素,还需要基本法则把它们联系在一起,就像电路当中有基尔霍夫定律,在力学当中有牛顿定律一样,这里面我们用到的是质量守恒定律,容器内流体质量的变化
式子两边除以
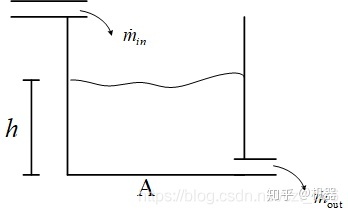
容器底部受到的压力
其动态方程为
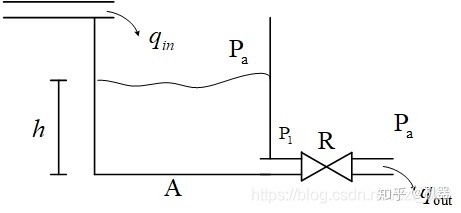
进口处为
由质量守恒定律
流阻压差
4.拉普拉斯变换
拉普拉斯变换是控制理论的基础,它广泛的应用于工程分析当中,它可以把时域(
先从一个简单的电路系统开始,它的动态方程
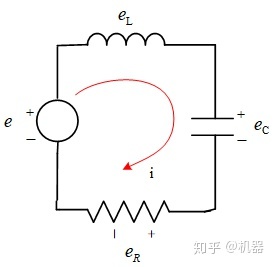
定义系统的输入为
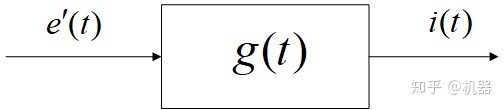
对时域函数
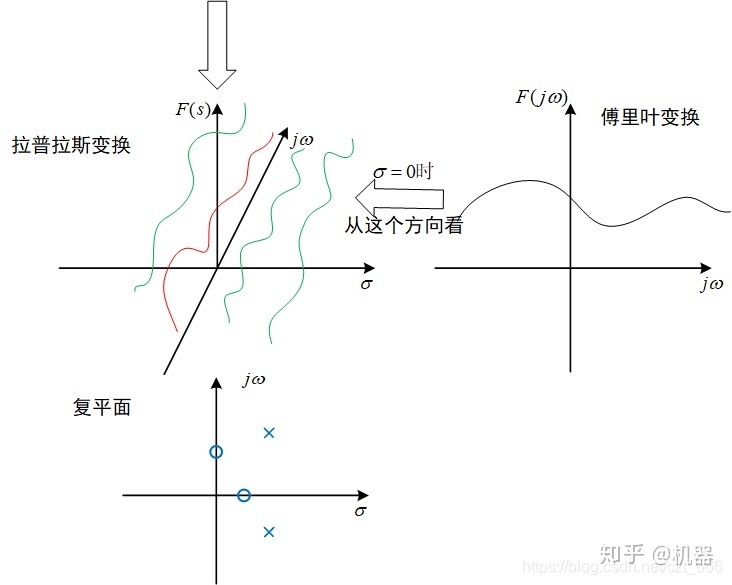
从上向下看就是复平面,做工程的往往会关注系统的极点和零点在复平面上的位置.
指数函数
拉普拉斯变换的重要性质:符合线性变换,线性变换符合叠加原理
正弦
两式相减:
因为拉普拉斯变换是一个线性变换:
导数的拉普拉斯变换:
复合函数求积分,用到分部积分:
同理可得
卷积的拉普拉斯变换 能够将卷积运算变成乘积运算,大大简化运算和分析的复杂程度。
回到最初的电路的动态方程:
两端作拉普拉斯变换:
可以看到,经过拉普拉斯变换把微分方程变换为代数方程,它只有加减乘除,非常的简单。下图方框称之为传递函数。

5.拉普拉斯变换的收敛域(ROC)与逆变换(ILT)
指数函数的拉普拉斯变换:
如果
加上限制条件,收敛域ROC(Region of lonvergence),把
根据欧拉公式:
前面我们已经知道,拉普拉斯能简化运算和分析,为什么还需要微分方程?因为微分方程能够描述动态世界的数学手段。
在经典控制理论和现代控制理论当中,研究对象一般是常系数微分方程,对应的系统就是线性时不变系统,如果是非线性系统的话,一般会在平衡点附近作线性化处理,或者直接采用非线性分析手段。
用拉普拉斯变换求解微分方程的三个步骤:
- 时域转化到复频域
,这里用到拉普拉斯变换
- 求解代数方程
- 把结果从复频域转回时域,用到拉普拉斯逆变换
拉普拉斯逆变换
例子
两端拉普拉斯逆变换:
其中,根据欧拉公式有
(2)-(1)
6.拉&传&微的关系
重点讲解传递函数
这部分内容非常重要,对经典控制理论、根轨迹、伯德图、信号处理等学习都有很大的帮助,因为都是从这里伸展出去的。
流体系统

令A=1
两端作拉普拉斯变换:

假设系统的输入为常数,对常数作拉普拉斯变换
当时间

7.一阶系统的单位阶跃响应
流体系统

动态方程:
输出是一阶,输入是单位阶跃,称为一阶系统的单位阶跃响应 Unit Step Response.
一般形式:

两边作拉普拉斯逆变换:
a越大收敛越快。
时间常数 time constant
即

有时候还会引入另一个概念-稳定时间(Steady State)(整定时间)Setting time
对于一阶线性系统来说,时间常数是特有的,因此可以用时间常数作系统识别。
根据上一节有:

4秒钟达到稳定时间:
系统的传递函数:
一阶系统与信号处理
一阶系统是一个低通滤波器,低通滤波器只反映了低频变化,高频变化则被过滤了。对于流体系统来说,容器内的液体就起到了抵抗高速变化的作用,是因为它有积累,所以说有积累的都是低通滤波器,它对高速变化不敏感。最典型的积累就是积分,如:
高频变化被缩放100倍,相当于被过滤掉了。所以说大家平时多做积累,有了容量以后面对高速变化的世界才可以做到处乱不惊。

另一个角度
一阶线性时不变系统1st order LTI:


其他情况,

Phase-Portrait
8.频率响应与滤波器
信号通过线性时不变系统后频率不变
振幅响应 Magnitude Response:
辐角响应 Phase Response:

一般形式:

两边作拉普拉斯变换:
其中,
拉普拉斯逆变换:
对于稳定系统,
ss:Steady State 稳态,由上式可以看出频率响应就是稳态响应。求
复数表达:
欧拉公式:
非常非常的重要:
积分

例子:
9.一阶系统的频率响应
一阶系统:

当
当
当

所以一阶系统的频率响应是一个低通滤波
总结: 无论是室内空调系统、流体系统还是含电容器的电路系统,容器就是一个缓冲器,其本质是抑制高速变化。缓冲也会带来延迟。

Matlab 仿真
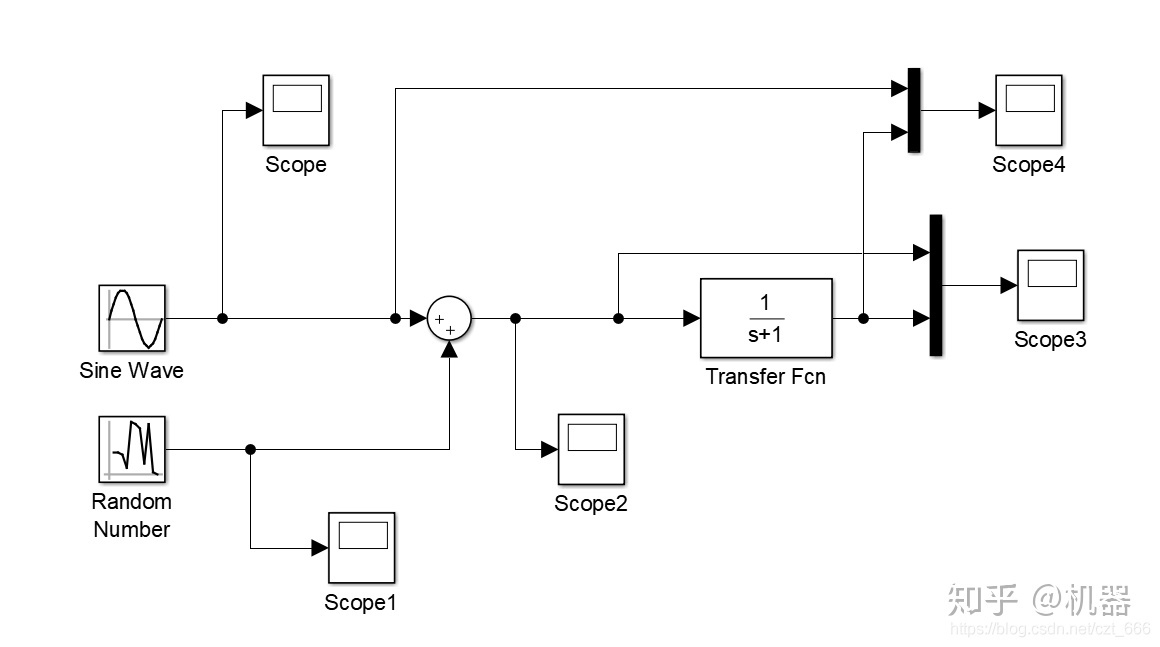
积分前后的对比

滤波信号后与原函数的对比 滤波信号延迟45°,振幅变为0.707左右

把纵轴改为

10.二阶系统对初始条件的动态响应
二阶系统无处不在,运动现象普遍是二阶系统,如牛顿第二定律
质量弹簧阻尼系统

阻尼和速度成正比,牛顿第二定律:
研究零初始条件,无外力的情况下:
将条件代入:
simulink
位置为5,速度为0

特征方程 Characteristic Equation:
过阻尼Over damped

- 临界阻尼Critial damped
比过阻尼收敛速度快一些

- 欠阻尼Under damped
其中
从

这是正弦函数,没有衰减

11.二阶系统的单位阶跃响应
弹簧质量阻尼系统

输入:
上一节用的是微分方程的通解和特解,这小节用拉普拉斯变换:
传递函数:

- 单位阶跃
极点
欠阻尼
因此是震荡衰减的。
Matlab 仿真



12.二阶系统的性能分析与比较
如何衡量系统的性能?
欠阻尼动态响应:

5%
分析手段和方法

- 计分规则:1分,2分,3分
雷达图

13.二阶系统频率响应分析
不同阻尼比的频率响应
振幅响应:
辐角响应:
用这个结论分析二阶系统
传递函数:
其中
振幅响应:
分析
,输入频率等于固有频率
因此在
当
这个频率称为系统的谐振振频率,
当输入频率等于谐振频率时:
时:
时:
时:
对于阻尼比比较小的系统来说,如果外力的频率在谐振频率(极值)附近,那么系统就会表现出强烈的振幅响应,不同的系统有不同的谐振频率,对外界刺激响应也就不同。
不同阻尼比的频率响应
14.伯德图
伯德图是表示频率响应的图示方法,频率响纵坐标改为
对于传递函数:
直接在命令窗口输入:
>> bode([1 2],[1 4])
dB decibel 分贝 dec 指十分之一,bel人名,分贝表示的是电话、电报的信号损失
加对数是为了把较大的数值降低,便于记录,如
振幅和功率为平方关系
积分
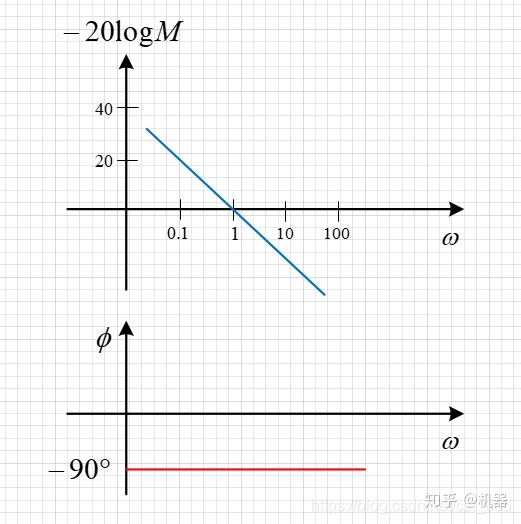
低频
截至频率
高频

例:
拆分
>> bode([0 1],[0 2])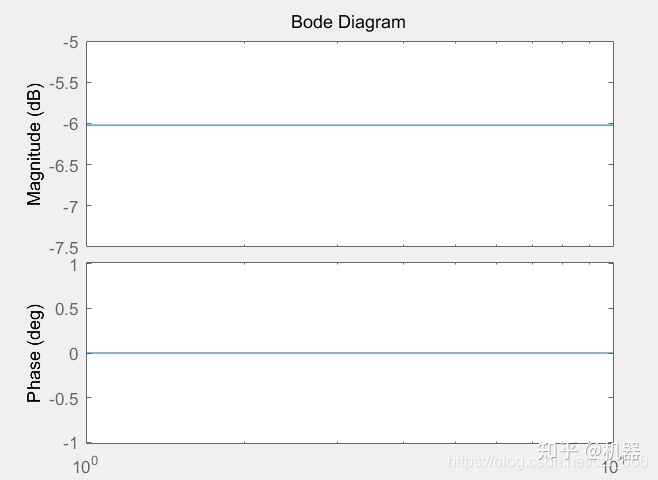
>> bode([1/4 1],[0 1])
>> bode([0 1],[1/8 1])
>> bode([1 4],[1 8])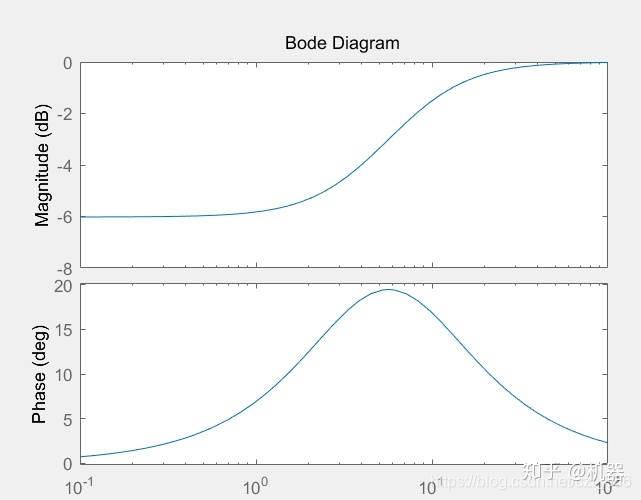
)
)



——通过matlab工具箱设计FIR数字滤波器...)













