1、引言
“物以类聚、人以群分”。但我们面对一群人或者一堆物的时候,我们都希望将他们分分类,分类之后,我们才能更加有针对性地采取措施,从而提高工作效率。
如,我们将消费者分成若干类,有的是土豪、有的是工薪阶层,然后我们就采取不同的营销策略。再比如,我们将交通出行者分成若干类,有的是公共交通出行、有的是打车出行、有的是私车出行等,然后采取不同服务措施。
分类的方法很多,这里介绍一种称之为聚类分析的方法。更准确的说,聚类分析也有很多种类,这里仅仅介绍其中最为基础的一种,称之为层次聚类分析。
2、层次聚类分析原理
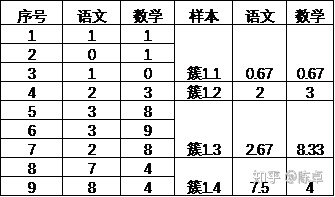
现在假设,我们有9名同学,参加满分为10分的语文和数学考试。他们的成绩,见表1。
表1 9名同学的语文和数学成绩

为了便于观察,我们用散点图描述学生的成绩,如图1所示。

图1 9名同学成绩在两维空间上的分布
从图1我们可以看出,9名学生大约可以分为三类。
第一类由编号为1、2、3、4的学生组成,它们的特点是语文和数学成绩都不太好。
第二类由编号为5、6、7的同学组成,他们的特点是语文成绩一般,但数学成绩较好。
第三类由编号为8、9的同学组成,他们的特点是语文较好,但数学成绩不太好。
三类学生特点不同,也决定着下一步学习特点不同。因此,有效地分类,可以提高教学的针对性。
然而这个分类是根据肉眼观察得到的,并不严谨。下面,我们介绍如何通过数学的方法分析得到。
首先,我们需要明确,分类的依据是学生成绩之间的距离。距离越小,则他们越可能分到同一个类别中;距离越大,则他们越不可能分到同一个类别中。
描述他们之间距离的公式很多,不同公式应用在不同场合,这也表明了聚类分析内容的丰富性。
其中一个经典的公式是用来计算马氏距离的公式。简单说就是,两点之间的距离等于他们的横坐标之差的平方加纵坐标之差的平方的开方,用数学公式表示为
由此我们可以得到这9名同学学习成绩之间的距离,见表2。
表2 9名学生的学习成绩之间的距离

从表2中可以看出,在所有32个距离中,最小的距离为1,为学生1与学生2、3的距离、学生5与学生6、7的距离,以及学生8与学生9之间的距离。
据此,我们将学生1、2、3合并作为一类,5、6、7合并作为一类、8、9合并作为一类,学生4单独作为一类。这样,9名同学分为4类,分别命名为{簇1.1,簇1.2,簇1.3,簇1.4 }。
但是,假如我们只有两个老师,必须讲9名同学分成两类。那么就需要在上述4类基础上继续划分。
首先,我们需要找到一个代表值来代表各类。这种代表方法很多,一般教材提供了8种。(这也说明聚类分析内容的丰富性。)
这里选择其中一种,叫做中心点法,简单说就算平均值。如,类1包含{1,2,3},其坐标值为{(1,1),(0,1),(1,0)},其平均值为(0.67,0.67)。我们用坐标为(0.67,0.67),代表一类。
这样,{簇1.1,簇1.2,簇1.3,簇1.4 }的坐标值,见表3。
表3 第一次聚类后的各簇中心点分布
在空间上的分布,如图2所示。
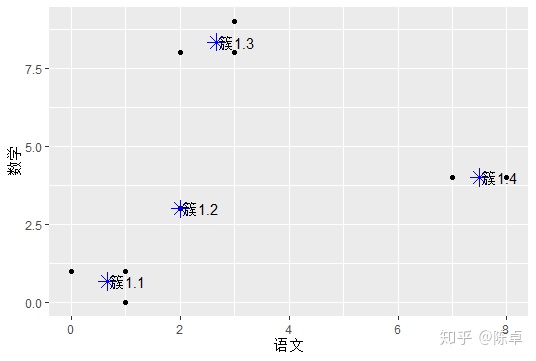
图2 第一次聚类后各簇中心点分布情况
在图2中,黑色点表示原来9名学生的成绩。而蓝色米状点则表示各簇的中心点,以代表各簇。
为进一步聚类,计算它们之间的距离,结果见表4。
表4 第一次聚类后各簇之间的距离
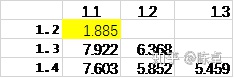
根据表4的结果,簇1.1 和簇1.2距离较近,合并,形成簇2.1。簇1.2、簇1.3,未与其他簇合并,保留下来,分别命名为簇2.2、簇2.3。
这样{簇2.1、簇2.2、簇2.3}的坐标,见表5。
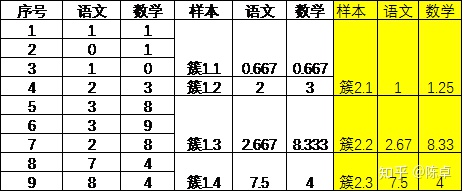
表5 第二次聚类后各簇的坐标
需要注意的是,簇2.1 的坐标不是簇1.1和簇1.2 的坐标的平均值,而是簇1.1和簇1.2 中所有学生的成绩的平均值,因此为(1,1.25)。
其在空间上的分布,如图3所示。
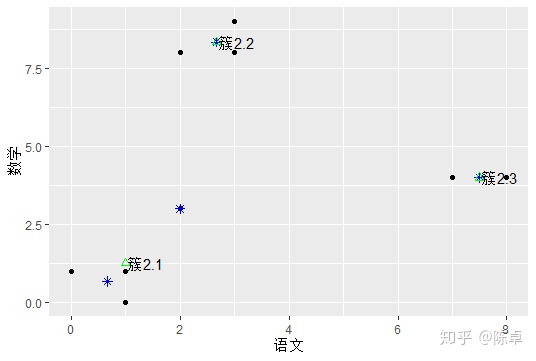
图3 第二次聚类后各簇的位置
图3中,绿色三角表示第二次聚类后各簇的中心位置。
继续计算簇2.1、簇2.2、簇2.3 的距离,见表6。
表6 {簇2.1、簇2.2、簇2.3}之间的距离

从表6可以看出,簇2.2和2.3 距离更近,它们可以合并。这样就形成了两类{簇3.1、簇3.2}。
绘制出{簇3.1和簇3.2}的位置,如图4所示。途中,红色田字表示簇3.1和簇3.2的位置。
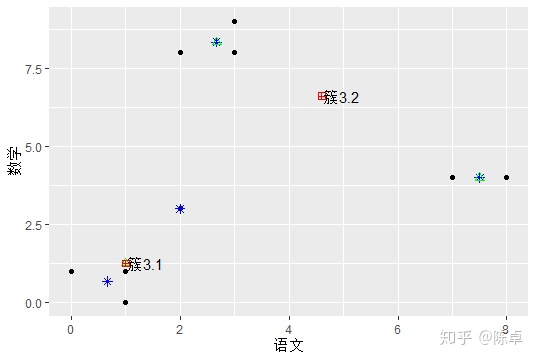
图4 第三次聚类后各簇位置
簇3.1和簇3.2都是9名同学经过三次合并(聚类)得到的,其中簇3.1 是由{1、2、3、4}等4名同学合并,包含着簇2.1、簇1.1和簇1.2。簇3.2 是由{5、6、7、8、9}等5名同学合并的,包含着簇2.2、簇2.3、簇1.3和1.4。
3、聚类分析在R语言中实现
前面用冗长的文字介绍了聚类分析的过程,从而揭示聚类分析的原理。在R语言中,我们用4句代码,实现上述过程。
# 输入原始数据
dt1<-as.data.frame(cbind(c(1,0,1,2,3,3,2,7,8),c(1,1,0,3,8,9,8,4,4)))
# 给各列命名
colnames(dt1)<-c("语文","数学")
#因为下面的hclust只能处理矩阵,因此需要计算距离矩阵。
result <- dist(dt1)
#调用hclust函数,生成聚类结果
result_hc <- hclust(d = result, method = "average")
#将聚类结果展示出来
plot(result_hc,main="聚类结果",ylab="距离",xlab="学生")

图5 聚类分析结果
图5以一个树状图的方式描述各个学生之间距离远近。从下而上可以观察,1和2距离较近,合并为一类;然后1、2与3较近,合并为一类;再然后与4相近,合并为一类;另一个方向上,5、6接近合并为一类,然后与7合并为一类,8与9合并为一类,再与{5、6、7}合并为一类。最后,将这9类合并在一起。
研究者可以根据自己需要对9名学生进行分类。具体来说,研究者可以用一个水平线对树状图进行切割。如,水平线处于距离为3.5的地方,它与树状图有3处相交,则将9名学生分为3类,分别是{1,2,3,4}、{5、6、7}、{8,9};水平线处于距离为2.5的地方,则它与树状图4处相交,从而将9名学生分为4类,分别是{1、2、3}、{4}、{5、6、7}、{8、9}。



















