一、背包问题

1.1 01背包问题

特点:每件物品最多只用于一次

 属性包括:最大值(Max)、最小值(Min)、数量

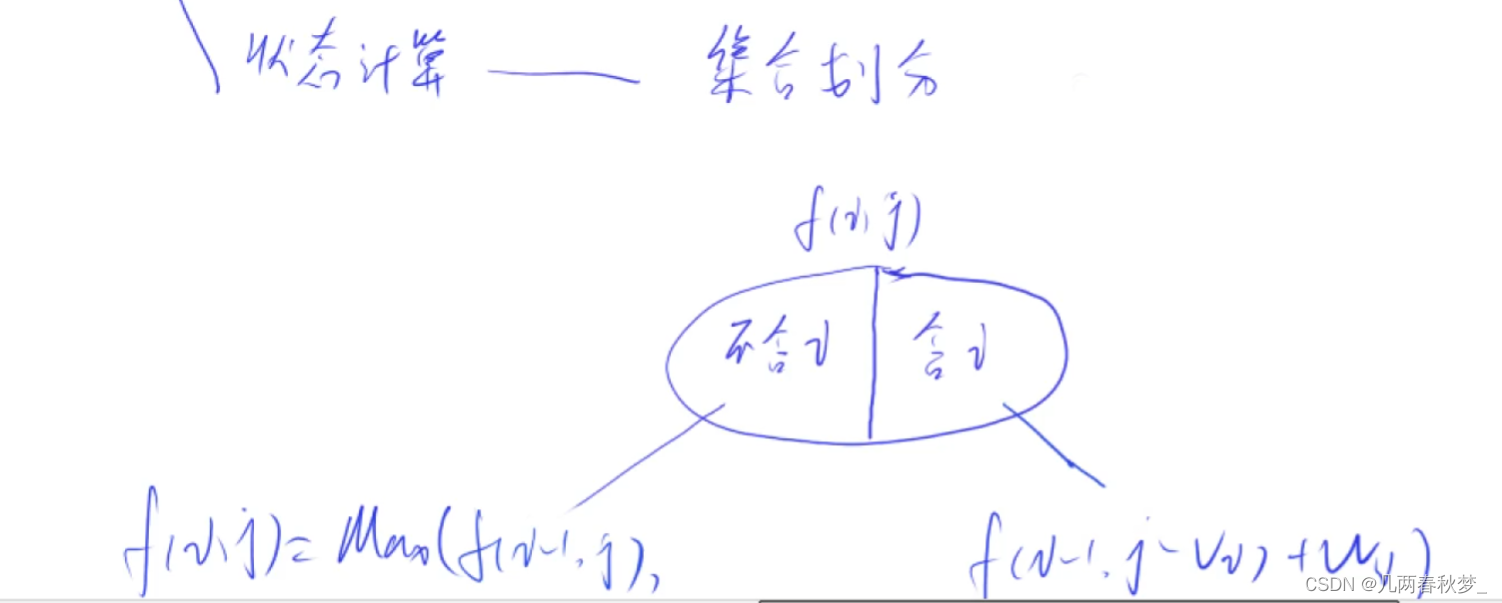
#include<iostream>
#include<algorithm>using namespace std;const int N = 1010;int n,m;
int v[N],w[N];
int f[N][N];int main()
{cin>>n>>m;for(int i = 1;i <= n; i++) cin>>v[i]>>w[i];for(int i = 1;i <= n;i ++){for(int j = 0;j <= m;j ++){f[i][j] = f[i - 1][j];if(j >= v[i]) f[i][j] = max(f[i][j],f[i - 1][j - v[i]] + w[i]);}}cout<<f[n][m]<<endl;return 0;
}

1.2 完全背包问题

特点:每件物品有无限个

#include<iostream>
#include<algorithm>using namespace std;const int N = 1010;int n,m;
int v[N],w[N];
int f[N][N];int mian()
{cin>>n>>m;for(int i = 1;i <= n;i ++) cin>>v[i]>>w[i];for(int i = 1;i <= n;i ++)for(int j = 0; j <= m;j ++)for(int k = 0;k * v[i] <= j; k ++)f[i][j] = max(f[i][j],f[i - 1][j - v[i] * k] + w[i] * k);cout<<f[n][m]<<endl;return 0;
}

1.3 多重背包问题

特点:每个物品的个数不同

#include<iostream>
#include<algorithm>using namespace std;const int N = 25000,M = 2010;int n,m;
int v[N],w[N];
int f[N];int main()
{cin>>n>>m;int cnt = 0;for(int i = 1;i <= n;i ++){int a,b,s;cin>>a>>b>>s;int k = 1;while(k <= s){cnt ++;v[cnt] = a * k;w[cnt] = b * k;s -= k;k *= 2;}if(s > 0){cnt ++;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt;for(int i = 1;i <= n;i ++)for(int j = m;j >= v[i];j --)f[j] = max(f[j],f[j - v[i]] + w[i]);cout<<f[m]<<endl;return 0;
}

1.4分组背包问题

特点:物品有n组，每一组物品中有若干个

#include<iostream>
#include<algorithm>using namespace std;const int N = 110;int n,m;
int v[N][N],w[N][N],s[N];
int f[N];int main()
{cin>>n>>m;for(int i = 1;i <= n;i ++){cin>>s[i];for(int j = 0;j < s[i];j ++){cin>>v[i][j]>>w[i][j];}}for(int i = 1;i <= n;i ++)for(int j = m;j >= 0;j --)for(int k = 0;k < s[i];k ++)if(v[i][k] <= j)f[j] = max(f[j],f[j - v[i][k]] + w[i][k]);cout<<f[m]<<endl;return 0;
}