机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索,Glodstein Condition]
引言
上一节介绍了 Armijo \text{Armijo} Armijo准则 ( Armijo Condition ) (\text{Armijo Condition}) (Armijo Condition),本节将继续介绍 Glodstein \text{Glodstein} Glodstein准则 ( Glodstein Condition ) (\text{Glodstein Condition}) (Glodstein Condition)。
回顾: Armijo Condition \text{Armijo Condition} Armijo Condition
首先,希望数值解对应的目标函数结果 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞收敛至最优解 f ∗ f^* f∗:
{ f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
而数值解对应的目标函数结果满足严格的单调性是一项不可忽视的重要因素:
{ f ( x k + 1 ) = f ( x k + α ⋅ P k ) = ϕ ( α ) ϕ ( α ) = f ( x k + 1 ) < f ( x k ) = ϕ ( 0 ) \begin{cases} \begin{aligned} & f(x_{k+1}) = f(x_k + \alpha \cdot \mathcal P_k) = \phi(\alpha) \\ & \phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \end{aligned} \end{cases} {f(xk+1)=f(xk+α⋅Pk)=ϕ(α)ϕ(α)=f(xk+1)<f(xk)=ϕ(0)
但仅仅满足 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从严格的单调性不足以证明 { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗。也就是说:后者是前者的必要不充分条件。
关于不充分性质的反例,见传送门
Armijo \text{Armijo} Armijo准则产生的动机在于:条件 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)的约束能力太松散。而具体表现在: ϕ ( α ) \phi(\alpha) ϕ(α)函数中,满足条件 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)的 α \alpha α值过多,反而对优秀步长结果的选择产生阻碍:

观察上图,其中:
- 蓝色曲线表示 ϕ ( α ) \phi(\alpha) ϕ(α)的函数曲线;
- 红色虚线表示步长 α \alpha α的划分边界 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)。因而 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)描述的是红色虚线下方的部分,具体对应步长 α \alpha α的选择范围见 α \alpha α轴上的红色实线。
Armijo Condition \text{Armijo Condition} Armijo Condition关于 f ( x k + 1 ) < f ( x k ) f(x_{k+1})< f(x_k) f(xk+1)<f(xk)条件过于松散的处理方法是:相比于上图中的红色虚线,尝试找到一条更优的直线对 ϕ ( α ) \phi(\alpha) ϕ(α)进行划分,最终使步长 α \alpha α的选择范围明显降低。
它选择了 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)与 ϕ ( α ) \phi(\alpha) ϕ(α)在 α = 0 \alpha=0 α=0处的切线函数: l ( α ) = f ( x k ) + [ ∇ f ( x k ) ] T P k ⋅ α l(\alpha) = f(x_k) + [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha l(α)=f(xk)+[∇f(xk)]TPk⋅α进行组合,其划分边界函数表示为:
L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α C 1 ∈ ( 0 , 1 ) \mathcal L(\alpha) = f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \quad \mathcal C_1 \in (0,1) L(α)=f(xk)+C1⋅[∇f(xk)]TPk⋅αC1∈(0,1)
由于 C 1 > 0 , α > 0 \mathcal C_1 >0,\alpha>0 C1>0,α>0(步长的物理意义);并且 [ ∇ f ( x k ) ] T P k < 0 \left[\nabla f(x_k)\right]^T \mathcal P_k < 0 [∇f(xk)]TPk<0,因此函数 L ( α ) \mathcal L(\alpha) L(α)的斜率存在:
关于 [ ∇ f ( x k ) ] T P k < 0 [\nabla f(x_k)]^T \mathcal P_k < 0 [∇f(xk)]TPk<0详见优化算法——下降方向的推导过程
- 上界: 0 0 0(无法取到),此时 L ( α ) \mathcal L(\alpha) L(α)的函数图像与 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)的函数图像重合;
- 下界: [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk(无法取到),此时 L ( α ) \mathcal L(\alpha) L(α)的函数图像与 l ( α ) l(\alpha) l(α)的函数图像重合。
对应函数图像表示如下。可以看到:相比上图, α \alpha α轴上绿色实线描述的步长 α \alpha α的选择范围明显小于上图中红色实线描述的范围。从而对最优步长 α \alpha α的选择进行优化。
这里并没有涉及证明过程,仅是从逻辑角度进行描述。

关于为什么要选择 l ( α ) l(\alpha) l(α)的斜率 [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk作为下界的描述 ? ? ?主要是因为:该切线函数在局部范围内的函数图像(凸函数)中不存在位于该切线下方的函数结果。但这仅仅作用于局部范围。因为我们对完整的 ϕ ( α ) \phi(\alpha) ϕ(α)函数未知,在全局范围中可能存在函数信息位于 l ( α ) l(\alpha) l(α)下方。例如下图描述的 ϕ ( α ) \phi(\alpha) ϕ(α)函数:

因此,斜率 [ ∇ f ( x k ) ] T P k [\nabla f(x_k)]^T \mathcal P_k [∇f(xk)]TPk并不是绝对下界。但不否认的是: l ( α ) l(\alpha) l(α)的斜率用于划分有效的 α \alpha α步长来说是苛刻的,至少比 ϕ ( α ) = f ( x k ) \phi(\alpha) = f(x_k) ϕ(α)=f(xk)描述的范围更加严格。
关于 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端
关于 Armijo \text{Armijo} Armijo规则,我们仅从 L ( α ) \mathcal L(\alpha) L(α)公式的角度也能看出它相比 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) <f(x_k) f(xk+1)<f(xk)更加严格:
f ( x k + 1 ) = ϕ ( α ) < L ( α ) = f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ < 0 < f ( x k ) f(x_{k+1}) = \phi(\alpha) < \mathcal L(\alpha) = f(x_k) + \underbrace{\mathcal C_1\cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha}_{<0} <f(x_k) f(xk+1)=ϕ(α)<L(α)=f(xk)+<0 C1⋅[∇f(xk)]TPk⋅α<f(xk)
但 Armijo \text{Armijo} Armijo规则依然存在弊端:在 C 1 ∈ ( 0 , 1 ) \mathcal C_1 \in (0,1) C1∈(0,1)的选择过程中,依然存在:满足 ϕ ( α ) < L ( α ) \phi(\alpha) < \mathcal L(\alpha) ϕ(α)<L(α)的 α \alpha α结果过少,从而这些样本点包含的 α \alpha α范围过小。例如:
其中绿色实线描述 L ( α ) \mathcal L(\alpha) L(α),其对应的有效范围见 α \alpha α轴上的绿色实线。可以看出,覆盖的 α \alpha α范围极小并且对应的 ϕ ( α ) \phi(\alpha) ϕ(α)结果也不够优秀。

上述情况是有可能出现的,虽然我们并不执著最小值一定位于 ϕ ( α ) < L ( α ) \phi(\alpha) < \mathcal L(\alpha) ϕ(α)<L(α)所描述的 α \alpha α范围内(因为是求数值解),但我们同样希望:排除掉类似这种 α \alpha α较小,并且质量不高的情况,或者:我们更希望 ϕ ( α ) \phi(\alpha) ϕ(α)的核心部分有机会出现在范围内。
Glodstein Condition \text{Glodstein Condition} Glodstein Condition
Glodstein Consition \text{Glodstein Consition} Glodstein Consition是在 Armijo Condition \text{Armijo Condition} Armijo Condition的基础上,给 ϕ ( α ) \phi(\alpha) ϕ(α)的范围加上一个下界:
{ Glodstein Condition : f ( x k ) + C 2 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ Lower Bound ≤ ϕ ( α ) ≤ f ( x k ) + C 1 ⋅ [ ∇ f ( x k ) ] T P k ⋅ α ⏟ Upper Bound;Armijo Condition C 1 + C 2 = 1 \begin{cases} \text{Glodstein Condition : }\underbrace{f(x_k) + \mathcal C_2 \cdot [\nabla f(x_k)]^T\mathcal P_k \cdot \alpha}_{\text{Lower Bound}} \leq \phi(\alpha) \leq \underbrace{f(x_k) + \mathcal C_1 \cdot [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha}_{\text{Upper Bound;Armijo Condition}} \\ \quad \\ \mathcal C_1 + \mathcal C_2 = 1 \end{cases} ⎩ ⎨ ⎧Glodstein Condition : Lower Bound f(xk)+C2⋅[∇f(xk)]TPk⋅α≤ϕ(α)≤Upper Bound;Armijo Condition f(xk)+C1⋅[∇f(xk)]TPk⋅αC1+C2=1
经过整理,使用一个参数 C \mathcal C C对上述范围进行描述:
f ( x k ) + ( 1 − C ) [ ∇ f ( x k ) ] T P k ⋅ α ≤ ϕ ( α ) ≤ f ( x k ) + C ⋅ [ ∇ f ( x k ) ] T P k α C ∈ ( 0 , 1 2 ) f(x_k) + (1 - \mathcal C) [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha \leq \phi(\alpha) \leq f(x_k) + \mathcal C \cdot [\nabla f(x_k)]^T \mathcal P_k \alpha \quad \mathcal C \in \left(0,\frac{1}{2}\right) f(xk)+(1−C)[∇f(xk)]TPk⋅α≤ϕ(α)≤f(xk)+C⋅[∇f(xk)]TPkαC∈(0,21)
对应的函数图像表示如下:

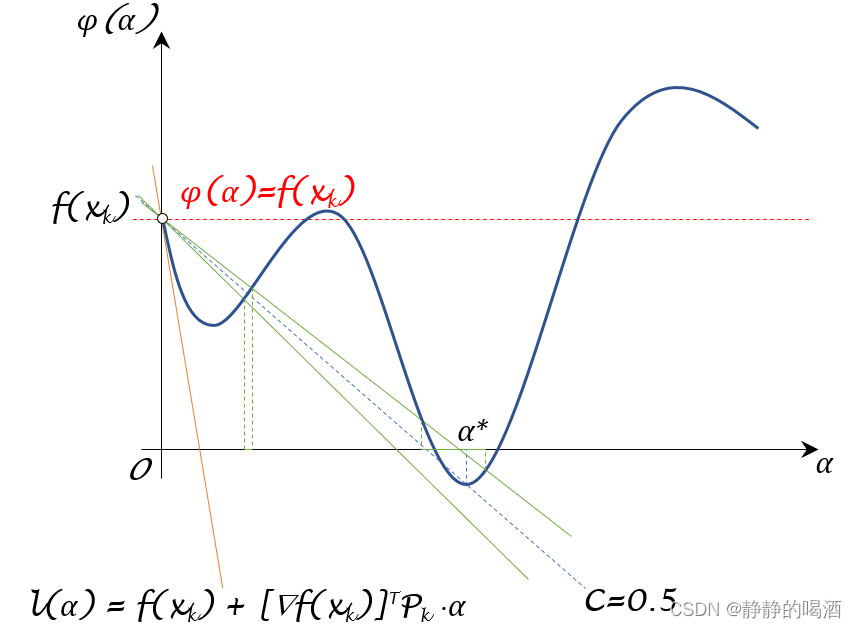
其中两条绿色实线关于 f ( x k ) + 1 2 [ ∇ f ( x k ) ] T P k ⋅ α \begin{aligned}f(x_k) + \frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} f(xk)+21[∇f(xk)]TPk⋅α(蓝色虚线)对称,两条绿色实线之间的范围就是 ϕ ( α ) \phi(\alpha) ϕ(α)有效的选择范围。其对应的 α \alpha α选择范围见上图 α \alpha α轴上的绿色实线。
从而可以通过修改 C \mathcal C C的数值,从而调整上图绿色实线之间的夹角。这种 ϕ ( α ) \phi(\alpha) ϕ(α)的选择方式极大程度地将 ϕ ( α ) \phi(\alpha) ϕ(α)的核心部分包含在选择范围内。从而缓解了 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端。
Goldstein Condition \text{Goldstein Condition} Goldstein Condition的弊端
即便 Goldstein Condition \text{Goldstein Condition} Goldstein Condition缓解了 Armijo Condition \text{Armijo Condition} Armijo Condition的弊端。但其自身也同样存在弊端:当参数 C \mathcal C C接近 1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21时,上下界均会朝着中心轴 f ( x k ) + 1 2 [ ∇ f ( x k ) ] T P k ⋅ α \begin{aligned}f(x_k) + \frac{1}{2} [\nabla f(x_k)]^T \mathcal P_k \cdot \alpha\end{aligned} f(xk)+21[∇f(xk)]TPk⋅α方向靠拢。最终可能得到如下效果:
虽然这里描述的ϕ ( α ) \phi(\alpha) ϕ(α)范围还比较优秀,但这只是特例。在两条绿线之间的夹角极小时,我们映射出的ϕ ( α ) \phi(\alpha) ϕ(α)范围以及对应的α \alpha α范围都非常小,后面可能导致其将一些优质的α \alpha α结果给过滤掉。但与Armijo Condition \text{Armijo Condition} Armijo Condition相比,Goldstein Condition \text{Goldstein Condition} Goldstein Condition确实将选择范围集中在ϕ ( α ) \phi(\alpha) ϕ(α)的核心位置,而不是数量少的,较偏的ϕ ( α ) \phi(\alpha) ϕ(α)位置上。
下一节针对 Glodstein Condition \text{Glodstein Condition} Glodstein Condition因 C \mathcal C C值过于接近 1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21而导致优质 α \alpha α结果被误杀的情况,我们介绍 Wolfe Condition \text{Wolfe Condition} Wolfe Condition。
相关参考:
【优化算法】线搜索方法-步长-Glodstein Condition







)
,floor(),round()函数C++详解)

)






)

