文章目录
- 二叉排序树
- 总览
- 二叉排序树的定义
- 二叉排序树的查找
- 二叉排序树的插入
- 二叉排序树的构造
- 二叉排序树的删除
- 删除的是叶子节点
- 删除的是只有左子树或者只有右子树的节点
- 删除的是有左子树和右子树的节点
- 查找效率分析
- 查找成功
- 查找失败
- 小结
二叉排序树
总览
二叉排序树的定义
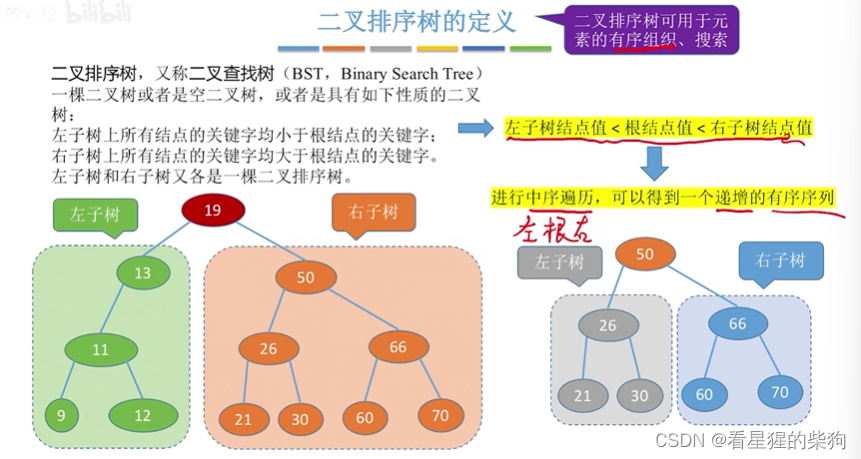
二叉排序树的查找
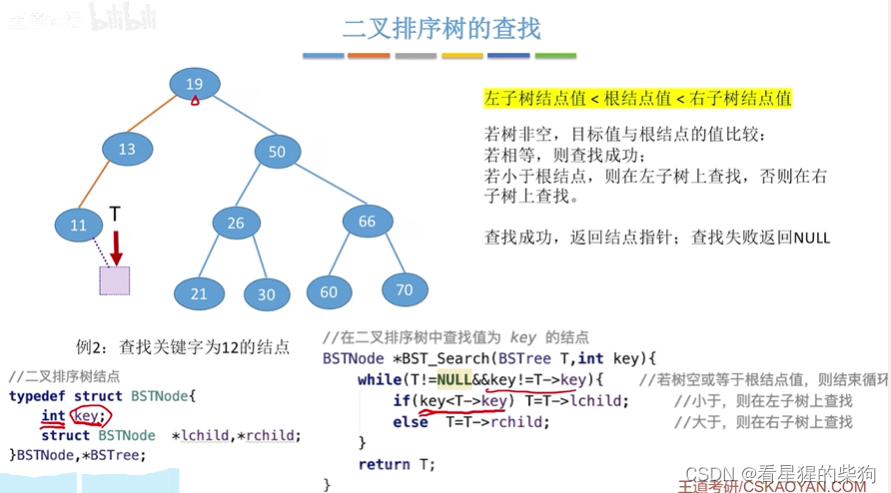
我们也可以用递归实现
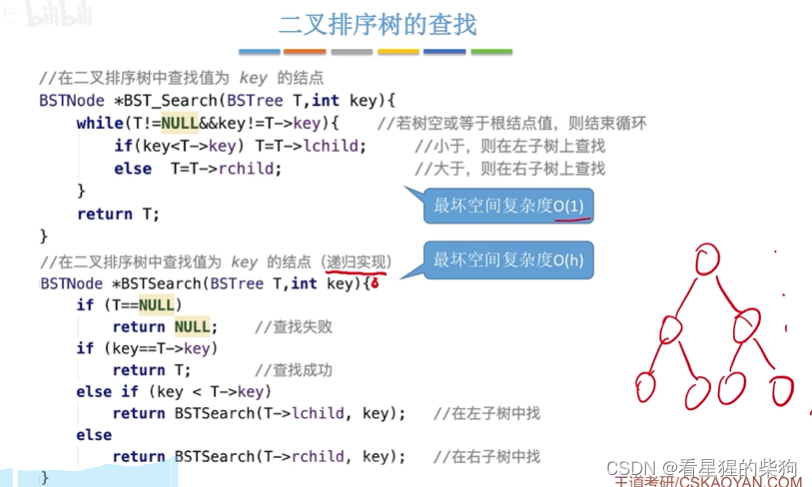
但递归的最坏情况可能需要有h个函数调用栈帧,或者说h个函数同时执行
但循环的实现一直都是一个函数在执行
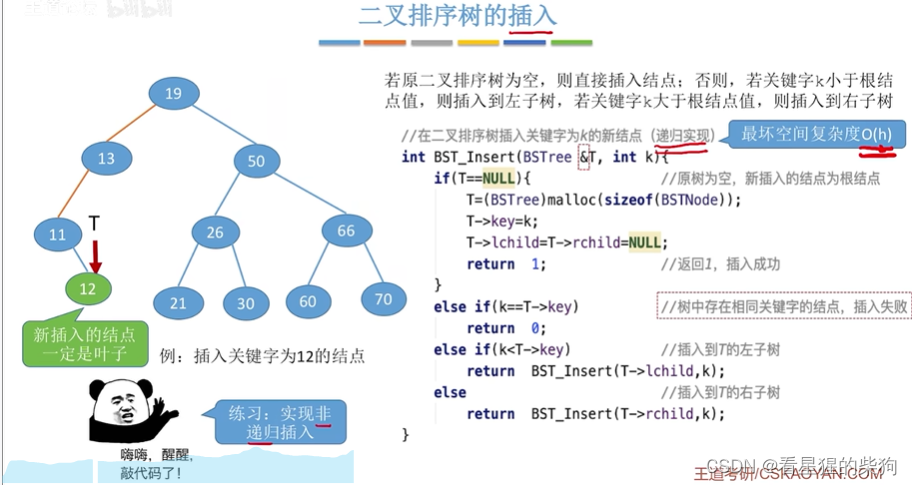
二叉排序树的插入
先查找找到插入的位置,然后mallloc一个新的空间,如果遇到与插入值一样的元素,则插入失败
函数参数是引用类型从而能够修改其值
二叉排序树的构造
首先T是空,会创造一个节点,其值和插入的值一样,这样就开始形成一颗树,接着插入过程和之前一样
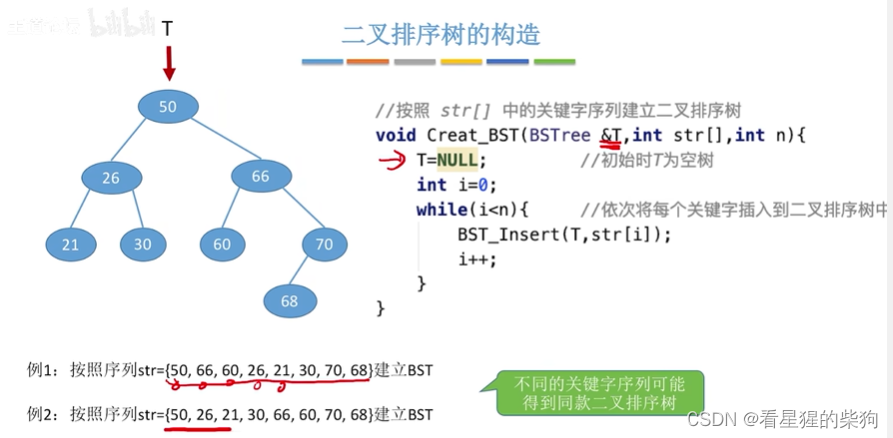
不同序列对应的二叉排序树不一定相同,也不一定不同
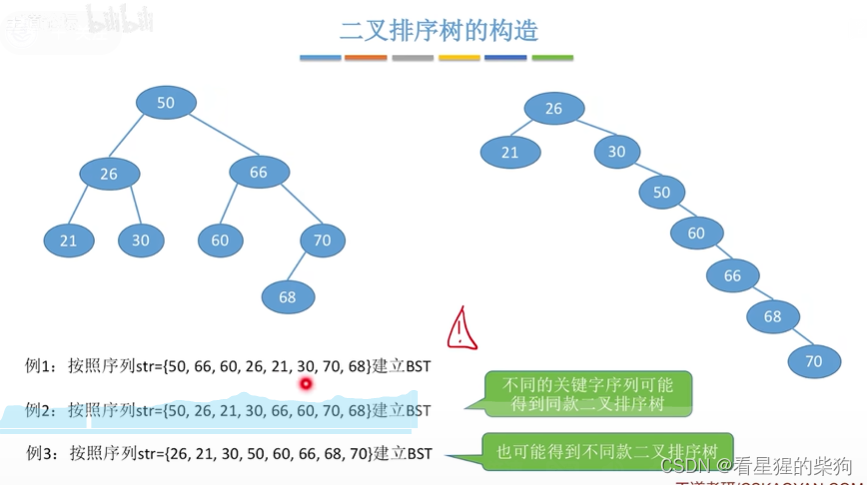
二叉排序树的删除
删除的是叶子节点
直接删之后依然可以保存二叉树的特性
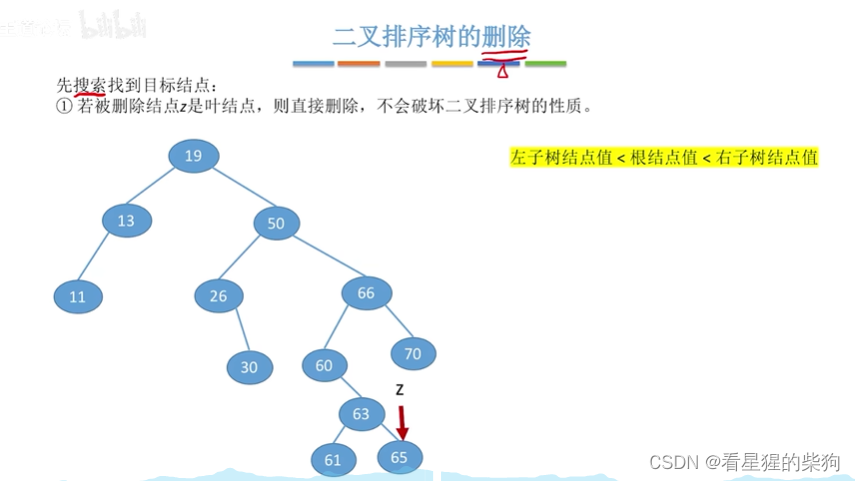
删除的是只有左子树或者只有右子树的节点
直接替代即可,此时依然满足,替换后,子树相对于父父树一定满足父树的相对于其父父树的性质
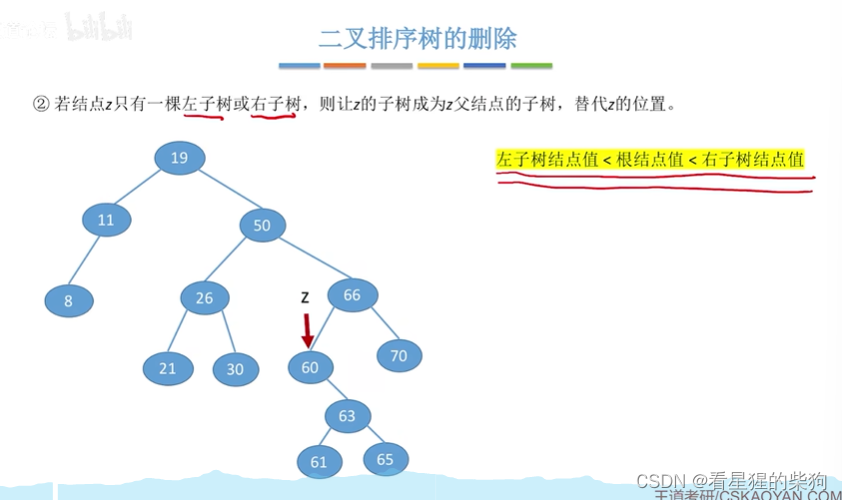
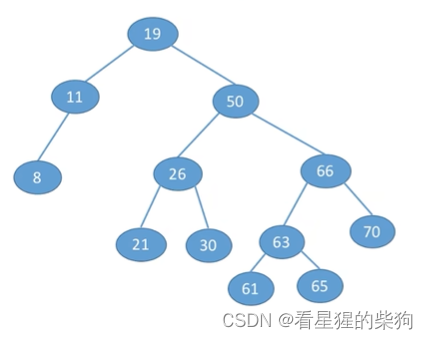
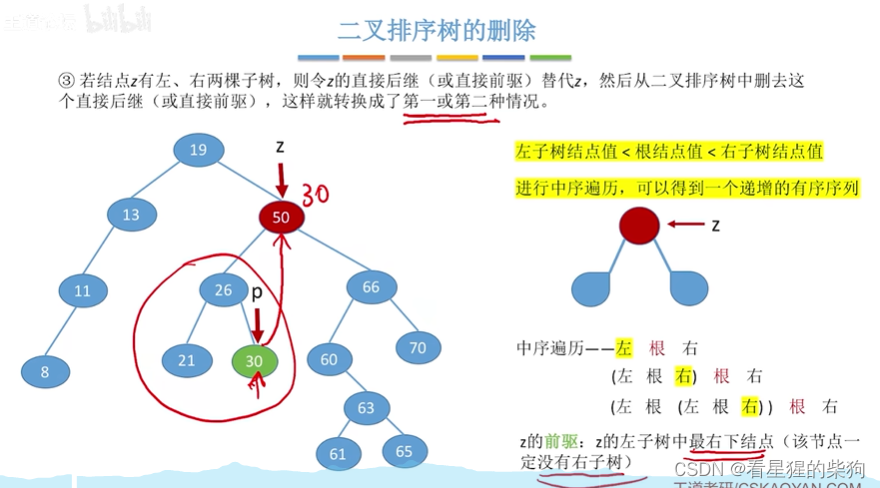
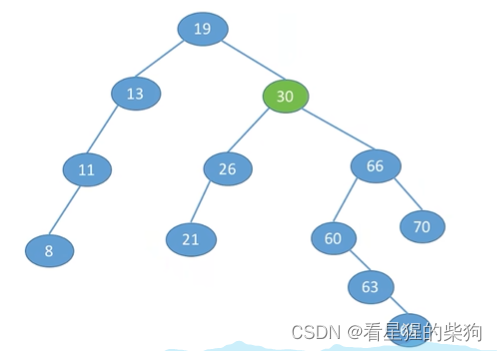
删除的是有左子树和右子树的节点
此时可以找到右子树的最小节点来替换(右子树的最左下节点)
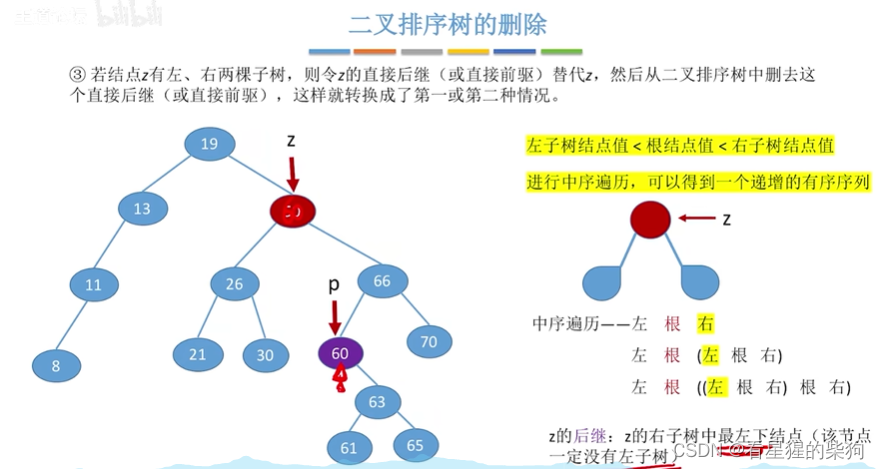
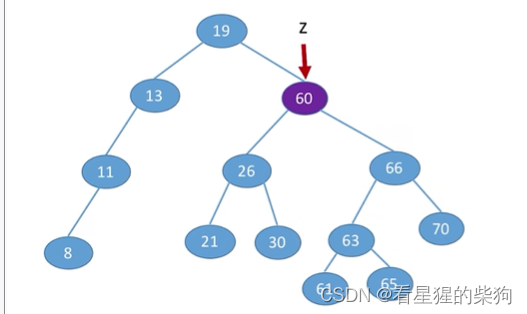
此时可以找到左子树的最大节点来替换(左子树的最右下节点)
查找效率分析
查找成功
最坏的查找长度也是和这颗数的高度一样
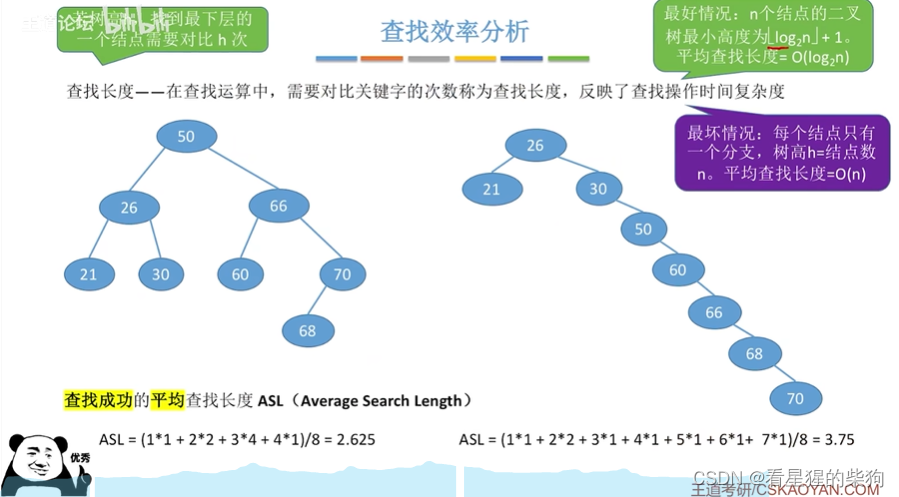
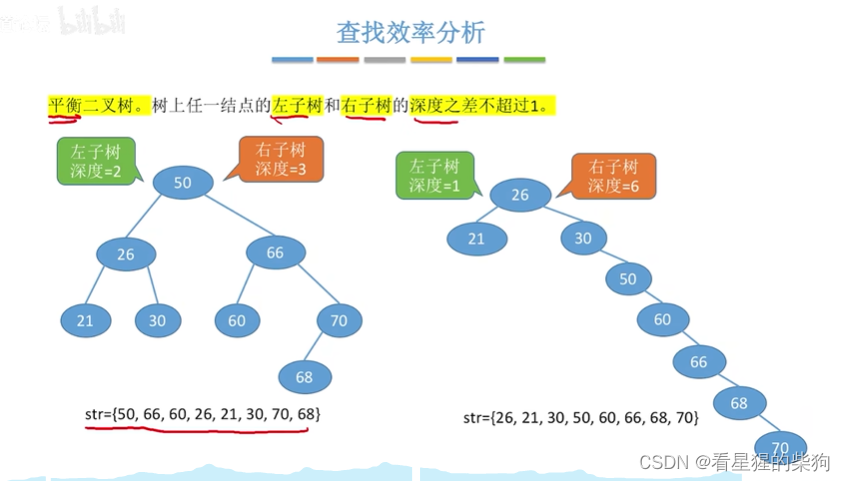
如果使得二叉树的尽可能地平衡,那么二叉树的高度会越低
查找失败
查找失败时为落在空结点的位置,先补齐空结点

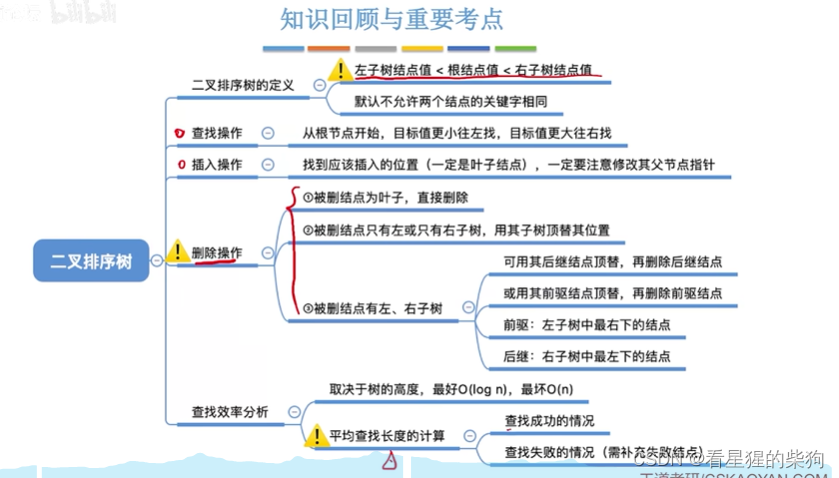
小结















)



