一.线性表

1.定义：

n个同类型数据元素的有限序列，记为

L为表名，i为数据元素在线性表中的位序，n为线性表的表长，n=0时称为空表。

2.数据元素之间的关系：

直接前驱和直接后继

3.抽象数据类型线性表的定义：

ADT List{

数据对象：

数据关系：

一个长度为n的线性表有n-1个数据关系

基本操作：

（1）结构初始化操作

（2）结构销毁操作

（3）访问型操作

（4）加工型操作
}ADTList

二.存储结构

1.顺序存储

以x的存储位置和y的存储位置之间某种关系表示逻辑关系<x,y>

最简单的一种顺序存储方式是：

令y的存储位置和x的存储位置相邻。

用一组地址连续的存储单元依次存放线性表中的数据元素

线性表的起始地址称为线性表的基地址

所有数据元素的存储位置均取决于第一个数据元素的存储位置

1.1 顺序表的定位查找

将顺序表中的元素逐个与给定值e相比较

时间复杂度为

1.2 顺序表的插入操作

插入位置以及之后的元素后移

时间复杂度为

1.3 顺序表的删除操作

删除该元素并且该元素之后的元素前移

时间复杂度为

2.单链表

用一组地址任意的存储单元存放线性表中的数据。

结点（表示数据元素的存储）=元素+地址

结点的序列表示线性表——称作链表

2.1 头结点

为了操作方便，在第一个结点之前虚加一个“头结点”，以指向头结点的指针为链表的头指针。

2.2 访问第i个元素

p=p->next;

时间复杂度为

2.3 在第i个位置插入元素

寻找第i-1个位置

再进行插入

时间复杂度为

 2.4 在第i个位置删除元素

寻找第i-1个位置

再进行删除

时间复杂度为

2.5 将单链表置为空表

时间复杂度为

2.6 如何从线性表中得到单链表？

链表是一个动态的结构，它不需要预先分配空间，因此生成链表的过程是一个结点“逐个插入”的过程。

2.7 其他形式的链表

1）双向链表

有两个指针，一个指向前驱，一个指向后继。

2）循环链表

最后一个结点的指针域的指针又指回第一个结点的链表。

和单链表的差别仅在于：判别链表中最后一个结点的条件不再是“后继是否为空”，而是“后继是否为头结点”。

3）双向循环链表

2.8 双向链表的操作特点

“查询”和单链表相同

“插入”和“删除”时需要同时修改两个方向上的指针。

例如“插入”：

s->next=p->next;

p->next=s;

s->next->prior=s;

s->prior=p;

例如“删除”：

s=p->next;

p->next=p->next->next;

p->next->prior=p;

delete s;

 3.总结

顺序表适合查找操作，而链表适合插入和删除操作。

三.栈（操作受限的线性数据结构）

1.栈的抽象类型定义：

ADT Stack{

数据对象：

数据关系：

约定端为栈顶，端为栈底。

基本操作：

}ADTStack

2.顺序栈

指向表尾的指针可以作为栈顶指针

3.链栈

链栈中指针的方向是从栈顶元素往下指

4.栈的应用举例：

1）数制转换

void conversion(){

    stack <int> s;

    int N;

    cin>>N;

    while(N){

        s.push(N%8);//余数进栈

        N/=8;

    }

    while(!s.empty()){

        cout<<s.top();

        s.pop();

    }

    cout<<endl;

}

2)表达式求值

表达式由操作数、运算符、界限符组成。

操作数（operand）：常数或变量

运算符（operator）：算数、关系、逻辑等

界限符（delimiter）：左右括号、表达式结束符#等

运算符优先表

算法思想：

使用两个栈，一个运算符栈（OPTR）一个操作数栈（OPND）

1）OPND置为空栈，将#放入OPTR栈

2）依次读入表达式中的每个字符

3）若是操作数，读入OPND栈，若是运算符，则和OPTR栈的栈顶元素进行优先级比较，若栈顶元素优先级高，则执行相应运算，结果存入OPND栈；若栈顶元素优先级低，则将该字符读入OPTR栈；若优先级相同，则做‘##’或‘（）’处理。

4）重复上述操作，直到表达式求值完毕（读入的是‘#’，并且OPTR栈顶元素也为‘#’）

3）迷宫求解

回溯法：一种不断试探且及时纠正错误的搜索方法。

回溯法思想：从入口出发，按某一方向向前探索，若能走通（未走过），则到达新点，否则试探下一没有探索过的方向，若所有的方向均没有通路，则沿原点返回前一点，换下一个方向再继续试探，直到所有可能的通路都探索过，或找到一条通路，或无路可走又返回到入口点。

（1）表示迷宫的数据结构

#define M 6        //迷宫的实际行和列

#define N 8

int maze[M+2][N+2];

入口坐标为（1，1），出口坐标为（M，N）

（2）试探方向

每个点有8个方向可以试探，试探顺序规定为：从正东方向顺时针方向进行。

move数组定义

typedef struct{
int x,y;

}item;

item move[8];

x:行坐标增量

y:列坐标增量

（3）栈的设计

当到达了某点而无路可走时需要返回前一点，再从前一点开始向下一个方向继续试探。因此，压入栈中的不仅是顺序到达的各点的坐标，而且还要有从看一点到达本点的方向。

栈中元素是一个由行、列、方向组成的三元组。

typedef struct{
int x,y,direction;

}datatype;

栈的定义为：

stack <datatype> s;

（4）如何防止重复到达某点，以避免发生死循环？

当到达某点（i，j）时，将maze[i][j]置为-1

（5）迷宫求解算法思想

1.栈初始化

2.将入口点坐标以及到达该点的方向direction设置为-1，入栈。

3.while（栈不为空）

{

弹栈

求出下一个要试探的方向direction++

while(还有剩余试探方向时){

if(direction方向可走){

则{x,y,direction}入栈，求新点坐标（i，j）

将新点（i，j）切换为当前点（x，y）

if（（x，y）==（M，N））{

结束

                }

else{

重制direction=0；

}

}

else

direction++;

}

}

四.队列

1.队列的抽象定义

ADT Queue{

数据对象：

数据关系：

约定：其中端为队列头，端为队列尾。

基本操作：

}ADT Queue

2.顺序队列

#define MAXQSIZE 100
typedef struct{
ElemType base[MAXQSIZE];
int front;//头指针，若队列不为空，指向队列头元素
int resr;//尾指针，若队列不为空，指向队列尾元素的下一个位置
}SqQueue;

2.1 "假溢出"

为了解决假溢出问题，采用循环队列。

队满和队空时均有sq.front==sq.rear

无法判断队满还是队空。

1）方法一：

用一个计数变量来记录队列中元素的个数。

2）方法二：

设置一个标志位。

当有元素入队时，标志位为true；有元素出队时，标志位为false。

3）方法三：

牺牲一个元素空间，来区别队空或队满。 

队满：(sq.rear+1)%queue_length==sq.front

队空：sq.front==sq.rear

2.2 插入元素e为Q的新的队尾元素

1）判断队列是否满

2）满了，则error

3）没满，Q.base[Q.rear]=e;

Q.rear=(Q.rear+1)%queue_length;

2.3 出队

1）判断队列是否为空

2）空，返回error

3）非空，e=Q.base[Q.front];

Q.front=(Q.front+1)%queue_length;

2.4 队列长度 

return ((Q.rear-Q.front+queue_length)%queue_length);

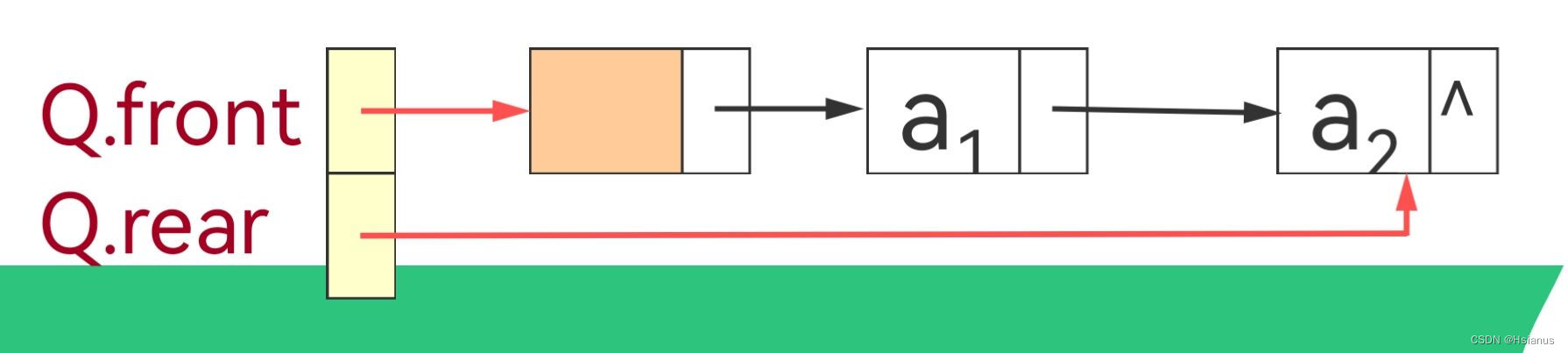
3.链队列

typedef struct QNode{
QelemType data;
struct QNode *next;}*QueuePtr;

typedef struct{
QueuePtr front;
QueuePtr rear;
}LinkQueue;

3.1 插入元素e为Q的队尾元素

p=new QNode;

p->data=e;

p->next=NULL;

Q.rear->next=p;

Q.rear=p; 

3.2 出队

if(Q.front==Q.rear)

        return error;

p=Q.front->next;

e=p->data;

Q.front->next=p->next;

if(Q.rear==p)

        Q.rear=Q.front;//避免尾指针成为野指针

delete p;

3.3 构造函数

Q.front=Q.rear=new QNode;

Q.front->next=NULL;//带头结点