在处理机器学习或深度学习问题时，损失/成本函数用于在训练期间优化模型。目标几乎总是最小化损失函数。损失越低，模型越好。交叉熵损失是最重要的成本函数。它用于优化分类。对交叉熵的理解取决于对 Softmax 激活函数的理解。

 一、softmax激活函数

激活函数是神经网络的组成部分。如果没有激活函数，神经网络是一个简单的线性回归模型。这意味着激活函数为神经网络提供了非线性。

维基百科：通常作为神经网络的最后一层，将网络的输出标准化为预测输出类别的概率分布。

在这里，Z 表示输出层神经元的值，指数充当非线性函数。随后将这些值除以指数值之和以进行标准化，然后将其转换为概率。

例子：

假设 Z21、Z22、Z23 的值分别为 2.33、-1.46 和 0.56。SoftMax 激活函数应用于每个神经元，并生成以下值。

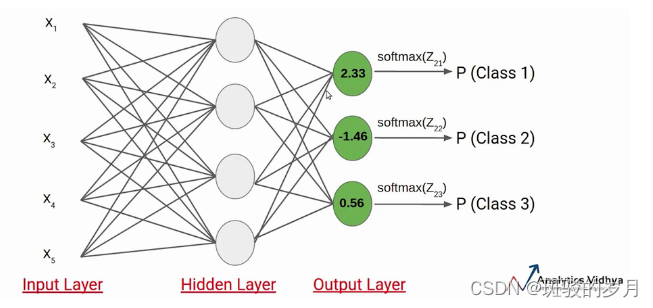
这些是数据点属于各个类别的概率值，各类别概率之和等于 1。

在这种情况下，很明显输入属于类别 1。因此，如果这些类别中任何一个的概率发生变化，第一类的概率值也会发生变化。

二、交叉熵

交叉熵是给定随机变量或事件集的两个概率分布之间差异的度量。

信息量化了编码和传输事件所需的位数。较低概率的事件具有更多的信息，较高概率的事件具有较少的信息。

在信息论中，我们喜欢描述事件的“惊喜”。事件的可能性越小，就越令人惊讶，这意味着它包含更多信息。

• 低概率事件（令人惊讶）：更多信息。
• 高概率事件（不足为奇）：信息较少。

给定事件P(x)的概率，可以计算事件x的信息h(x )如下：

h(x) = -log(P(x))

在物理学中，“熵”被用来表示热力学系统所呈现的无序程度。香农将这一概念引入信息论领域，提出了“信息熵”概念，通过对数函数来测量信息的不确定性。

交叉熵（cross entropy）是信息论中的重要概念，主要用来度量两个概率分布间的差异。假定 p和 q是数据 x的两个概率分布，通过 q来表示 p的交叉熵可如下计算：

交叉熵刻画了两个概率分布之间的距离，旨在描绘通过概率分布 q来表达概率分布 p的困难程度。根据公式不难理解，交叉熵越小，两个概率分布 p和 q越接近。这里仍然以三类分类问题为例，假设数据 x属于类别 1。记数据x的类别分布概率为 y，显然 y=(1,0,0)代表数据 x的实际类别分布概率。记代表模型预测所得类别分布概率。那么对于数据 x而言，其实际类别分布概率 y和模型预测类别分布概率的交叉熵损失函数定义为：

神经网络所预测类别分布概率与实际类别分布概率之间的差距越小越好，即交叉熵越小越好。

交叉熵的定义是基于信息论的思想，通过使用一个概率分布的负对数来表示事件的信息量，然后在另一个概率分布下计算这些信息量的平均值。这使得交叉熵成为衡量两个概率分布差异的一种有效方式，尤其在机器学习中，它经常被用作分类问题的损失函数。

假设所预测中间值 (z1,z2,z3)经过 Softmax映射后所得结果为 (0.34,0.46,0.20)。由于已知输入数据 x属于第一类，显然这个输出不理想而需要对模型参数进行优化。如果选择交叉熵损失函数来优化模型，则 (z1,z2,z3)这一层的偏导值为 (0.34−1,0.46,0.20)=(−0.66,0.46,0.20)。

可以看出，softmax和交叉熵损失函数相互结合，为偏导计算带来了极大便利。偏导计算使得损失误差从输出端向输入端传递，来对模型参数进行优化。在这里，交叉熵与Softmax函数结合在一起，因此也叫softmax损失（Softmax with cross-entropy loss）。