大数运算·字符串相加·阶乘

在这里插入图片描述
大数，就是C/C++中利用基本类型所不能存储的数字，少则数十位，大则几万位，如何存储和计算大数就是本文的内容。

在C和C++中，没有存储大数的数据结构，就算 unsigned long long也只能表示19位的数字
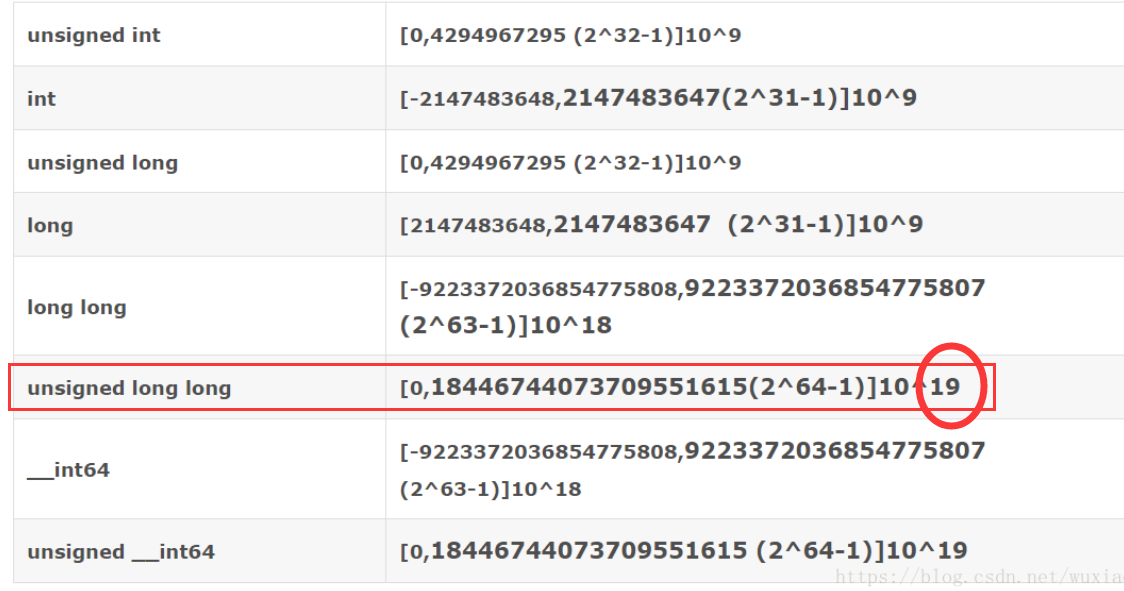
在这里插入图片描述
如果我们用double则会出现精度不准确的问题，如果我们想精确储存计算大数，学习本文是必要的。
存储大数的方法有两种，不管是数组还是字符串，在运算时他们的原理其实是相同的。
看下边两道题，带你了解大数的计算方法

字符串相加
在这里插入图片描述

这道题的思路很简单，不能将字符串转换为整数形式，就算转了我们也过不了这道题。因为数据的范围很大。

长度为一万的数字字符串，这就是一个很大的数了。
解决思路：还记得我们小学时是如何进行加法运算的吗？我们从地位算起，如果两个加数和大于10，我们就会进一，按照这种思路依次进行计算，知道求出结果为止。
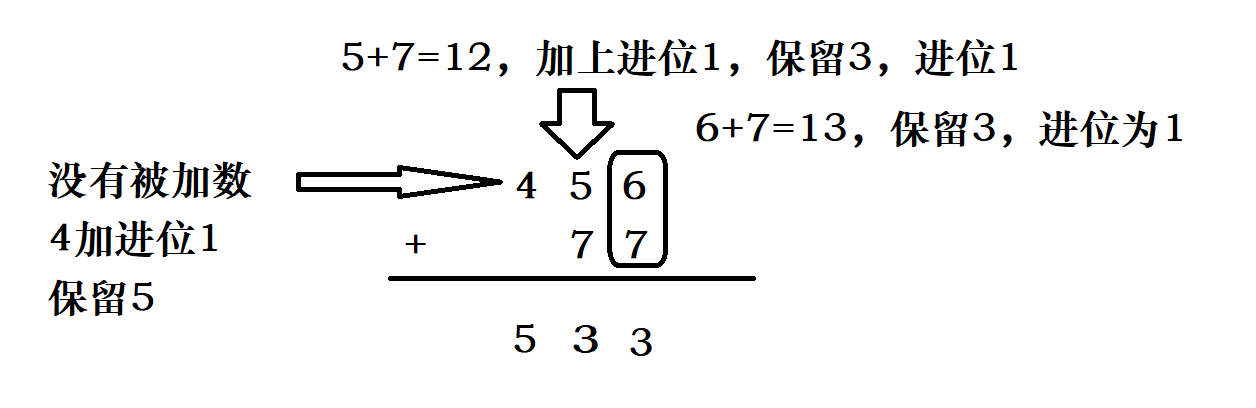
在这里插入图片描述
通过这种思路我们可以写出这样的代码

class Solution {
public:string addStrings(string num1, string num2) {int i = num1.length() - 1, j = num2.length() - 1, add = 0;string ans = "";while (i >= 0 || j >= 0) {int x = i >= 0 ? num1[i] - '0' : 0;int y = j >= 0 ? num2[j] - '0' : 0;int result = x + y + add;ans.insert(ans.begin(),'0' + result % 10);add = result / 10;i -= 1;j -= 1;}return ans;}
};

可以看出，计算时是从字符串末尾一次项前进行求和计算。如果该数大于10，就会将进位更新为1,改为的结果直接将相加后的值模上10的计算结果头插进去即可。
在这里插入图片描述

三目运算符十分巧妙，在求和时，要一直将两数组的元素全部加一遍，如果短的数组已经加完就作为0，这样也不会出现越界访问，还解决了要判断是哪个数组更短的问题，统一对待。在每次对应位计算完成之后更新add（进位数）。然后继续加进位的数字。
信心满满提交
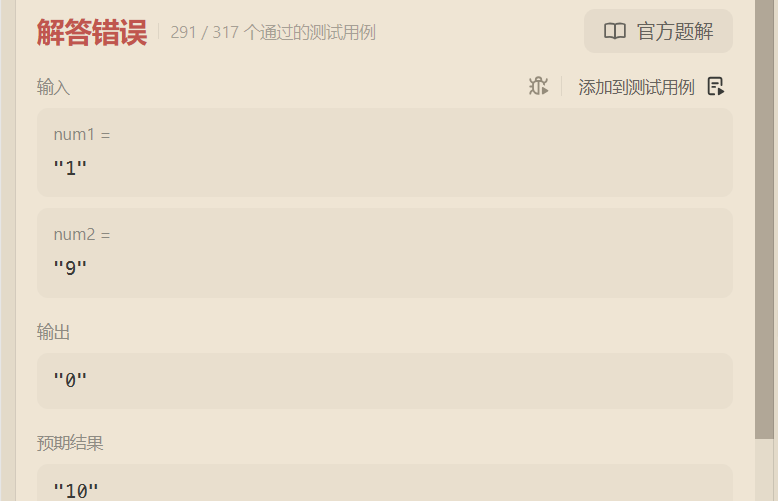
在这里插入图片描述
最后一次进位的情况被我们忽略了，就像上边的错误用例一样。所以当i和j全部减到零，并且进位add也等于0时循环结束。

class Solution {
public:string addStrings(string num1, string num2) {int i = num1.length() - 1, j = num2.length() - 1, add = 0;string ans = "";while (i >= 0 || j >= 0 || add != 0) {int x = i >= 0 ? num1[i] - '0' : 0;int y = j >= 0 ? num2[j] - '0' : 0;int result = x + y + add;//该位置上两个数字求和结果ans.insert(ans.begin(),'0' + result % 10);add = result / 10;i -= 1;//向前一位进发j -= 1;}return ans;}
};

这道题就完成了。
就算两个字符串很长很长，计算也很快，结果也是准确的。
在这里插入图片描述

用数组进行存储运算

用数组存储的话，要保证数组中任意元素不大于10，这才是无误的存储方法，如果某个元素大于10，那就全乱了，一般请况下我们都是用数组进行存储大数操作，而不是计算。就算是要计算的话还要给你提供每个元素都是小于10的数字，用上边字符串的思路进行计算就可以了。

存储大数，一般是通过数组保存运算后很大的数字。
例如求某数的阶乘
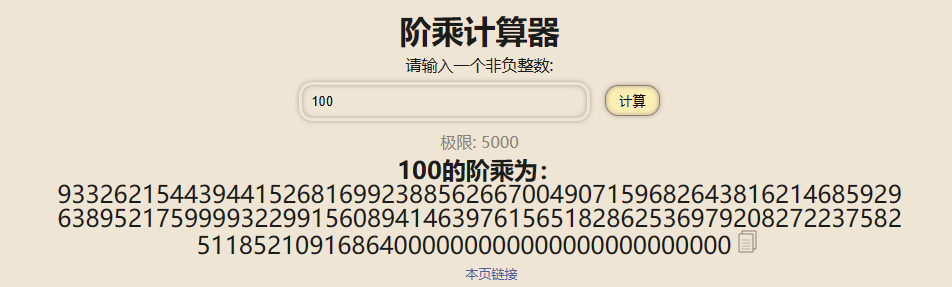
在这里插入图片描述
100的阶乘long long就已经受不了了，那么如何进行精确计算呢？
还是回忆小学时候我们如何计算乘法的呢？

上边的字符串相加的题目中，我们可以发现进位add只有两种，0或者1，因为就算两个9相加，结果也还是18，进位仍然是1，在这里就不同了。
我们可以把99*99看做在数组中保存的两个9分别乘以99，他们在数组中的位置表示他们的位数。
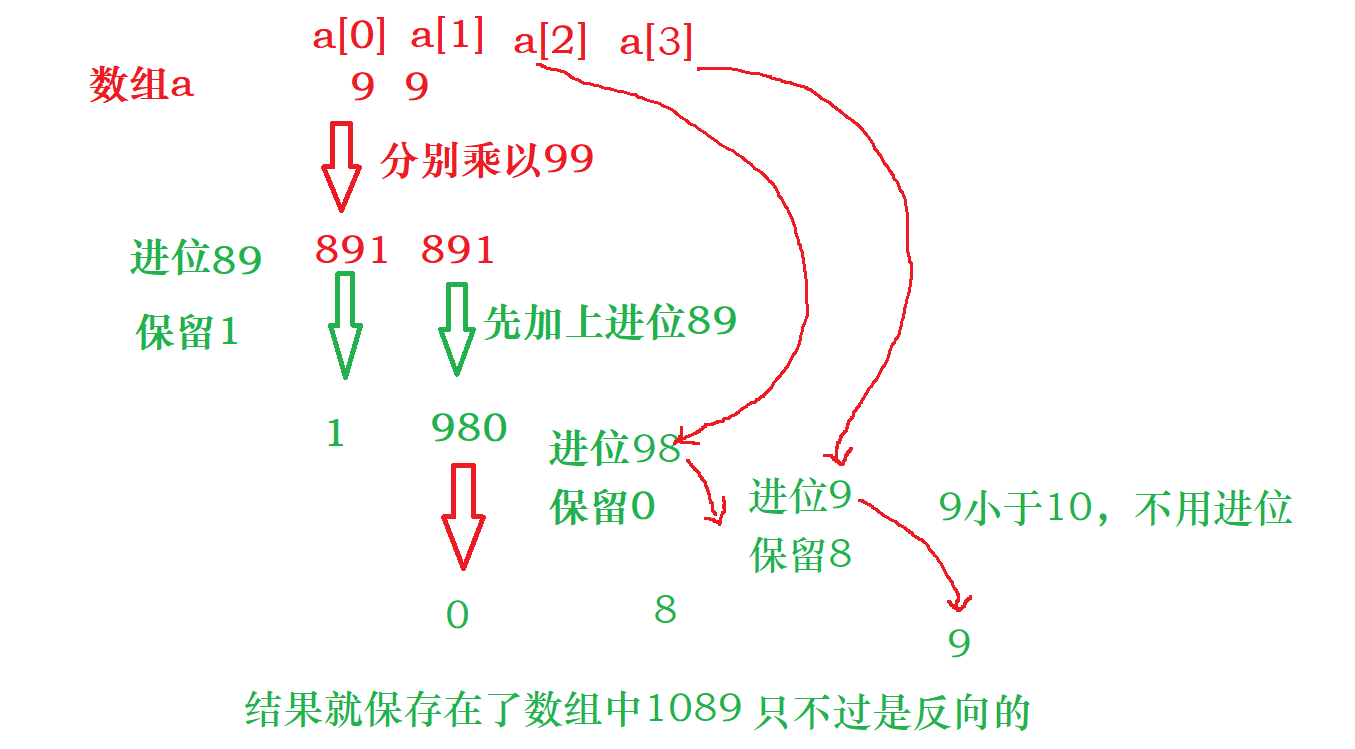
在这里插入图片描述
如果是求阶乘的话，就是要将两个数字相乘之后的数字再乘以一个数而已，同样的思路，多了一层循环。
就像上边，再乘以98的话，就是数组中每一位的数字都乘以98，然后重复上边的操作就可以了。在乘以下一个数之前，要知道上一次乘完的结果的位数，起始时可以将计算的第一个数字乘以1，然后判断出位数，再次运算时就使数组中每一位的数字乘以要乘以的数字。
例如100的阶乘，让数组中首元素为1，第一次运算完成之后数组中前三个元素就是0，0，1，有三位数字，位数为cout=3。然后乘以99，就是数组中前三个元素乘以99，前两个数字不变，最后的数字是大于10的，在进位结束后，判断数组下标为2（一共3位数字，最后一位下标为2）的位置是否大于10，如果大于就进位，此时需要进位一个9，同时位数cout加1，当然，这是一个循环，如果最后一位乘的数不是99而是101，就要进位两次，第一次进位10，第二次进位1，当然位数就要加2。
有了上边的思路就可以写代码了

int main()
{int num = 0;scanf("%d", &num);if (num == 0){printf("1");}int a[10000] = { 0 };a[0] = 1;int cout = 1;//分为三步处理for (int i = num; i > 0; i--){int j = 0;//cout是位数，将所有的位数都乘以i。for (; j < cout; j++){a[j] *= i;}//将每个位判断一下，如果大于等于10，就向前进位for (int k = 0; k < cout; k++){if (a[k] >= 10){a[k + 1] += a[k] / 10;a[k] = a[k] % 10;}}//从最后一位进行判断，找到新的位数for (int l = cout; a[l] >0; l++){cout++;a[l + 1] = a[l] / 10;a[l] = a[l] % 10;}		}for (int i = cout-1; i >0; i--)//从后向前遍历打印{printf("%d ", a[i]);}return 0;
}