1.反向传播算法(BP)的概念及简单推导
反向传播(Backpropagation,BP)算法是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见算法。BP算法对网络中所有权重计算损失函数的梯度,并将梯度反馈给最优化方法,用来更新权值以最小化损失函数。该算法会先按前向传播方式计算(并缓存)每个节点的输出值,然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。
接下来我们以全连接层,使用sigmoid激活函数,Softmax+MSE作为损失函数的神经网络为例,推导BP算法逻辑。由于篇幅限制,这里只进行简单推导,后续Rocky将专门写一篇PB算法完整推导流程,大家敬请期待。
首先,我们看看sigmoid激活函数的表达式及其导数:
s i g m o i d 表达式: σ ( x ) = 1 1 + e − x sigmoid表达式:\sigma(x) = \frac{1}{1+e^{-x}} sigmoid表达式:σ(x)=1+e−x1
s i g m o i d 导数: d d x σ ( x ) = σ ( x ) − σ ( x ) 2 = σ ( 1 − σ ) sigmoid导数:\frac{d}{dx}\sigma(x) = \sigma(x) - \sigma(x)^2 = \sigma(1- \sigma) sigmoid导数:dxdσ(x)=σ(x)−σ(x)2=σ(1−σ)
可以看到sigmoid激活函数的导数最终可以表达为输出值的简单运算。
我们再看MSE损失函数的表达式及其导数:
M S E 损失函数的表达式: L = 1 2 ∑ k = 1 K ( y k − o k ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{k=1}(y_k - o_k)^2 MSE损失函数的表达式:L=21k=1∑K(yk−ok)2
其中 y k y_k yk 代表ground truth(gt)值, o k o_k ok 代表网络输出值。
M S E 损失函数的偏导: ∂ L ∂ o i = ( o i − y i ) MSE损失函数的偏导:\frac{\partial L}{\partial o_i} = (o_i - y_i) MSE损失函数的偏导:∂oi∂L=(oi−yi)
由于偏导数中单且仅当 k = i k = i k=i 时才会起作用,故进行了简化。
接下来我们看看全连接层输出的梯度:
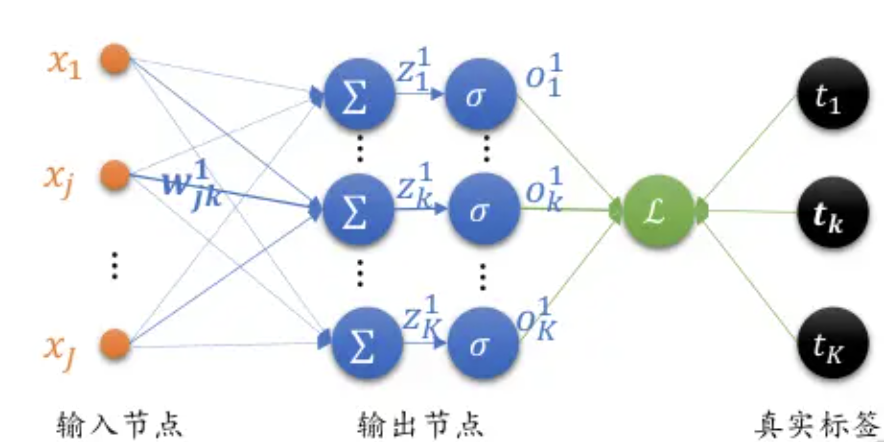
M S E 损失函数的表达式: L = 1 2 ∑ i = 1 K ( o i 1 − t i ) 2 MSE损失函数的表达式:L = \frac{1}{2}\sum^{K}_{i=1}(o_i^1 - t_i)^2 MSE损失函数的表达式:L=21i=1∑K(oi1−ti)2
M S E 损失函数的偏导: ∂ L ∂ w j k = ( o k − t k ) o k ( 1 − o k ) x j MSE损失函数的偏导:\frac{\partial L}{\partial w_{jk}} = (o_k - t_k)o_k(1-o_k)x_j MSE损失函数的偏导:∂wjk∂L=(ok−tk)ok(1−ok)xj
我们用 δ k = ( o k − t k ) o k ( 1 − o k ) \delta_k = (o_k - t_k)o_k(1-o_k) δk=(ok−tk)ok(1−ok) ,则能再次简化:
M S E 损失函数的偏导: d L d w j k = δ k x j MSE损失函数的偏导:\frac{dL}{dw_{jk}} = \delta_kx_j MSE损失函数的偏导:dwjkdL=δkxj
最后,我们看看那PB算法中每一层的偏导数:

输出层:
∂ L ∂ w j k = δ k K o j \frac{\partial L}{\partial w_{jk}} = \delta_k^K o_j ∂wjk∂L=δkKoj
δ k K = ( o k − t k ) o k ( 1 − o k ) \delta_k^K = (o_k - t_k)o_k(1-o_k) δkK=(ok−tk)ok(1−ok)
倒数第二层:
∂ L ∂ w i j = δ j J o i \frac{\partial L}{\partial w_{ij}} = \delta_j^J o_i ∂wij∂L=δjJoi
δ j J = o j ( 1 − o j ) ∑ k δ k K w j k \delta_j^J = o_j(1 - o_j) \sum_{k}\delta_k^Kw_{jk} δjJ=oj(1−oj)k∑δkKwjk
倒数第三层:
∂ L ∂ w n i = δ i I o n \frac{\partial L}{\partial w_{ni}} = \delta_i^I o_n ∂wni∂L=δiIon
δ i I = o i ( 1 − o i ) ∑ j δ j J w i j \delta_i^I = o_i(1 - o_i) \sum_{j}\delta_j^Jw_{ij} δiI=oi(1−oi)j∑δjJwij
像这样依次往回推导,再通过梯度下降算法迭代优化网络参数,即可走完PB算法逻辑。
2.滑动平均的相关概念
滑动平均(exponential moving average),或者叫做指数加权平均(exponentially weighted moving avergae),可以用来估计变量的局部均值,使得变量的更新与一段时间内的历史取值有关。
变量 v v v 在 t t t 时刻记为 v t v_{t} vt , θ t \theta_{t} θt 为变量 v v v 在 t t t 时刻训练后的取值,当不使用滑动平均模型时 v t = θ t v_{t} = \theta_{t} vt=θt ,在使用滑动平均模型后, v t v_{t} vt 的更新公式如下:

上式中, β ϵ [ 0 , 1 ) \beta\epsilon[0,1) βϵ[0,1) 。 β = 0 \beta = 0 β=0 相当于没有使用滑动平均。
t t t 时刻变量 v v v 的滑动平均值大致等于过去 1 / ( 1 − β ) 1/(1-\beta) 1/(1−β) 个时刻 θ \theta θ 值的平均。并使用bias correction将 v t v_{t} vt 除以 ( 1 − β t ) (1 - \beta^{t}) (1−βt) 修正对均值的估计。
加入Bias correction后, v t v_{t} vt 和 v b i a s e d t v_{biased_{t}} vbiasedt 的更新公式如下:

当 t t t 越大, 1 − β t 1 - \beta^{t} 1−βt 越接近1,则公式(1)和(2)得到的结果( v t v_{t} vt 和 v b i a s e d 1 v_{biased_{1}} vbiased1 )将越来越接近。
当 β \beta β 越大时,滑动平均得到的值越和 θ \theta θ 的历史值相关。如果 β = 0.9 \beta = 0.9 β=0.9 ,则大致等于过去10个 θ \theta θ 值的平均;如果 β = 0.99 \beta = 0.99 β=0.99 ,则大致等于过去100个 θ \theta θ 值的平均。
下图代表不同方式计算权重的结果:
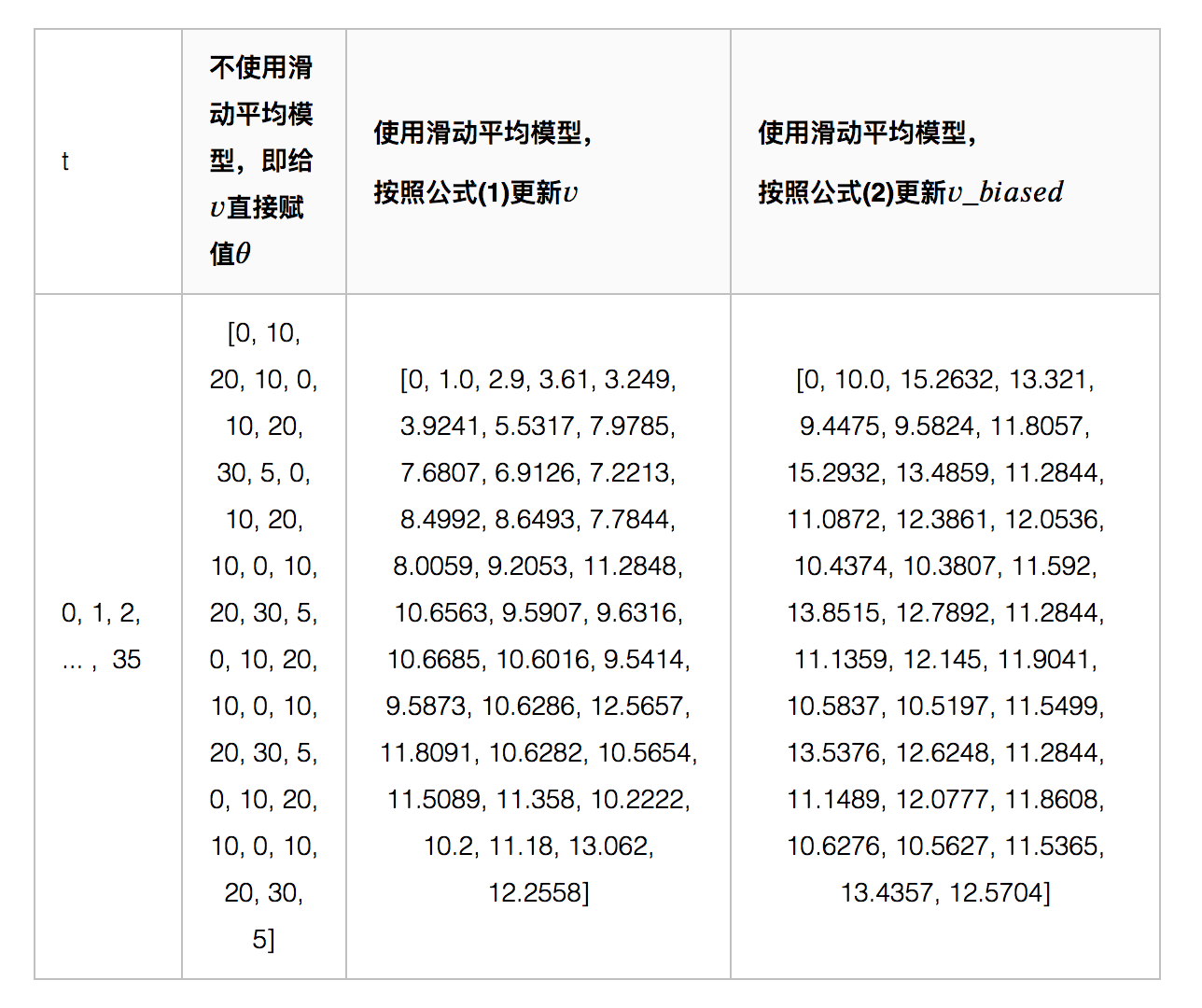
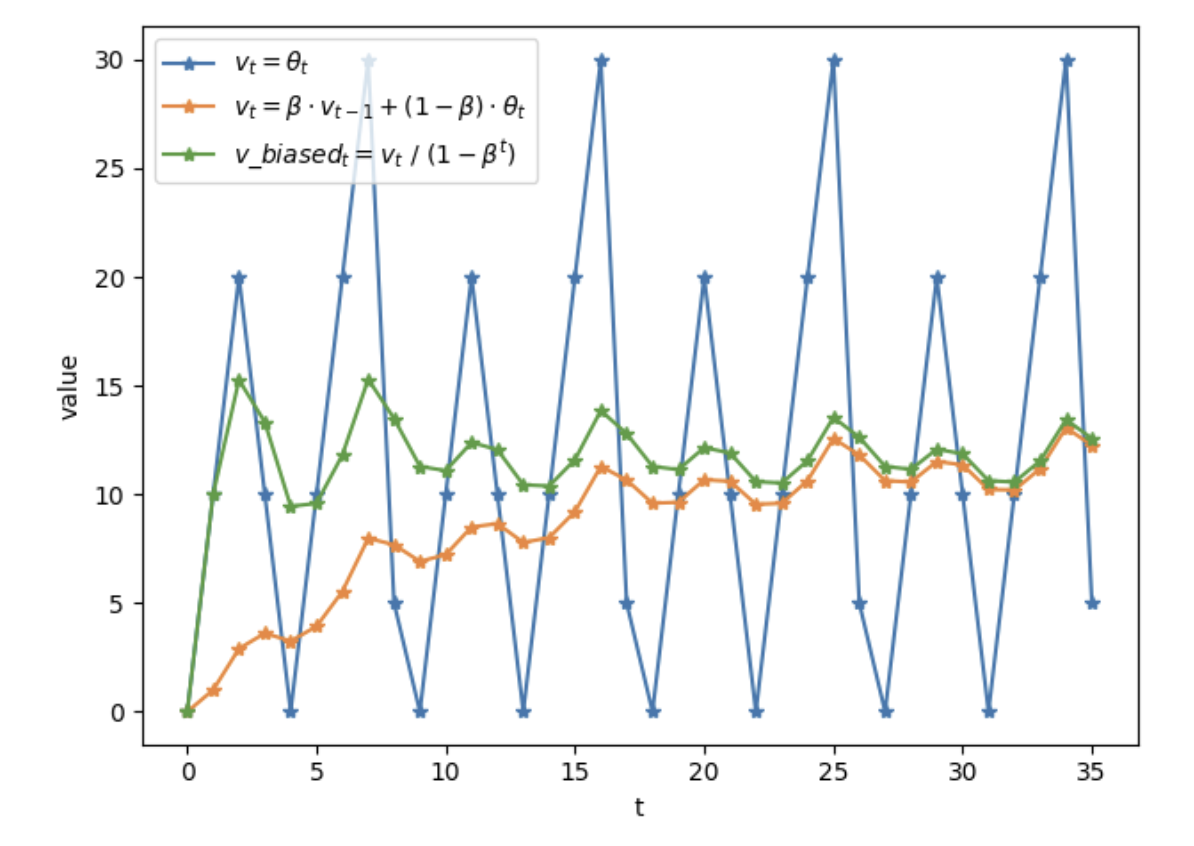
如上图所示,滑动平均可以看作是变量的过去一段时间取值的均值,相比对变量直接赋值而言,滑动平均得到的值在图像上更加平缓光滑,抖动性更小,不会因为某种次的异常取值而使得滑动平均值波动很大。
滑动平均的优势: 占用内存少,不需要保存过去10个或者100个历史 θ \theta θ 值,就能够估计其均值。滑动平均虽然不如将历史值全保存下来计算均值准确,但后者占用更多内存,并且计算成本更高。
为什么滑动平均在测试过程中被使用?
滑动平均可以使模型在测试数据上更鲁棒(robust)。
采用随机梯度下降算法训练神经网络时,使用滑动平均在很多应用中都可以在一定程度上提高最终模型在测试数据上的表现。
训练中对神经网络的权重 w e i g h t s weights weights 使用滑动平均,之后在测试过程中使用滑动平均后的 w e i g h t s weights weights 作为测试时的权重,这样在测试数据上效果更好。因为滑动平均后的 w e i g h t s weights weights 的更新更加平滑,对于随机梯度下降而言,更平滑的更新说明不会偏离最优点很远。比如假设decay=0.999,一个更直观的理解,在最后的1000次训练过程中,模型早已经训练完成,正处于抖动阶段,而滑动平均相当于将最后的1000次抖动进行了平均,这样得到的权重会更加鲁棒。





)


 ))







管理系统标题和logo修改)


