前言:
这b题费了我一身牛劲,结果还是没有做出来,晚上请教大佬后,知晓方法,才将其ac,于是决心务必再次使用传说中的费曼学习法,并与大家分享一下这道题目。
题目:
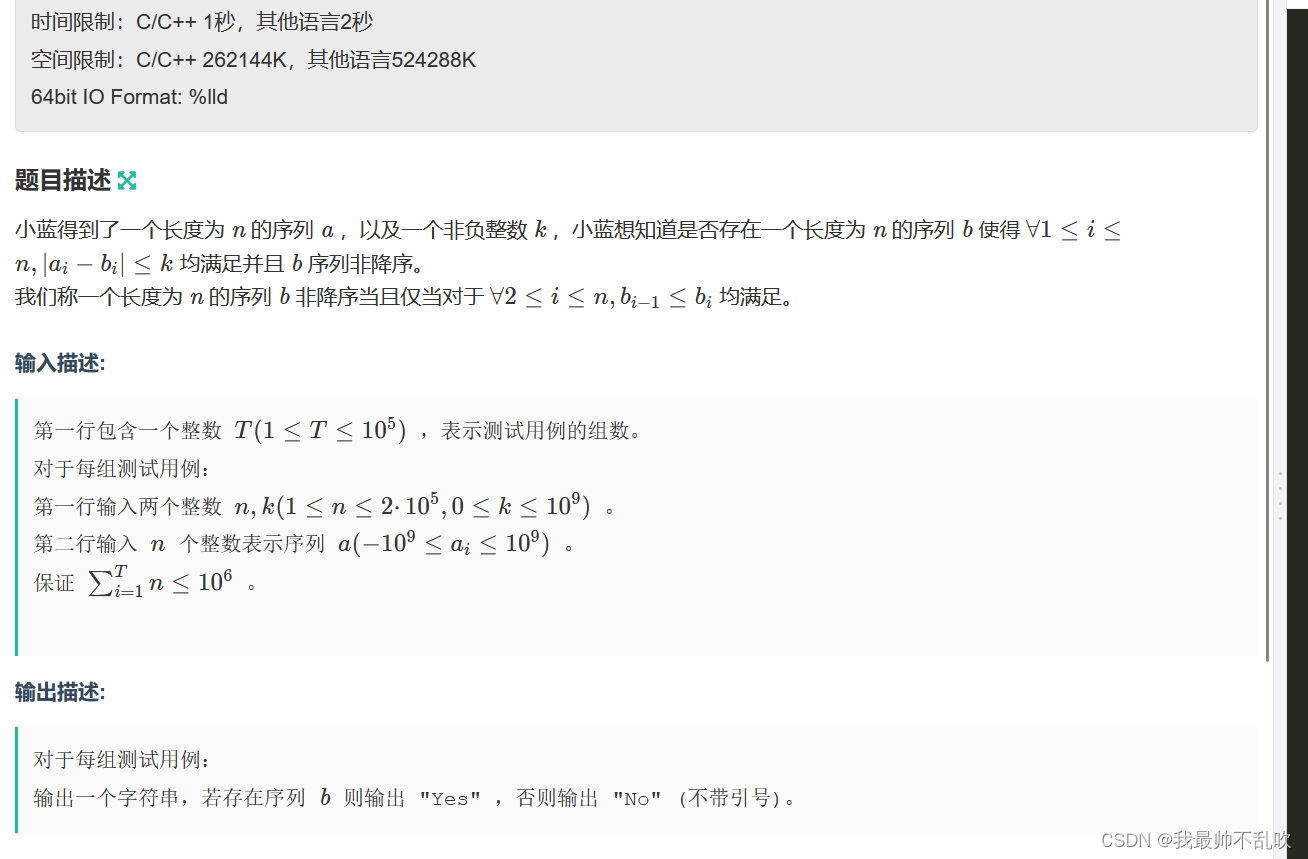
登录—专业IT笔试面试备考平台_牛客网
思路
明显看出,每输入一个数据然后我们处理一次,然后最后期望得到yes or no的结果。是很明显的贪心思路,(不太清楚的童鞋可以看该链接简单到爆炸der贪心算法学习及其证明方法其一:交换论证法-CSDN博客)
并且将分步的步骤(输入一个数据是一步)和最后想要的期望全局最优解(yes or no)的步骤都已经给定,则我们只需要思考如何对每一步进行处理即可。
则我们可以知道每一个数据都有一个值域,值域为该数字加k,减k。在这值域内取得数都满足与ai的差的绝对值<=k,符合作为序列b中元素,例如第一个数据输入2,则值域为(2-k,2+k)然后这个数的值域保留迭代与下一个数的值域比较,然后因为只用在意是否是非降序,即可也就是说考虑该值域下边界是否在下一个数的值域的上下边界内即可,所以只要设一个boundl作为迭代的下边界即可,不用考虑迭代的上边界的事。
如果下一个数的值域的上边界小于boundl,则不存在一个数字,在符合与ai的差值<=k的情况下并>=b(i-1)成为非降序序列。此时应返回No。
反之如果两值域有相交,则又应该分类讨论该数的下边界与boundl的大小:
如果下边界小于boundl,为了满足非降序序列,则可取的bi范围应舍弃boundl以下的范围,则boundl不变;
如果下边界大于boundl,为了满足差的绝对值<=k,则应该舍弃该值下边界下面的范围,将boundl迭代为该值的下边界;
最后判断是否出现过下一个数的值域的上边界小于boundl这种情况来决定是否输出No,反之输出Yes即可
参考代码实现
#include<bits/stdc++.h>
using namespace std;
using ll = long long;int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t; cin >> t;while (t--){int n, k, boundl, num, judge = 0;cin >> n >> k >> num; n--;boundl = num - k;while (n--){cin >> num;if (num + k < boundl)judge = 1;else{if (boundl<=num-k)boundl=num-k;}}if (judge)cout << "No" << endl;elsecout << "Yes" << endl;}
}end——





)




)


)




