数据结构（八）：图介绍及面试常考算法

一、图介绍

1、定义

图由结点的有穷集合V和边的集合E组成。其中，结点也称为顶点。一对结点（x， y）称为边（edge），表示顶点x连接到顶点y。边可以包含权重/成本，显示从顶点x到y所需的成本。若两个顶点之前存在一条边，就表示这两个顶点具有相邻关系。

2、类型

（1）无向图

（2）有向图

3、表示方法

（1）邻接矩阵

邻接矩阵存储结构就是用矩阵表示图中各顶点之间的邻接关系，两个顶点有邻接关系，就记录为1，否则为0。

（2）邻接表

邻接表是图的一种顺序存储与链式存储相结合的存储方式。

4、遍历方法

（1）广度优先搜索

（2）深度优先搜索

二、面试常考的算法

1、实现深度优先搜索

题目：如下无向图，从节点A开始遍历，其深度优先搜索为：A B D E F C。

思路：深度优先搜索，创建visited数组，用于记录所有被访问过的顶点。

（1）从A出发，访问A。

（2）找出A的第一个没有被访问的邻接点，访问该点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

（3）返回前一个访问过的仍有未被访问邻接点的顶点,继续访问该顶点的下一个未被访问邻接点。

（4）重复2,3步骤，直至所有顶点均被访问，搜索结束。

#include<iostream>
using namespace std;
#include<vector>
#include<set>
#include<unordered_set>
#include<map>class Graph{private:map<char, vector<char>> graph;  //创建图，graph记录图的节点及邻接关系public:void add_edge(char node, vector<char> neibors){graph[node] = neibors;}void dfs_helper(char node, map<char, int>& visited){visited[node] = 1;cout << node << " ";for(auto n: graph[node]){// 判断当前节点的邻接节点有无被访问if(visited[n] != 1)dfs_helper(n, visited);}}void dfs(char start_node){map<char,int> visited; // visited数组用来记录所有被访问过的顶点，被访问过，就记为1dfs_helper(start_node, visited);}  
};int main(){Graph graph;graph.add_edge('A', {'B', 'C'});graph.add_edge('B', {'A', 'D', 'E'});graph.add_edge('C', {'A', 'F'});graph.add_edge('D', {'B'});graph.add_edge('E', {'B', 'F'});graph.add_edge('F', {'C', 'E'});graph.dfs('A');
}

2、实现广度优先搜索

题目：如下无向图，从节点A开始遍历，其广度优先搜索为：A B D C E，从节点B开始遍历，其广度优先搜索为：B A C D E。

思路：广度优先搜索，利用队列来实现。把访问到的顶点入队，再访问该顶点的所有相邻的顶点，等访问完了该顶点的邻接点，再出队顶点和其相邻的顶点，每出队一个，就入队该顶点的未访问过的邻接顶点，重复上述步骤，直到队列为空。

#include<iostream>
#include<queue>
#include<map>
using namespace std;
class Graph{private:map<char, vector<char>> graph;  //创建图，graph记录图的节点及邻接关系public:void add_edge(char node, vector<char> neibors){graph[node] = neibors;}// 层次（广度）遍历void bfs(char node){map<char, int> visited; // visited数组用来记录所有被访问过的顶点，被访问过，就记为1queue<char> que;que.push(node);visited[node] = 1;while(!que.empty()){char temp = que.front(); //出队que.pop();cout << temp << " ";node = temp; //记录出队的点for(auto neibor: graph[node]){if(visited[neibor] != 1)que.push(neibor); //访问出队点的邻接点，并入队visited[neibor] = 1; //已访问的顶点标记为1}}}
};int main(){Graph graph;graph.add_edge('A', {'B', 'D'});graph.add_edge('B', {'A', 'C', 'D'});graph.add_edge('C', {'B', 'D', 'E'});graph.add_edge('D', {'A', 'B', 'C', 'E'});graph.add_edge('E', {'C', 'D'});graph.bfs('B');
}

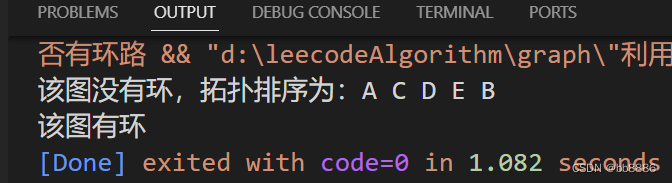
3、利用拓扑排序判断图是否有环路。

题目：如下有向图，判断是否存在环路。如果不为树，输出其拓扑排序。

思路：通过BFS实现拓扑排序。

（1）首先计算每个节点的入度，将所有入度为0的节点放入队列中

（2）开始执行BFS，我们取队首的节点u，放入结果中；移除u的所有出边，即将u的所有相邻节点的入度减少1，判断如果某个相邻的节点v的入度变为0，就将v放入队列中。

（3）当BFS结束后，如果答案中包含的节点数和图中的节点数相等，那么就得到了图G的拓扑排序，否则说明图中存在环，不存在拓扑排序。

// 利用拓扑排序判断有向图是否存在回路
#include<iostream>
#include<map>
#include<vector>
#include<queue>
using namespace std;
class Graph{private:map<char, vector<char>> graph;public:void add_edge(char node, vector<char> neibors){graph[node] = neibors;}// 广度优先搜索+队列判断void has_cycle(){map<char, int> indegree; //记录每个顶点的入度，默认为0for(auto g: graph){indegree[g.first] = 0;}//计算每个顶点的入度for(auto g: graph){char n = g.first;for(auto nei: graph[n]){indegree[nei] += 1;}}// 1、将所有入度为0的顶点入队queue<char> que;for(auto in: indegree){char c = in.first;if(in.second == 0)que.push(c);}// 2、开始执行BFS，每出队一个顶点，就将该顶点的所有边移除，// 即将该顶点所有相邻节点的入度减1，如果某个相邻节点的入度变为0，就将该节点放入队列中vector<char> tuopu;while(!que.empty()){char temp = que.front();que.pop();tuopu.push_back(temp);for(auto neibor: graph[temp]){indegree[neibor] -= 1;if(indegree[neibor] == 0)que.push(neibor);}}// 3.判断拓扑排序结果里的顶点个数，如果和图的个数相等，则没有环if(tuopu.size() == graph.size()){cout << "该图没有环，为树" << endl << "拓扑排序为：";for(auto t: tuopu){cout << t << " ";}    }elsecout << "该图有环，不为树";}
};int main(){// 没有环Graph graph;graph.add_edge('A', {'B', 'C'});graph.add_edge('B',{});graph.add_edge('C',{'D','E'});graph.add_edge('D', {'B'});graph.add_edge('E', {});graph.has_cycle();// 有环Graph graph2;graph2.add_edge('A', {'B', 'C'});graph2.add_edge('B', {'C'});graph2.add_edge('C',{'D','E'});graph2.add_edge('D', {'B'});graph2.add_edge('E', {});graph2.has_cycle();return 0;
}

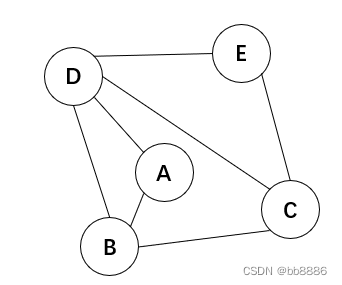
4、计算图的边数

题目：给定如下无向图，输出该图的边数7。

思路：遍历图中的节点，若该节点的邻接节点没有被访问，则边数count+1。

#include<iostream>
#include<queue>
#include<map>
using namespace std;
class Graph{private:map<char, vector<char>> graph;  //创建图，graph记录图的节点及邻接关系public:void add_edge(char node, vector<char> neibors){graph[node] = neibors;}// 计算图的边数void getNumsofEdge(){map<char, int> visited; //记录节点是否访问int count = 0;// 遍历graph中的节点与邻接节点for(auto g: graph){char n = g.first;for(auto neibor: graph[n]){if(visited[neibor] != 1){count += 1;}// 每遍历一个节点，就将该节点标记为1visited[n] = 1;}}cout << count;}
};
int main(){Graph graph;graph.add_edge('A', {'B', 'D'});graph.add_edge('B', {'A', 'C', 'D'});graph.add_edge('C', {'B', 'D', 'E'});graph.add_edge('D', {'A', 'B', 'C', 'E'});graph.add_edge('E', {'C', 'D'});graph.getNumsofEdge();
}

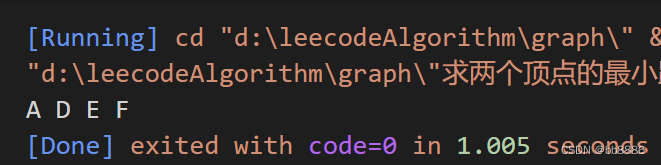
5、找到两个顶点之间的最短路径

题目：如下无向图，A到F的路径有A->B->C->E->F，A->B->C->F，A->D->E->F，输出最短路径A->D->E->F。

思路：广度优先搜索（BFS）+ 队列实现。

（1）准备queue和map，queue用于BFS，map<char, vector<char>>用于存储当前最短距离。

（2）BFS，将顶点node1入队，并向Map中添加键值对。

（3）当队列非空时，进行循环。现将队首元素x出队，当前路径等x的当前路径，然后遍历x的邻接节点，如果邻接点中的某个节点tmp不在map键值对中（相当于未访问过），就向Map中加入键值对<tmp，当前路径>，并将tmp入队，如果tmp为node2，就返回Map中tmp对应的路径。

#include<iostream>
#include<queue>
#include<map>
using namespace std;
class Graph{private:map<char, vector<char>> graph;  //创建图，graph记录图的节点及邻接关系public:void add_edge(char node, vector<char> neibors){graph[node] = neibors;}// 计算两个顶点的最短路径：A->B->D->Fvector<char> getShortPath(char node1, char node2){map<char, vector<char>> ShortPath;  //用于存储当前最短路径queue<char> q; //用于广度优先搜索// 如果求自身到自身的最短路径，返回node1->node2if(node1 == node2){return {node1, node2};}//否则将node1入队，并向map中加入键值对q.push(node1);ShortPath[node1] = {node1};while(!q.empty()){char temp = q.front();q.pop();vector<char> path = ShortPath[temp];for(auto neibor: graph[temp]){if(ShortPath.find(neibor) == ShortPath.end()){// 如果邻接节点不在map中（相当于未访问过），就向map中加入键值对ShortPath[neibor] = path;ShortPath[neibor].push_back(neibor);q.push(neibor);if(neibor == node2)return ShortPath[neibor];}}}return {};}
};
int main(){Graph graph;graph.add_edge('A', {'B', 'D'});graph.add_edge('B', {'A', 'C', 'D'});graph.add_edge('C', {'B', 'D', 'E'});graph.add_edge('D', {'A', 'B', 'C', 'E'});graph.add_edge('E', {'C', 'D', 'F'});graph.add_edge('F', {'C','E'});vector<char> short_path = graph.getShortPath('A', 'F');for(auto s: short_path){cout << s;}      
}