【hadoop】解决浏览器不能访问Hadoop的50070、8088等端口？！😎
- 前言🙌
- 【hadoop】解决浏览器不能访问Hadoop的50070、8088等端口？！
- 查看自己的配置文件：
- 最终成功访问如图所示：
- 总结撒花💞
😎博客昵称：博客小梦
😊最喜欢的座右铭：全神贯注的上吧！！！
😊作者简介：一名热爱C/C++，算法等技术、喜爱运动、热爱K歌、敢于追梦的小博主！
😘博主小留言：哈喽！😄各位CSDN的uu们，我是你的博客好友小梦，希望我的文章可以给您带来一定的帮助，话不多说，文章推上！欢迎大家在评论区唠嗑指正，觉得好的话别忘了一键三连哦！😘
前言🙌
哈喽各位友友们😊，我今天又学到了很多有趣的知识，现在迫不及待的想和大家分享一下！😘 都是精华内容，可不要错过哟！！！😍😍😍
【hadoop】解决浏览器不能访问Hadoop的50070、8088等端口？！
我不知道为什么网上查到的都是说解决浏览器不能访问Hadoop的50070、8088等端口？！然后我按照网上的说法就行访问，一直访问不了网页，最后觉着是不是根我们的配置文件数据有关，然后尝试了一下果然可以。其实我们的端口设计可能就不是通过这两个端口号来访问的。
访问解决办法：
1、首先确保自己能够在虚拟机命令行正常启动而且，jps指令等运行都可以。
2、保证将防火墙关闭
3、端口号访问要具体根据自己的配置文件来看，根据自己设置的端口号来进行访问Hadoop页面就可以了。
查看自己的配置文件：
- vim yarn-site.xml #查看yarn-site.xml文件
选红色这段的配置端口号进行访问即可 - vi hdfs-site.xml #查看hdfs-site.xml文件
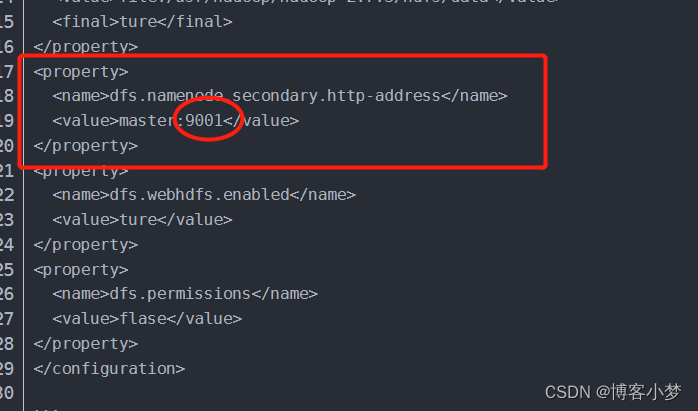
选红色这段的配置端口号进行访问即可
最终成功访问如图所示：
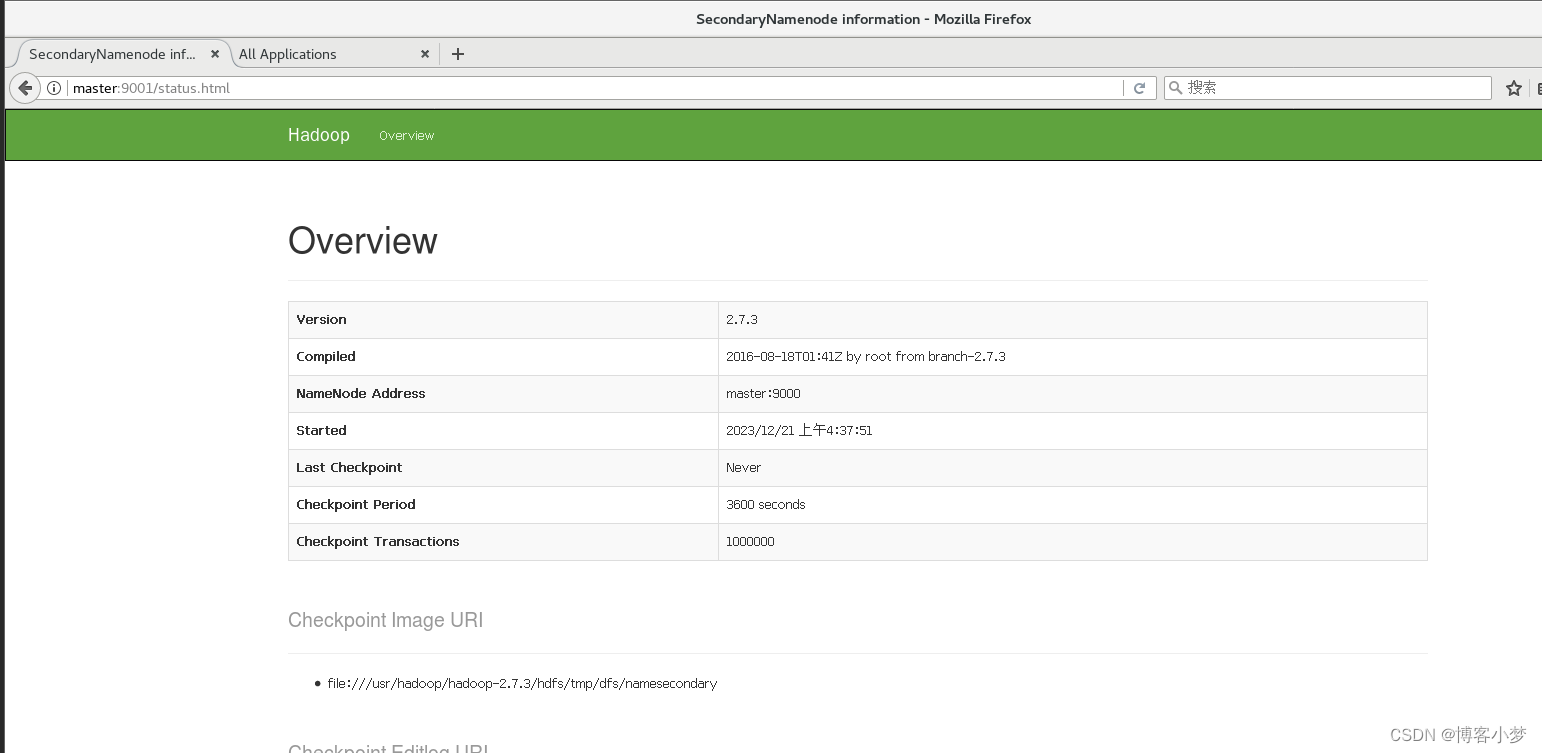
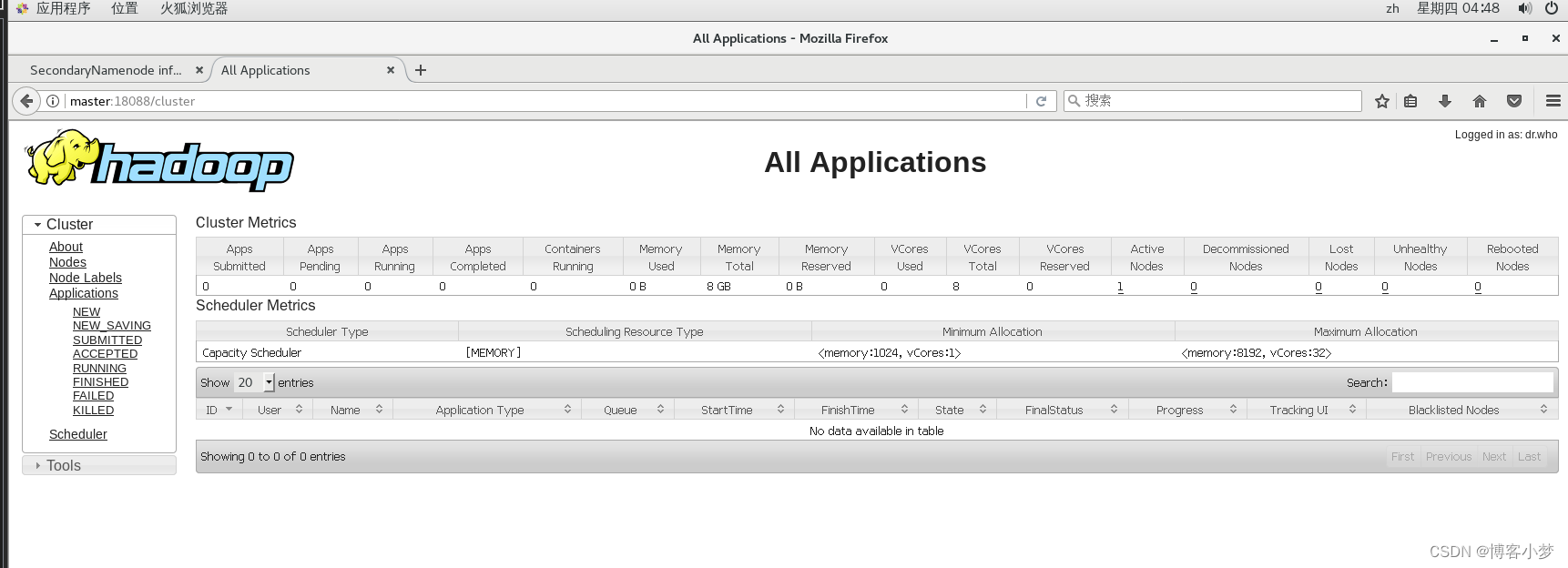
总结撒花💞
希望大家通过阅读此文有所收获！
😘如果我写的有什么不好之处，请在文章下方给出你宝贵的意见😊。如果觉得我写的好的话请点个赞赞和关注哦~😘😘😘
![[CVPR-23] Instant Volumetric Head Avatars](http://pic.xiahunao.cn/[CVPR-23] Instant Volumetric Head Avatars){kind=avatar}
