完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
1. dp数组的含义
dp[i][j] 0-i物品,重量为j的容量时,最大的价值
2. 递推公式
dp[i][j] = max(dp[i-1][j],dp[i][j-weight[i]]+value[i]);
两种状态,不用物品i的话,直接是用dp[i-1][j]
选用物品的话,为了重复使用物品i,其实是dp[i][j-weight[i]]+value[i],因为对dp[i][...]都是仍有机会再次使用物品i得
3.初始化dp[...][0]=0 由于重量为0,不可能有价值
dp[0][...] dp[0][j] = dp[0][j-wi]+vi;
4. 遍历顺序
物品和背包在外循环都可以(因为是二维),对背包空间需要是正向遍历,因为需要同行的前面的数据
压缩为1维dp:
把二维dp压缩为一行滚动更新//把dp[i-1]拷贝到dp[i]上
1. dp数组的含义
dp[j]重量为j的容量时,最大的价值
2. 递推公式
dp[j] = max([j],dp[j-weight[i]]+value[i]);
两种状态,不用物品i的话,直接是用dp[i-1][j]
3.初始化
dp[0]=0;(背包没有任何空间)
其他也初始化为0(非负的最小值),不会影响循环中的更新(需要用max,如果初始值太大,会影响递推公式)
4. 遍历顺序
根据递推公式:必须要正向遍历背包,因为在二维的角度看,会用到同一行,之前的数据
压缩来看:当前的数据更新 只需要dp[j-wi]+vi <--> dp[i][j-wi]+vi(由于正向遍历,在遍历到当前位置的时候,已经在一维dp数组中在当前位置的前方《0,j-1》全部更新了dp[i]层的数据,而当前j位置及以后仍然是dp[i-1]层数据),和dp[j] <->dp[i-1][j](其实就是上一层遍历储存在dp[i-1]层的数据)
而背包与物品的循环内外层关系并不重要了
对于01背包问题
如果倒序遍历背包,然后背包循环还在外面的话,dp[j-w]还在初始化状态时,就把dp[j]从0层到i层更新完了,(最终只会装入一个物品,当前容量下能装下的某一个物品且其价值最大)
所以必须先遍历物品,再对每个物品进行背包空间上的倒序遍历,这样在对第i层的dp[j]进行递推的时候,dp[j-wi]并不是初始化的值,而是已经计算过第i-1层的值了
对于完全背包问题
如果是正序的话,不论先遍历背包还是先遍历物品
在递推更新dp[j] 的时候需要的
dp[i] = max(dp[j],dp[j-weight[i]]+value[i]); dp[j]对应第i-1层 dp[j-wi]对应第N层(N 为物品个数),是提前算好的数据,但是由于是取最值,所以第N层的dp[j-wi]也是可以的,只要最后是整体的最大值就行了。与顺序无关。所以及时使用之后的数据也不影响最后的结果
举例:
| 重量 | 价值 | |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 60 |
| 物品2 | 4 | 30 |
先物品再背包
| 背包体积 | 0 | 1 | 2 | 3 | 4 |
| 物品0 | 0 | 15 | 30 | 45 | 60 |
| 物品1 | 0 | 15 | 30 | 60 | 75 |
| 物品2 | 0 | 15 | 30 | 60 | 75 |
先背包再物品
| 背包体积 | 0 | 1 | 2 | 3 | 4 |
| 物品0 | 0 | 15 | 30 | 45 | 75 |
| 物品1 | 0 | 15 | 30 | 60 | |
| 物品2 | 0 | 15 | 30 | 60 |
其实遍历下来跟二维dp还是有所不同因为在更新dp[j=4] (dp[i=0][j=4])的时候本来应该应用dp[i=0][j=3]+v1来跟0比较大小,但是先背包再物品的遍历顺序让当时的dp[j=3]其实是dp[i=2][j=3],所以dp[j=4]在i=0的时候已经是75了,但是并不影响,因为我们要取的是最大值,什么顺序,什么时候最大,并不影响最后结果,所以可以改变循环顺序
但是后面一题跟顺序有关,就不能随意改变循环顺序了
518.零钱兑换II
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
由于是求组合数,所以跟顺序没有关系
例如示例:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
1. dp 数组及含义
2维:dp[i][j] 的定义如下:
若只使用前 i 个物品(可以重复使用),当背包容量为 j 时,有 dp[i][j] 种组合方法可以装满背包
1维:dp[j]:凑成总金额j的货币组合数为dp[j]
2. 递推公式
2维
如果你不把这第 i 个物品装入背包,也就是说你不使用 coins[i-1] 这个面值的硬币,那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j],继承之前的结果。
如果你把这第 i 个物品装入了背包,也就是说你使用 coins[i-1] 这个面值的硬币,那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。
dp[i][j] = dp[i - 1][j] + dp[i][j-coins[i-1]];
1维:
dp[j] += dp[j - nums[i]];
3. 初始化
2维:base case 为 dp[0][..] = 0, dp[..][0] = 1。i = 0 代表不使用任何硬币面值,这种情况下显然无法凑出任何金额;j = 0 代表需要凑出的目标金额为 0,那么什么都不做就是唯一的一种凑法。
1维:dp[..][0] = 1由此可得之:
dp[j=0]=1; (目标为0的时候什么都不放就是一种方法)
由2维的 dp[0][..] = 0也可以看出,其他dp[j]初始化为0 对1维递推公式来说也是,初始化为0才不会影响累加公式的结果
4. 遍历顺序:
2维:背包正序遍历即可
两个循环内外部影响
1维:
先物品再背包,公式计算时是:dp[j]<-> dp[i][j]=dp[j]<->dp[i-1][j]+ dp[j - nums[i]]<->dp[i][j-nums[i]];
可以跟2维公式对应上
如果先循环背包再循环物品,从某点开始,dp[j-nums[i]]本应该对应2维的dp[i][j-nums[i]]却对应的是dp[N][j-nums[i]],因为递推公式是累加,之后的结果都会相应跟二维dp数组发生越来越大的结果
dp[j]<-> dp[i][j]=dp[j]<->无法对应+ dp[j - nums[i]]<->无法对应;
不同遍历方式一维dp数组打印:
例子:
- 输入: amount = 5, coins = [1, 2, 5]
先物品再背包
| 0 | 1 | 2 | 3 | 4 | 5 | |
| c1 | 1 | 1 | 1 | 1 | 1 | 1 |
| c2 | 1 | 1 | 2 | 2 | 3 | 3 |
| c5 | 1 | 1 | 2 | 2 | 3 | 4 |
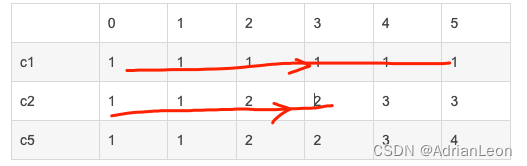
先背包再物品
| 0 | 1 | 2 | 3 | 4 | 5 | |
| c1 | 1 | 1 | 1 | 2 | 3 | 5 |
| c2 | 1 | 1 | 2 | 3 | 5 | 8 |
| c5 | 1 | 1 | 2 | 3 | 5 | 9 |
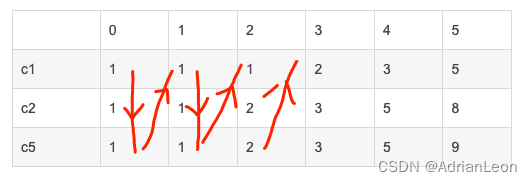
另一种理解方式:来源代码随想录

377. 组合总和 Ⅳ
其实本体本质不是一个完全背包问题,可以直接立即为:
每次能走1-n步的爬楼梯有多少种方法的问题
理解维爬楼梯问题后,可以简单直观的看出,我们必须先遍历到了第几层楼梯
再循环遍历这次爬几阶楼梯,这样每次dp[j]都讨论了会选择之前不同爬楼梯阶数的可能性dp[j]+=dp[j-nums[i]],所以其实把排列/顺序已经考虑在了其中
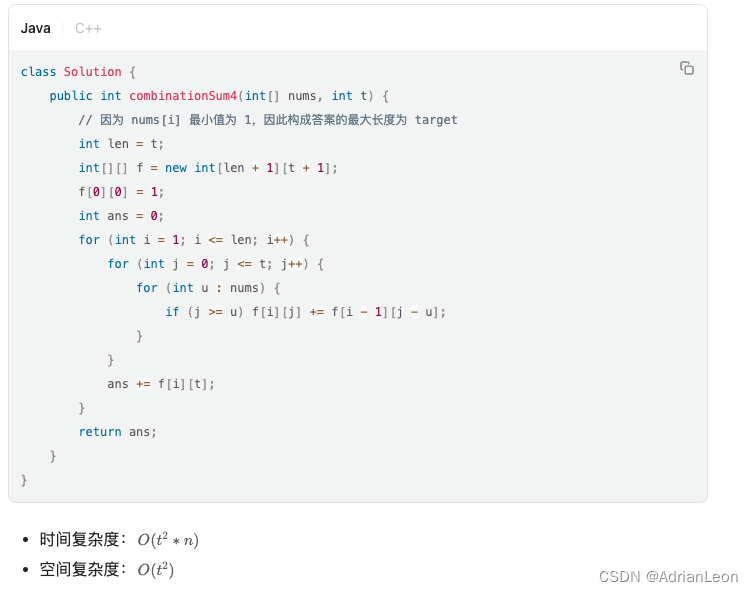
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target+1];dp[0]=1;for(int j=0;j<=target;j++){for(int i=0;i<nums.length;i++){if(j>=nums[i])dp[j]+=dp[j-nums[i]];}}return dp[target];}
}如果要用二维来理解:如下:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台


(二百二十八))





之容器和控件)







)



