球面谐波(SH)因为其良好的性质活跃在NeRF、Plenoxels、3DGS等显隐式场景表示的方法中。
问:球面谐波是什么?
答:一组基函数。可以理解为傅里叶分解的一种特殊形式,即“任何函数都可以用这组基的算术组合来近似”。
先描述一种通用情况:
假设我们有一组基数为3的完备基函数: [ e 1 ( x ) , e 2 ( x ) , e 3 ( x ) ] [e_1(x), e_2(x),e_3(x)] [e1(x),e2(x),e3(x)]
我们存在一个目标函数 f ( x ) f(x) f(x),那么 f ( x ) f(x) f(x)可以用这组基函数来表达:
f ( x ) = a 1 e 1 ( x ) + a 2 e 2 ( x ) + a 3 e 3 ( x ) f(x)=a_1e_1(x)+a_2e_2(x)+a_3e_3(x) f(x)=a1e1(x)+a2e2(x)+a3e3(x)这里的 [ a 1 , a 2 , a 3 ] [a_1,a_2,a_3] [a1,a2,a3]就是这组基的系数了。当然,我们可以用更“细致”的正交基来拟合目标函数,一般对应着更多的基数。我们可以浅看一张图:
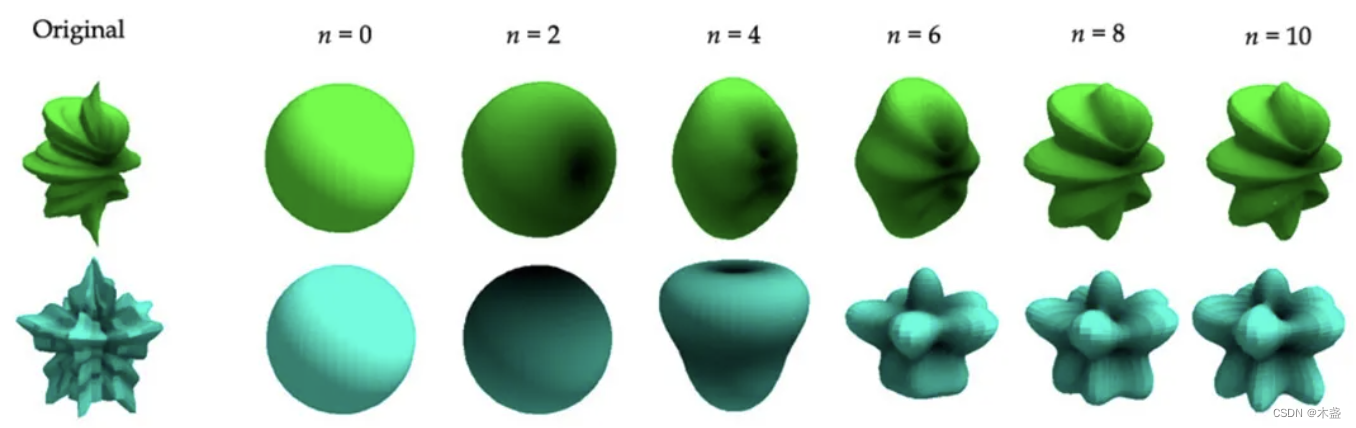
这里的n表示基数,用的是球面谐波基。由此可见,基数越多,拟合效果越佳。
球面谐波
球面谐波基,顾名思义,跟球面有关。首次将SH引入NeRF的工作是PlenOctrees。
未完待续…


)










 is undefined for the type JSONObject)

)



