第 N 个泰波那契数(easy)
题目链接:
1137. 第 N 个泰波那契数
题目描述:
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn+ + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
示例 1:
输入:n = 4 输出:4解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4示例 2:
输入:n = 25 输出:1389537
题目解析
注意,我们题目是泰波那契数,不是斐波那契数.
注意一下 Tn的定义,我们把n直接给赋值为0,此时变化为T3 = T0+ + T1 + T2 也即是 我们 给定一个数据 N, 那么TN等于前面三项之和.只要题目中给出我们前三项,那么此时我们就可以推导出第四,五…项.

算法原理
由于我们这里是第一个题目,我们先说一下我们之后要用到的名词.
什么是动态规划,一般而言,我们创建一个一维或者二维数组,我们把他们称之为
dp数组,后面我们想办法把这个表给填满,这个数组里面的某一个元素的值就是我们的答案.这个可以作为我们动态规划的流程.
状态表示: 对于数组里面的某一个位置的值可以理解为一个状态表示,他代表了一定含义.我们这里不说状态表示定义是什么,就说怎么得到这个值,毕竟这个名词实在是太严谨,我们先初步理解,有兴趣的朋友可以仔细的去查一下.
转台转移方程,如何得到一位置的确定值就是我们寻找状态转移方程的过程,一般而言,我们得到状态转移方程的思想有下面三个.
- 题目要求
- 题目要求+经验
- 分析问题过程中发现重复子问题
状态表示
这个很简单,我们可以把数组中的元素的值作为泰波那契数列的结果.
dp[i]: 表示 Ti的值
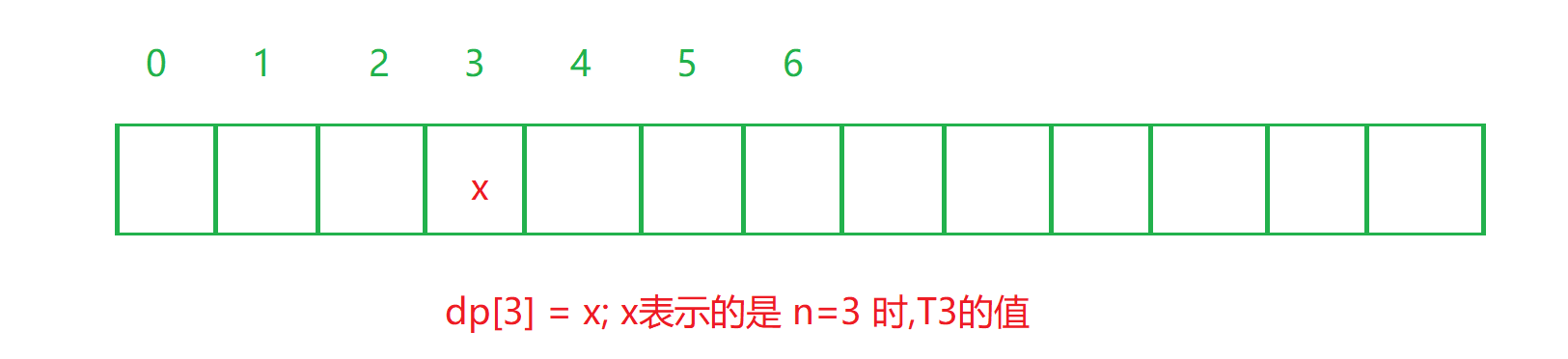
状态转移方程
这个很简单,题目上已经给了Ti = Ti-1+Ti-2+Ti-3
初始化
初始化的目的就是保证不越界,例如本题就是dp[i]要确定值,i必须从3开始出发,毕竟要找到前面三个元素的值,所以初始化为.
dp[0] = 0, dp[1] = 1,dp[2] = 1;
填表顺序
填表的顺序和我们逻辑顺序要一致,例如本题我们dp[i]是要看前面的元素,所谓我们这里从左向右.
返回值
这个看题目要求和我们的状态表示.题目要求我们返回第n个泰波那契数,我们dp[i]表示第n个泰波那契数,所以返回dp[n].
编写代码
class Solution {
public:int tribonacci(int n){if(n == 0)return 0;if(n == 1 || n == 2)return 1;// 我们要返回 dp[n]std::vector<int> dp(n+1);// 初始化dp[0] = 0;dp[1] = dp[2] = 1;// 方程for(int i = 3; i <= n; i++)dp[i] = dp[i-1]+dp[i-2]+dp[i-3];return dp[n];}
};

空间优化
由于我们是第一题,先把动态规划的完整流程给大家演示一下,后面我们就不谈空间优化的事情了.
对于动规的题目我们一般是使用滚动数组进行优化的,大家看一下这道题目.

我们可以发现我们求dp[i]的时候仅仅需要前面三个元素的值就可以了,像这些dp[i]仅仅需要前面若干的状态的情况我们可以使用滚动数组,例如我们可以定义一个容量为四个元素的数组,依次更新就可以了.
这里说一下优化的结果,一般空间复杂度可以降低一个数量级,例如O(N)的变化为O(1).
class Solution
{
public:int tribonacci(int n){if (n == 0)return 0;if (n == 1 || n == 2)return 1;int a = 0;int b = 1;int c = 1;int d = 0;for (int i = 3; i <= n; i++){d = a + b + c;a = b;b = c;c = d;}return d;}
};

三步问题(easy)
题目链接:
面试题 08.01. 三步问题
题目描述:
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3 输出:4说明: 有四种走法示例2:
输入:n = 5输出:13
题目解析
给定一定数量的台阶,例如10个.其中小孩子它可以一次跳1个台阶,2个台阶,3个台阶.问问我们我们总共有多少种方式可以到达第10个台阶.分析一下示例.
n = 3时, 我们可以这样跳.
方式1 : 1 1 1 每一次跳一个台阶
方式2 : 1 2 第一次跳一个, 第二次跳两个
方式3 : 2 1 第一次跳两个, 第二次跳一个
方式4 : 3 直接跳三个
算法原理
状态表示
这个需要我们的经验了,和数学相关的.我们让dp[i]表示到达第i个台阶我们的方法数.
状态转移方程
dp[i]表示到达第i个台阶的方法数,那么此时我们想如歌可以到达第i给台阶,这里很简单,有三个方式
i-1 下一步跳一个台阶
i-2 下一步跳两个台阶
i-3 下一步跳三个台阶
那么此时dp[i]分别就是这三个方式的和,也就是我们到达i-1和i-2以及i-3的方法数之和,正好dp[i]表示到达第i个台阶的方法数.
i-1 下一步跳一个台阶 dp[i-1]
i-2 下一步跳两个台阶 dp[i-2]
i-3 下一步跳三个台阶 dp[i-3]dp[i] = dp[i-1]+ dp[i-2]+ dp[i-3]
初始化
这里存在i-3,所以我们需要进行初始化.
dp[0] = 0, dp[1] = 1,dp[2] = 2; dp[3] = 4;
这里需要说一下,我们也是可以这样初始化的
dp[0] = 1, dp[1] = 1,dp[2] = 2;
这样初始化的意思主要是为了满足dp[3]的求值.
填表顺序
和前面一样从左先右.
返回值
题目要求给定一个n,求到达第n个台阶的方法数,这里就是dp[n]
编写代码
class Solution
{
public:int waysToStep(int n){if (n == 1)return 1;if (n == 2)return 2;std::vector<int> dp(n + 1);// 初始化dp[1] = 1;dp[2] = 2;dp[3] = 4;// 方程for (int i = 4; i <= n; i++)dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];return dp[n];}
};

这是因为题目中说了数据可能会溢出,所以这里我们两个数相加的时候需要处理一下.
class Solution
{
public:int waysToStep(int n){if (n == 1)return 1;if (n == 2)return 2;const int MOD = 1e9 + 7;std::vector<int> dp(n + 1);// 初始化dp[1] = 1;dp[2] = 2;dp[3] = 4;// 方程for (int i = 4; i <= n; i++)dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;return dp[n];}
};
使用最小花费爬楼梯(easy)
题目链接:
746. 使用最小花费爬楼梯
题目描述:
给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为
0或下标为1的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
题目解析
对于给定的数组,我们站在某一个确定的位置,然后花费该位置元素的代价后可以向后面移动一步或者两步,求我们到达楼梯顶部的花费.
此时我们需要知道的是我们的初始位置可以是从下标0或者1开始的.例如示例一数组为 [10,15,20],我们这里从下标1开始,直接跳两步就可以完成了.
在这道题中,数组内的每一个下标 [0, n - 1] 表示的都是楼层,而顶楼的位置其实是在 n 的位置!!!
算法原理
这里我们是题目要求+经验解题.我们用两个方法来解题.
解法一
状态表示
dp[i]表示以i位置为终点花费的最少的花费,注意:到达 i 位置的时候, i 位置的钱不需要算上
状态转移方程
可以到达i位置的有i-1和i-2位置,我们求他们花费的交小值,注意是我们计算较小值的时候是需要加上我们的代价的
dp[i] = min(dp[i-1]+const[i-1],dp[i-2]+const[i-2]).
初始化
这里的初始化有点意思,我们这里有i-2,所以我们这里初始化前两个.我们又可以知道我们初始的时候是可以选择0或者1的,那么0或者1位置的代价是0.所以我们这样做:dp[0] = 0,dp[1] = 0;
填表顺序
从左先右开始填.
返回值
我们要求的是到达n位置的最小花费,此时返回dp[n].
编写代码
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n+1, 0);for(int i = 2; i <= n; i++){dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);}return dp[n];}
};
解法二
状态表示
dp[i]表示以i位置为起点到达终点时需要花费的最少的花费.
状态转移方程
i位置为开始,此时我们可以跳到i+1或者i+2位置,如果i+1位置要跳到终点,按照我们的状态定义,此时应该是dp[i+1],同理i+2是dp[i+2].
我们知道,如果想要跳到i+1位置和i+2位置,我们在i位置是要花费代价的,此时这里的方程是.
dp[i] = min(dp[i+1], dp[i+2]) + const[i];
初始化
这里我们需要依赖i+1或者i+2的值,此时需要初始化dp[n],按照dp[i],我们从n位置到达n位置的花费是0.,这里我们需要注意的我们依赖i+2位置,这个时候我们需要从n-2位置开始填,那么问题来了,dp[n-1]填什么,这个很简单,他跳一步就可以到顶层,那么就是dp[i-1] = const[i-1]
填表顺序
这里是从右向左填.
返回值
按照状态定义,我们是从0位置或者1位置开始出发,到达顶部的最小花费,此时返回dp[0]和dp[1]的较小值.
编写代码
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n+1);dp[n] = 0;dp[n-1] = cost[n-1];for(int i = n-2; i >= 0; i--){dp[i] = min(dp[i+1], dp[i+2])+ cost[i];}return min(dp[0], dp[1]);}
};

解码方法(medium)
题目链接:
91. 解码方法
题目描述:
一条包含字母
A-Z的消息通过以下映射进行了 编码 :'A' -> "1" 'B' -> "2" ... 'Z' -> "26"要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,
"11106"可以映射为:
"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)注意,消息不能分组为
(1 11 06),因为"06"不能映射为"F",这是由于"6"和"06"在映射中并不等价。给你一个只含数字的 非空 字符串
s,请计算并返回 解码 方法的 总数 。题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12" 输出:2 解释:它可以解码为 "AB"(1 2)或者 "L"(12)。示例 2:
输入:s = "226" 输出:3 解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。示例 3:
输入:s = "06" 输出:0 解释:"06" 无法映射到 "F" ,因为存在前导零("6" 和 "06" 并不等价)。
题目解析
给定一个数字的字符串,我们是可以把它映射成一个只包含字母的字符串的,求我们可以映射多少种.映射的规则是1->a,2->b…26->z.注意一下,我们1可以映射为a,但是01确实不可以的.
算法原理
状态表示
题目要求+经验.
dp[i]: 以i位置为结尾,我们可以映射字符串的个数.
状态转移方程
这里分为两类.
i位置的字符单独作为一个映射, 如果可以映射,那么此时就是dp[i] = dp[i-1]. 注意我们求的是个数,这里是不能加1的.
i位置和前面一个字符进行映射,如果可以话,此时dp[i] = dp[i-2].
这两个情况都是可以的,所以我们的状态方程的结构是dp[i] = dp[i-1]+dp[i-2],具体的分析如下.
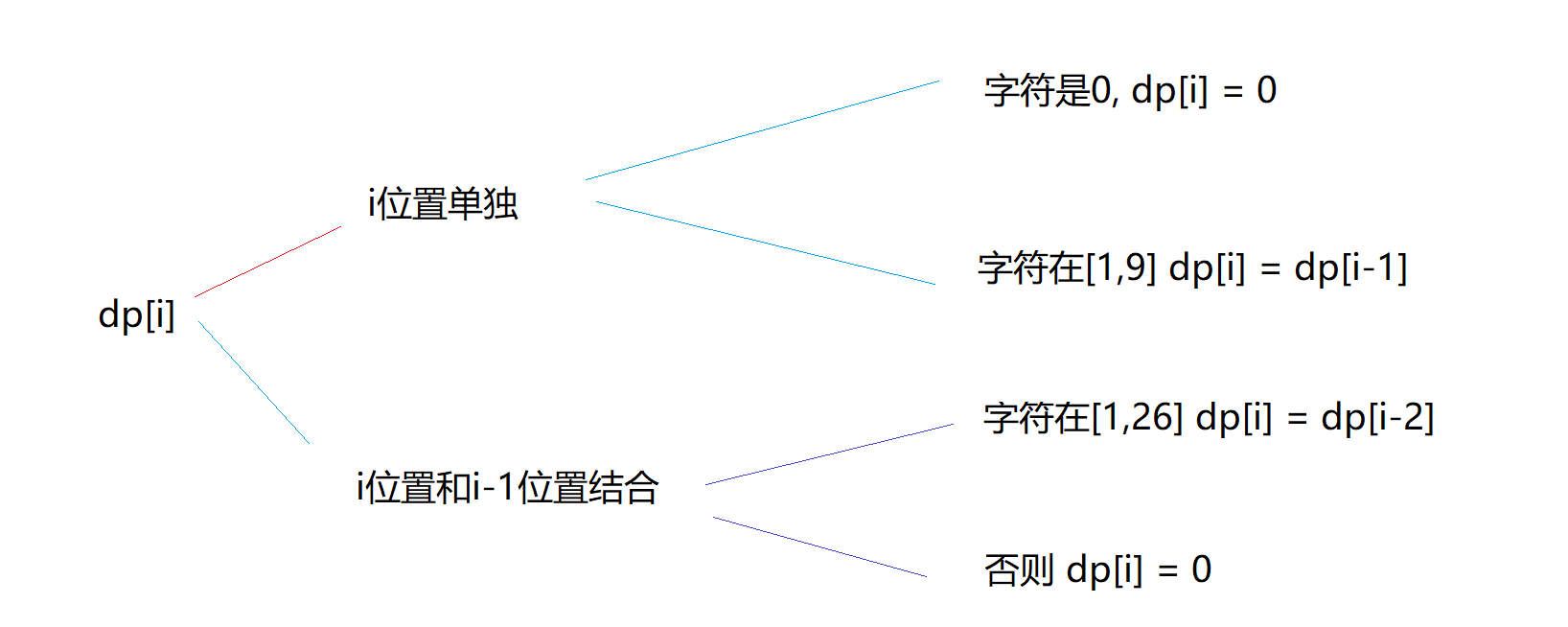
初始化
需要用到i-1和i-2,这里我们需要初始化dp[0]和dp[1],上面我们已经用过几次,这里我们换一个初始化方法.我们发现dp[0]比较好初始化,这里只需要关注dp[1],我们申请空间的时候额外申请多申请一个作为辅助节点,看下面.

对于str[1]位置而言,如果单独转化,此时只需要关注前面一个,也就是dp[1].如果和str[0]组合,此时需要知道的时如果可以组合成功,那么dp[2] = dp[0],那么dp[0]应该被初始化1.需要注意的,我们添加辅助节点之后,我们访问str的元素是需要下标适配的.
填表顺序
从左先右.
返回值
返回dp[n],之所以返回n位置的值,是因为我们添加了辅助节点.
编写代码
class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int> dp(n+1, 0);dp[0] = 1;for(int i = 1; i <= n; i++){// 单独一个 i-1 需要匹配if(s[i-1] != '0') dp[i] = dp[i-1];// 和前面一个字符匹配if(i-2>=0 && s[i-2]!='0' && (10*(s[i-2]-'0')+s[i-1]-'0') < 27)dp[i] += dp[i-2];}return dp[n];}
};








Vulnstack三层网络域渗透靶场)











