【数据结构】栈的使用|模拟实现|应用|栈与虚拟机栈和栈帧的区别

一、栈(Stack)

1.1 概念

1.2 栈的使用

1.3 栈的模拟实现

1.4 栈的应用场景

1. 改变元素的序列

2. 将递归转化为循环

3. 括号匹配

4. 逆波兰表达式求值

5. 出栈入栈次序匹配

6. 最小栈

1.5 概念区分

一、栈(Stack)

1.1 概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则（也就是先进后出）

压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶

出栈：栈的删除操作叫做出栈。出数据在栈顶

1.2 栈的使用

方法	功能
Stack()	构造一个空的栈
E push(E e)	将e入栈，并返回e
E pop()	将栈顶元素出栈并返回（有返回值）
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

public static void main(String[] args) {Stack<Integer> s = new Stack<>();s.push(1);s.push(2);s.push(3);s.push(4);System.out.println(s.size()); // 获取栈中有效元素个数---> 4System.out.println(s.peek()); // 获取栈顶元素---> 4s.pop(); // 4出栈，栈中剩余1 2 3，栈顶元素为3System.out.println(s.pop()); // 3出栈，栈中剩余1 2 栈顶元素为3if (s.empty()) {System.out.println("栈空");} else {System.out.println(s.size());}}

1.3 栈的模拟实现

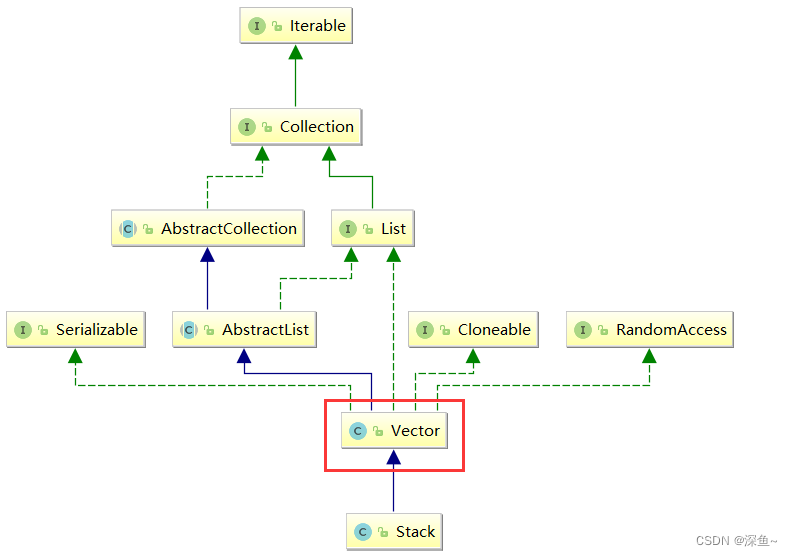
从上图中可以看到，Stack继承了Vector，Vector和ArrayList类似，都是动态的顺序表，不同的是Vector是线程安全的

栈的模拟实现有两种：一种是数组实现，另一种是链表（单链表或者双链表）实现，不管是哪种，都得保证入栈出栈操作的时间复杂度为O（1）

下面这个是数组模拟实现栈的方式：

import java.util.Arrays;//数组实现栈
public class MyStack {public int[] elem;//定义数组public int uesdSize;//记录当前数组的有效元素的个数，同时可以当作下标使用public static final int DEFAULT_CAPACITY = 10;//默认容量大小public MyStack() {this.elem = new int[DEFAULT_CAPACITY];}//判断栈是否满了public boolean isFull() {return uesdSize == elem.length;//这里不能写成DEFAULT_CAPACITY，DEFAULT_CAPACITY被final修饰不能变}//压栈 入栈public void push(int val) {if (isFull()) {this.elem = Arrays.copyOf(elem,2*elem.length);//扩容为原数组} else {elem[uesdSize++] = val;}}//判空public boolean isEmpty() {return uesdSize == 0;}//出栈public int pop() {if (isEmpty()) {throw new EmptyStackException("栈为空...");}int oldVal = elem[uesdSize-1];uesdSize--;elem[uesdSize] = 0;return oldVal;}//获取栈顶元素public int peek() {if (isEmpty()) {throw new EmptyStackException("栈为空...");}return elem[uesdSize-1];}
}

如果采用单向链表实现栈，那么为了保证入栈出栈的时间复杂度为O（1）

入栈只能采用头插法，尾插法需要遍历链表直到尾结点，这样就不满足时间复杂度为O（1）

出栈也只能采用头删法，可能大家会想用last来标记尾结点，从而不用遍历，但是这样在删除了一次以后，尾节点还得去遍历找前一个结点，还是不满足时间复杂度为O（1）

如果采用双向链表实现栈，那么头插尾插都是可以的

1.4 栈的应用场景

1. 改变元素的序列

1. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（）

A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1

2.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（）。

A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA

答：

1.由于栈的特性是先进后出，C选项中：当1，2，3都已经入栈后，3出栈，然后栈顶为2，不可能直接就让1进行出栈，所以错误

2.仍然考察的是栈的特性是先进后出，先进栈的元素最后出栈，那么也就是B

2. 将递归转化为循环

比如：逆序打印链表

// 递归方式void printList(Node head){if(null != head){printList(head.next);System.out.print(head.val + " ");}}

这里循环的方式就类似上面的第二题，入栈元素出栈也就相当于逆序

// 循环方式void printList(Node head){if(null == head){return;}Stack<Node> s = new Stack<>();// 将链表中的结点保存在栈中Node cur = head;while(null != cur){s.push(cur);cur = cur.next;}// 将栈中的元素出栈while(!s.empty()){System.out.print(s.pop().val + " ");}}

3. 括号匹配

首先思考一下为什么这个题需要用到栈这个数据结构，什么时候会用到这个数据结构？

一般和顺序有关的就需要考虑栈

这题的思路：

首先要明白这个题目不是偶数就一定是匹配的，eg：[（ ] ）

只要是左括号就入栈，遇到右括号就看是否匹配

以下三种情况是不匹配的：

（1）右括号不匹配就直接返回false

（2）字符串还没遍历完成但是栈是空的此时也是不匹配 eg：（））

（3）字符串遍历完了但是栈不为空此时也是不匹配 eg：（）（

class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();//遍历字符串for(int i=0;i<s.length();i++) {char ch = s.charAt(i);if(ch=='{'||ch=='['||ch == '(') {//左括号入栈stack.push(ch);} else {//右括号if(stack.isEmpty()) {//栈为空return false;} //栈不为空，右括号判断匹配char ch2 = stack.peek();if(ch2=='{'&&ch=='}'||ch2=='['&&ch==']'||ch2=='('&&ch==')') {stack.pop();} else {return false;}}}//遍历完了，但是栈不为空if(!stack.isEmpty()) return false;return true;//return stcak.isEmpty() 可以直接代替前三行}
}

注意：

（1) Stack<Character> stack = new Stack<>();这里的类型为Character

(2) ch2为左括号，ch为右括号

（3）怎么判断匹配，一组一组符合即可

4. 逆波兰表达式求值

看这题之前，我们先来学习一下什么是前中后缀表达式，中缀表达式转后缀表达式，最后再来看怎么根据后缀表达式计算结果

（1）中缀表达式：

操作符以中缀形式位于运算数中间（如：3+2），是我们日常通用的算术和逻辑公式表示方法

（2）后缀表达式：

又称逆波兰式（Reverse Polish Notation - RPN），操作符以后缀形式位于两个运算数后（如：3+2的后缀表达形式就是3 2 +）

（3）前缀表达式：

又称波兰式（Polish Notation），操作符以前缀形式位于两个运算数前（如：3+2的前缀表达形式就是+ 3 2）

手工如何将中缀表达式转后缀表达式？

以a+b*c+(d*e+f)*g为例，将其转为后缀表达式

（1）按先加减后乘除的原则给表达式加括号，得到的就是（ (a+(b*c) )+( ( (d*e)+f )*g ) ）

（2）由内到外把括号去掉，并把运算符放在要去掉括号的后面，也就是 abc*+ de*f+ g* +

计算器的逻辑就是这样的，会把我们输入的带有括号的表达式转为不带括号的表达式，因为计算器也不知道括号是啥

在这里代码题考的最多的就是根据后缀表达式计算结果，那么思路是什么呢？

将后缀表达式中的数字依次入栈，遇到运算数，就弹出栈顶的两个元素

第一个数字作为右操作数，第二个数作为左操作数，然后把 数字2 运算数数字1 计算得到的结果入栈（这个顺序不能改变）

然后继续这个过程，直到栈中只剩下最后一个元素，直接返回即可

代码实现：

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for(int i=0;i<tokens.length;i++) {String str = tokens[i];if(!isOperatons(str)) {//不是运算符，也就是数字//将字符串转为数字int val = Integer.valueOf(str);//将数字入栈stack.push(val);} else {//是运算符//弹除两个栈顶元素，第一个为右操作数int num2 = stack.pop();int num1 = stack.pop();//计算switch(str) {case "+":stack.push(num1+num2);break;case "-":stack.push(num1-num2);break; case "*":stack.push(num1*num2);break; case "/":stack.push(num1/num2);break;}}}return stack.pop();}//判断这个字符串是不是一个运算符private boolean isOperatons(String str) {if(str.equals("+")||str.equals("-")||str.equals("*")||str.equals("/")) {return true;} else {return false;}}
}

注意：

（1）入栈需要把字符串变为数字 int val = Integer.valueOf(str);

（2）弹除两个栈顶元素，第一个为右操作数，第二个为左操作数

5. 出栈入栈次序匹配

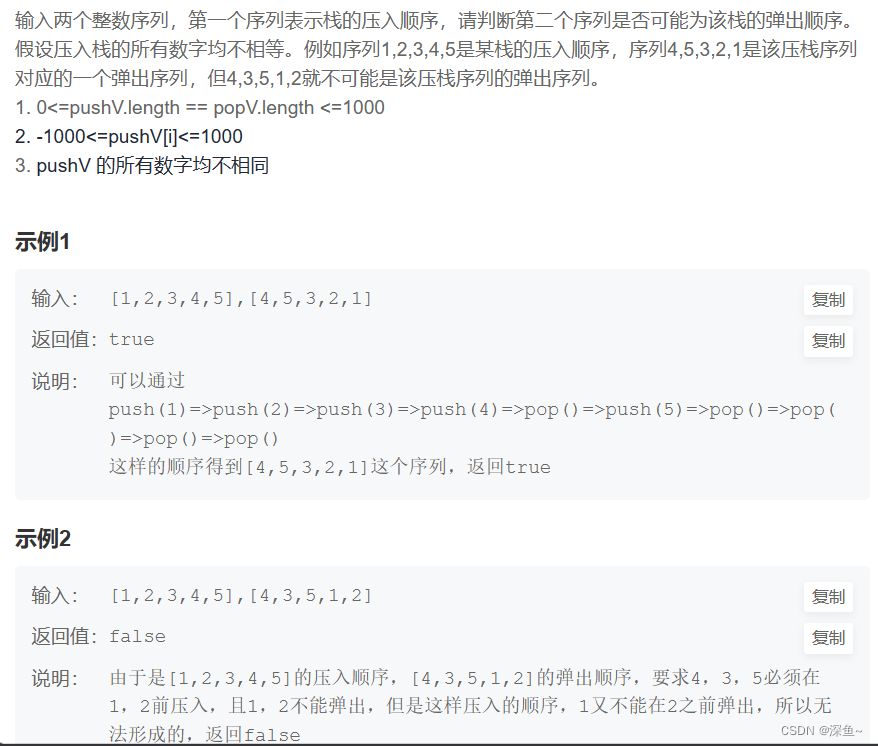
思路：

（1)遍历pushV数组，把pushV数组的元素放到栈当中

（2）每次放一个元素，就得看和popV的元素是否一样

（3）如果不一样，i++ 一样的话，j++，并将栈顶元素弹出（i是遍历pushA数组的，j是遍历popA数组的）

直到遍历完popV 结束

如下图当pushV栈顶元素和popV[j]一样，我们是需要将pushA的栈顶元素出栈的，不然无法判断下一个元素是否相等

public class Solution {public boolean IsPopOrder (int[] pushV, int[] popV) {Stack<Integer> stack = new Stack();int j =0;for(int i=0;i<pushV.length;i++) {stack.push(pushV[i]);//如果pushV栈顶元素和popV[j]一样while(!stack.isEmpty()&&j<popV.length&&stack.peek()==popV[j]) {j++;stack.pop();}}if(j<popV.length) {return false;}return true;//return j == popV.length;  //这里行可以代替前三行//return stack.isEmpty;   //或者这样写也行}
}

注意：当pushV栈顶元素和popV[j]一样时，可能存在 j下标越界，栈被弹空了的情况，所以需要特别考虑

6. 最小栈

思路：

这题一个栈无法得到最小元素的（如果最小元素不在栈顶，那么时间复杂度就不满足O（1），违背了题目条件），那么就考虑用两个栈

（1)普通栈Stack用来存储数据，最小栈minStack用来存最小元素

（2）普通栈一定要存有元素

（3）最小栈如果是第一次存放数据直接放，否则需要和最小栈的栈顶元素去比较 <=的时候才存入（这里特别注意一下=的时候，看图解释：这个时候如果右边的-3不放，当普通栈pop，最小栈也pop，那么最小值就不会是-3，而是-2，这显然不符合）

class MinStack {Stack<Integer> stack;Stack<Integer> minStack;//构造方法：初始化两个栈public MinStack() {stack = new Stack<>();minStack = new Stack<>();}public void push(int val) {stack.push(val);//如果第一次放（也就是minStack为空），直接放即可if(minStack.isEmpty()) {minStack.push(val);} else {//不是第一次放，那就只有val<= minStack栈顶元素才可以放if(val<= minStack.peek()) {minStack.push(val);}}}public void pop() {//根据题目不用考虑空栈int val = stack.pop();//如果普通栈pop出的元素就是最小，那么minStack也需要popif(minStack.peek()==val) {minStack.pop();}}//获取栈顶元素public int top() {return stack.peek();}//获取最小值public int getMin() {return minStack.peek();}
}