核心思路

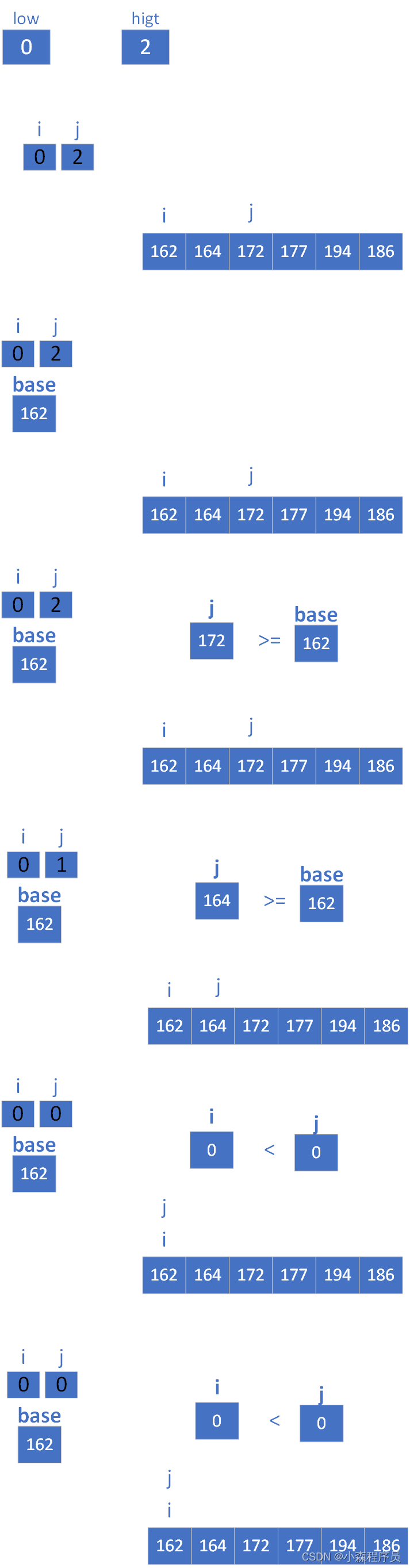
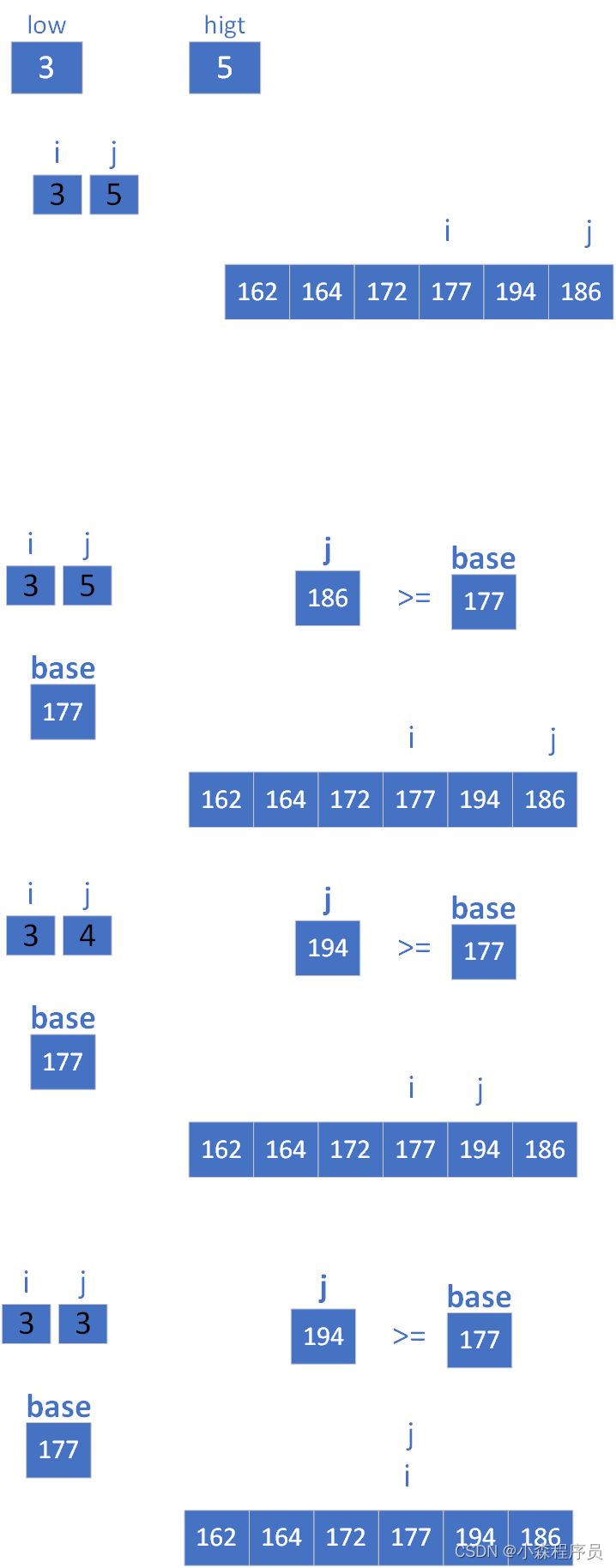
快速排序算法核心思路

选择一个“基准”元素，将数组分为两个子数组，一个包含比基准小的元素，另一个包含比基准大的元素，然后对这两个子数组进行递归排序。

基准数

初始化两个索引 i 和 j，分别子数组的开头和结尾。
初始化基准元素 base 为子数组的第一个元素。
如果子数组的长度大于1，执行以下步骤：
通过循环移动指针 j 从右向左，直到找到一个小于基准的元素或达到 i 的位置。
如果找到一个小于基准的元素，将其与 i 指向的元素交换，并将 i 向右移动一位。
通过循环移动指针 i 从左向右，直到找到一个大于基准的元素或达到 j 的位置。
如果找到一个大于基准的元素，将其与 j 指向的元素交换，并将 j 向左移动一位。
将基准元素放到 i 的位置。
返回 i 的值，表示基准元素在排序后的数组中的位置。

快速排序步骤

首先检查 low 是否小于 higt，如果不是，则说明子数组的长度小于等于1，不需要排序，直接返回。
调用 findbaseNum 函数找到基准元素的位置 baseIndex。
递归调用 QuickSort 函数对基准元素左边的子数组进行排序。
递归调用 QuickSort 函数对基准元素右边的子数组进行排序。

快速排序算法专区

// 定义一个函数FindBaseNum，它接受一个整数数组arr和两个整数Low和High作为参数。  
int FindBaseNum(int arr[], int Low, int High) {  // 初始化两个索引，i子数组的起始位置，j子数组的结束位置。  int i = Low;  int j = High;  // 选取子数组的第一个元素作为"基准"（pivot），也称为"轴"元素。  int base = arr[Low];  // 检查子数组的长度，如果子数组只有一个或没有元素，那么就没有排序的必要。  if (Low<High){  // 当i小于j时，循环继续。这个循环是快速排序的关键步骤，它不断地将数组划分为两部分，一部分是小于基准的元素，另一部分是大于基准的元素。  while (i<j) {  // 在j指针逐渐向内移动的过程中，检查其是否指向了一个小于或等于基准的元素。如果是，则继续移动。这个步骤确保了所有大于基准的元素都位于其左侧。  while (i<j&& arr[j]>=base) {  j--;  }  // 如果i小于j，将当前j指向的元素与i指向的元素交换。这一步操作确保了所有小于基准的元素都位于其右侧。同时，由于i指针已经移动到了一个位置，所以我们需要将其增加1以便在下一次迭代中检查正确的位置。  if (i<j) {  arr[i++] = arr[j];  }  // 确保了所有小于基准的元素都位于其右侧。同时，由于我们已经知道所有大于基准的元素都位于其左侧，所以我们可以简单地移动i指针来查找正确的位置。  while (i < j && arr[i] < base) {  i++;  }  // 如果i小于j，将当前i指向的元素与j指向的元素交换。这一步操作确保了基准位于其最终的位置上。同时，由于j指针已经移动到了一个位置，所以我们需要将其减少1以便在下一次迭代中检查正确的位置。  if (i < j) {  arr[j--] = arr[i];  }  }  // 将基准放在其最终的位置上。此时，我们只需要对基准左侧和右侧的两个子数组进行相同的操作即可完成排序。  arr[i] = base;  }  // 返回基准的位置索引。  return i;  
}// 定义一个函数QuickSort，它接受一个整数数组arr，以及两个整数low和higt作为参数。  
void QuickSort(int arr[], int low, int higt) {  // 如果low小于higt，则执行以下操作。这是递归的终止条件，意味着当low大于或等于higt时，数组已经被排序，不需要继续排序。  if (low<higt){  // 调用FindBaseNum函数来找到基准元素的索引。这个函数应该返回基准元素的位置。  int baseIndex = FindBaseNum(arr, low, higt);  // 对基准元素左边的子数组进行快速排序。  QuickSort(arr, low, baseIndex);  // 对基准元素右边的子数组进行快速排序。  QuickSort(arr, baseIndex + 1, higt);  }  
}

优化版，函数指针

// 函数 FindBaseNum 的定义。它接受一个整数数组 arr、两个整数 Low 和 High，  
// 以及一个函数指针 comp，该函数用于比较两个整数。  
int FindBaseNum(int arr[], int Low, int High,bool(*comp)(const int&,const int&)) {  // 初始化两个指针，i 指向子数组的起始位置，j 指向子数组的结束位置。  int i = Low;  int j = High;  // 选择子数组的第一个元素作为基准（pivot）。  int base = arr[Low];  // 如果子数组的长度大于1（至少有一个元素需要排序），则执行以下操作。  if (Low < High) {  // 当 i 小于 j 时，继续循环。这个循环是快速排序的关键步骤，它不断地将数组划分为两部分，  // 一部分是小于基准的元素，另一部分是大于基准的元素。  while (i < j) {  // 当 i 小于 j 且 arr[j] 大于或等于基准时，移动 j 指针到更小的位置。这确保了所有大于基准的元素都在其左侧。  while (i < j && !comp(arr[j],base)) {  j--;  }  // 如果 i 小于 j，交换 arr[i] 和 arr[j] 的值。这确保了所有小于基准的元素都在其右侧。  if (i < j) {  arr[i++] = arr[j];  }  // 当 i 小于 j 且 arr[i] 小于基准时，移动 i 指针到更小的位置。这确保了所有大于基准的元素都在其右侧。  while (i < j && comp(arr[i],base)) {  i++;  }  // 如果 i 小于 j，交换 arr[j] 和 arr[i] 的值。这确保了基准位于其最终的位置上。  if (i < j) {  arr[j--] = arr[i];  }  }  // 将基准放在其最终的位置上。此时，我们只需要对基准左侧和右侧的两个子数组进行相同的操作即可完成排序。  arr[i] = base;  }  // 返回基准的位置索引。  return i;  
}  // 函数 QuickSort 的定义。它接受一个整数数组 arr、两个整数 low 和 high，以及一个函数指针 comp，该函数用于比较两个整数。  
void QuickSort(int arr[], int low, int higt, bool(*comp)(const int&, const int&)) {  // 如果 low 小于 higt（子数组的长度大于1），则执行以下操作。  if (low < higt) {  // 找到基准的位置索引。  int baseIndex = FindBaseNum(arr, low, higt,comp);  // 对基准左侧的子数组进行快速排序。  QuickSort(arr, low, baseIndex,comp);  // 对基准右侧的子数组进行快速排序。  QuickSort(arr, baseIndex + 1, higt,comp);  }  
}  // 函数 QuickSort 的另一个定义，它接受一个整数数组 arr、数组的大小 size，以及一个函数指针 comp，该函数用于比较两个整数。  
void QuickSort(int arr[],int size, bool(*comp)(const int&, const int&)) {  // 如果 size 大于1且 comp 不为空（存在比较函数），则执行以下操作。这是递归的终止条件，意味着当 size 小于或等于1或 comp 为空时，数组已经被排序，不需要继续排序。  if (size>1&&comp) {  QuickSort(arr, 0, size-1, comp); // 从子数组的起始位置到结束位置进行排序。  }  
}