目录

一、选择题

二、编程题

三、选择题题解

四、编程题题解

---

一、选择题

1、请指出选择排序，冒泡排序，快速排序的时间复杂度分别是（）

A. O(n^2)、O(n^2)、O(n*log2n)

B. O(n*log2n)、、O(n^2)、O(n*log2n）

C. O(n)、O(n^2)、O(n^2)

D. O(n*log2n)、O(n^2)、O(n^2)

2、在单链表中，增加头结点的目的是（）

A. 标识表结点中首结点的位置

B. 算法实现上的方便

C. 使单链表至少有一个结点

D. 说明单链表是线性表的链式存储实现

3、下列算法的功能是什么？

/*L是无头节点单链表*/
LinkList Demo(LinkList L)
{ListNode *Q,*P;if(L&&L->next){Q=L;    L=L->next;P=L;while(P->next)P=P->next;p->next=Q;}return L;
}

A. 遍历链表

B. 链表深拷贝

C. 链表反转

D. 单链表转变为循环链表

4、表达式3*2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和运算符栈为(),其中^为乘幂

A. 3,2,4,1,1;(*^(+*-

B. 3,2,8;(*^-

C. 3,2,4,2,2;(*^(-

D. 3,2,8;*^(-

5、假设以数组A[60]存放循环队列的元素,其头指针是front=47,当前队列有50个元素,则队列的尾指针值为()

A. 3

B. 37

C. 97

D. 50

6、一棵完全二叉树第六层有9个叶结点（根为第一层），则结点个数最多有（）

A. 112

B. 111

C. 107

D. 109

7、有权值分别为11，8，6，2，5的叶子结点生成一棵哈夫曼树，它的带权路径长度为（）

A. 24

B. 71

C. 48

D. 53

8、已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，最后的叶子节点为（）

A. 34

B. 21

C. 16

D. 12

9、将10个元素散列到100000个单元的哈希表中,则()产生冲突

A. 一定会

B. 一定不会

C. 仍可能会

10、下列排序算法中，元素的移动次数与关键字的初始排列次序无关的是 （） 。

A. 直接插入排序

B. 起泡排序

C. 基数排序

D. 快速排序

二、编程题

1、年终奖    题目链接

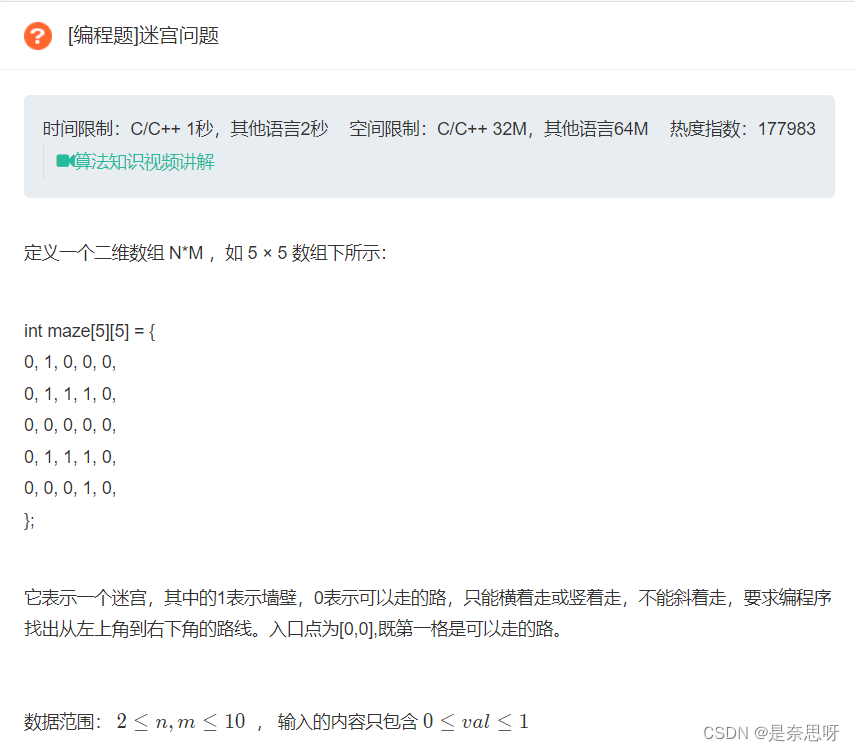
2、迷宫问题    题目链接

三、选择题题解

1、请指出选择排序，冒泡排序，快速排序的时间复杂度分别是（）

A. O(n^2)、O(n^2)、O(n*log2n)

B. O(n*log2n)、、O(n^2)、O(n*log2n）

C. O(n)、O(n^2)、O(n^2)

D. O(n*log2n)、O(n^2)、O(n^2)

正确答案：A

题解：

        基础题； 

2、在单链表中，增加头结点的目的是（）

A. 标识表结点中首结点的位置

B. 算法实现上的方便

C. 使单链表至少有一个结点

D. 说明单链表是线性表的链式存储实现

正确答案：B

题解：

        带头以后，在实现插入与删除等算法时会方便的多； 

3、下列算法的功能是什么？

/*L是无头节点单链表*/
LinkList Demo(LinkList L)
{ListNode *Q,*P;if(L&&L->next){Q=L;    L=L->next;P=L;while(P->next)P=P->next;p->next=Q;}return L;
}

A. 遍历链表

B. 链表深拷贝

C. 链表反转

D. 单链表转变为循环链表

正确答案：D

题解：

        我们发现Q存的是第一个结点的位置，while循环是找最后一个结点，并存入P中，最后将P的next指向Q完成首尾相连；

4、表达式3*2^(4+2*2-6*3)-5求值过程中当扫描到6时,对象栈和运算符栈为(),其中^为乘幂

A. 3,2,4,1,1;(*^(+*-

B. 3,2,8;(*^-

C. 3,2,4,2,2;(*^(-

D. 3,2,8;*^(-

正确答案：D

题解：

         此题考察利用栈将中缀表达式转后缀表达式，具体规则是分别使用两个栈，一个为数据栈，一个为运算符栈，遍历中缀表达式，遇到数字则将数字入数据栈，遇到运算符有三种情况，若运算符栈为空，则入栈；若运算符栈不为空且当前运算符大于栈顶运算符，则直接入栈，若运算符栈不为空且当前运算符小于等于运算符栈顶符号，则取出数据栈顶两个数据用运算符栈顶的运算符进行计算，然后将结果继续入栈；

5、假设以数组A[60]存放循环队列的元素,其头指针是front=47,当前队列有50个元素,则队列的尾指针值为()

A. 3

B. 37

C. 97

D. 50

正确答案：B

题解：

         （47 + 50） % 60 = 37；

6、一棵完全二叉树第六层有9个叶结点（根为第一层），则结点个数最多有（）

A. 112

B. 111

C. 107

D. 109

正确答案：D

题解：

         首先我们要清楚二叉树的两个特性，第 n 层的结点个数2^(n - 1)，满二叉树 n 层结点的总数为2^n - 1；我们首先算出第6层结点个数2^(6 - 1) = 32；而第六层只有9个结点，因此必然存在第七层；我们算出7层总共结点数位2^7 - 1 = 128；然后减去9 * 2；就是完全二叉树的最多节点个数；

7、有权值分别为11，8，6，2，5的叶子结点生成一棵哈夫曼树，它的带权路径长度为（）

A. 24

B. 71

C. 48

D. 53

正确答案：B

题解：

         我们首先要会画出我们的哈夫曼树，画出如下图所示；

 

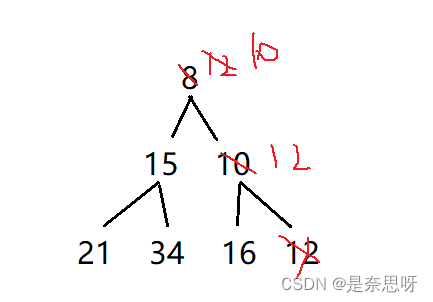
8、已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，最后的叶子节点为（）

A. 34

B. 21

C. 16

D. 12

正确答案：C

题解：

         具体过程如下图所示；

 

9、将10个元素散列到100000个单元的哈希表中,则()产生冲突

A. 一定会

B. 一定不会

C. 仍可能会

正确答案：C

题解：

         哈希函数只能尽量减少冲突，无法避免冲突；

10、下列排序算法中，元素的移动次数与关键字的初始排列次序无关的是 （） 。

A. 直接插入排序

B. 起泡排序

C. 基数排序

D. 快速排序

正确答案：C

题解：

         基数排序元素移动次数与其实次序无关，只与即最大数据的权重位数有关；

四、编程题题解

1、年终奖

思路：采用动态规划的思路，我们定义dp[i][j]为以 i 行 j 列结尾的位置最大价值；不难推出该最大价值为dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + 当前格子价值；

class Bonus 
{
public:int getMost(vector<vector<int> > board) {int m = board.size();int n = board[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));for(int i = 1; i <= m; i++)for(int j = 1; j <= n; j++)dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + board[i - 1][j - 1];return dp[m][n];}
};

2、迷宫问题

思路：经典的一道DFS题目，我们标记每个位置是否走过，到终点时记录并更新最短路径；

#include <iostream>
#include <type_traits>
#include <vector>
using namespace std;vector<vector<int>> maze, curpath, bestpath;
vector<vector<bool>> is_arrive;
int row, col;void get_road(int x, int y)
{is_arrive[x][y] = true;curpath.push_back({x, y});// 到达终点if(x == row - 1 && y == col - 1){if(bestpath.empty())bestpath = curpath;elseif(curpath.size() < bestpath.size())bestpath = curpath;}// 开始移动探测 右、下、左、上if(y + 1 < col && is_arrive[x][y + 1] == false && maze[x][y + 1] == 0)get_road(x, y + 1);if(x + 1 < row && is_arrive[x + 1][y] == false && maze[x  + 1][y] == 0)get_road(x + 1, y);if(y - 1 >= 0 && is_arrive[x][y - 1] == false && maze[x][y - 1] == 0)get_road(x, y - 1);if(x - 1 >= 0 && is_arrive[x - 1][y] == false && maze[x - 1][y] == 0)get_road(x - 1, y);// 回溯is_arrive[x][y] = false;curpath.pop_back();
}int main()
{cin >> row >> col;// 初始化maze.resize(row, vector<int>(col, 0));is_arrive.resize(row, vector<bool>(col, false));for(int i = 0; i < row; i++)for(int j = 0; j < col; j++)cin >> maze[i][j];get_road(0, 0);for(int i = 0; i < bestpath.size(); i++)cout << "(" << bestpath[i][0] << "," << bestpath[i][1] << ")" << endl;return 0;
}