数据结构：树（Tree）

树型结构

树的概念

树是一种非线性结构，他是由n（n>=0）个有限结点组成的一个具有层次关系的集合。当n=0时，该树为空树。在任意一个非空树中都满足以下条件：
1、有一个特殊的结点，称为根结点，根结点没有前驱结点
2、当n>1时，其他结点可分为M（M>0）个互不相交的有限集T1，T2，T3.……、Tm，其中每个集合本身又是一棵与树类似的子树，每个子树的根结点有且只有一个前驱结点，后继结点可以有n个或多个。
3、树是递归定义的，树离不开递归。
4、在n个结点的树中有n-1条边。

树的一些基本特点和术语

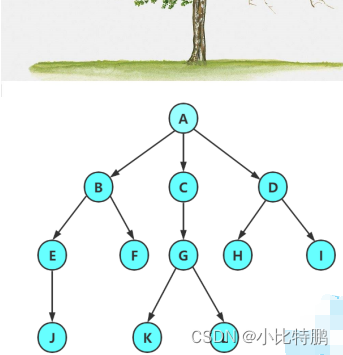
在这里插入图片描述
如图树型结构中，子树之间不能有交集否则就不是树型结构
通过上面那张图可以看出树的一些基本概念

结点的度：一个结点含有子树的个数称为该节点的度；通过上图：A结点的度为3.
树的度：一棵树中，所有结点度的最大值称为树的度；如上图：树的度为3.
叶子结点或终端结点：度为0的结点称为叶子结点；如上图：J、F、K、L、H、I结点是叶子结点。
双亲结点或父结点：若一个结点含有子节点，则这个结点称为其子节点的父结点；如上图：A是B、C、D的双亲结点。
孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点；如上图：B、C、D结点是A结点的子节点。
根结点：一棵树中没有双亲结点的结点；如上图：A结点是树的根结点。
结点的层次：从根开始定义起，根为第一层，根的子节点为第二层，以此类推下去。
树的高度：树中结点的最大层次；如上图：树的高度为 4 。
以上就是树的一些重要的概念下面还有一些需要我们去了解一下的概念。
非终端结点或分支结点：度不为0的结点；如上图：B、C、D等结点为分支结点。
兄弟结点：具有相同父节点的结点称为兄弟结点；如上图：B、C、D是兄弟结点；
堂兄弟结点：双亲在同一层的结点互为堂兄弟；
森林：由m（m>=0）棵互不相交的树组成的集合称为森林。
还有就是结点的深度和高度的区别：
结点的深度是从根结点开始自顶向下逐层累加的。
结点的高度则是从叶子结点开始自底向上逐层累加的。
最后一点树也分为有序树和无序树
如果该树的各个结点都是从左到右是有次序的，不能互换；则称为有序树，否则是无序树。如果是有序树，若将子结点位置互换，则会变成一棵不同的树。

至此兄弟们应该了解树的一些基本结构和专业名词了吧！且一定要记住树是非线性的且树离不开递归。
接下来我们开始树的相关性质的学习

树的性质

1、度为m的树中第i层上至多有m的（i-1）次方个结点
2、树中的结点数等于所有结点的度数加1

树的表示形式

树有很多表示方式：孩子双亲表示法，双亲表示法，孩子表示法，孩子兄弟表示法等
我们可以简单了解一下最常用的一种表示方法：孩子兄弟表示法
任何一棵树，他的结点的第一个孩子都是唯一的，他的右兄弟如果存在也是唯一的
所以有这种结点结构：
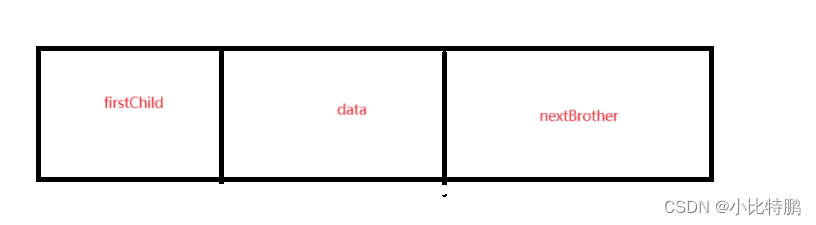
在这里插入图片描述

public class Tree {int value;  //存储的数据Tree firstChild;  //第一个孩子Tree nextBrother;//下一个兄弟
}

这就让我们想到二叉树一种神奇的树

再此之后还有一种树值得我们去深入探究——那便是二叉树

二叉树

二叉树的定义

二叉树也是一种树型结构，他的每个结点至多有2个子树（二叉树中不能存在度大于2的结点），其子树有左右之分不能调换这是有序树。

二叉树和树相似都离不开递归。
空树也是二叉树
以下就是二叉树的5种基本形态如图所示：
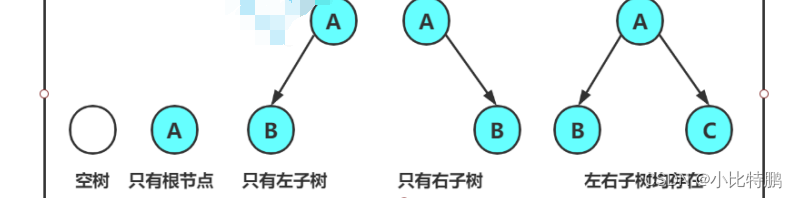
在这里插入图片描述

特殊的二叉树

1、满二叉树：一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。如下图：
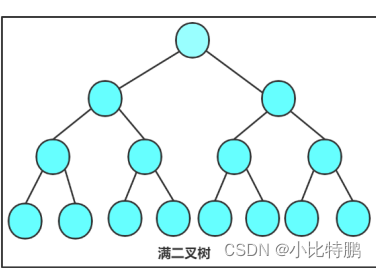
在这里插入图片描述
2、完全二叉树：完全二叉树是一种效率很高的数据结构。一个高度为h，n个结点的二叉树，当且仅当其每个结点都与高度为h的满二叉树中编号从0~n-1的结点一一对应则称为完全二叉树。相信火眼精金的朋友们也发现了满二叉树是一种特殊的完全二叉树。
完全二叉树如图所示：
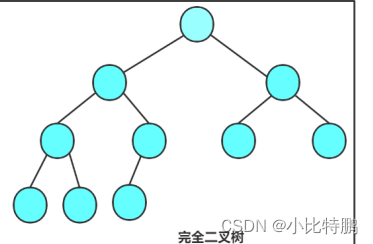
在这里插入图片描述
重点：完全二叉树度为1 的结点个数只能是1或者0。
3、二叉排序树
二叉排序树的定义为：左子树上的所有结点的关键字均小于根节点的关键字；右子树的所有结点的关键字均大于根结点的关键字。左子树和右子树也是一棵二叉排序树。
4、平衡二叉树
任意结点的左子树和右子树的深度之差不能超过1.

二叉树的性质

1、若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)(i>0)个结点。
2、若规定只有根节点的二叉树的深度为1，则深度为K的二叉树最大结点数为：2^K -1（K>=0）
3、对于任意一棵二叉树，如果其叶子结点个数为n0，度为2的非叶子结点个数为n2，则n0 = n2 +1
4、具有n个结点的完全二叉树的深度K为log2（n+1）上取整
5、具有n个（n>0）结点的完全二叉树的高度为【log2 n】+1
6、对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有结点从0开始编号，则对于编号为i的结点有：
. 若i>0，双亲的编号：（i-1)/2; i=0, i为根节点编号，无双亲结点。
. 若2i +1<n,左孩子编号：2i+1，否则没有左孩子
. 若21+2<n，右孩子编号：2i+2，否则没有右孩子

树的遍历

树的遍历分为三种分别是前序遍历、中序遍历、后序遍历。
前序遍历的顺序是：根->左子树->右子树.
中序遍历的顺序是：左子树->根->右子树.
后序遍历的顺序是：左子树->右子树->根.

代码实现如下：

public class BinaryTree {static class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val) {this.val = val;}}public TreeNode createTree(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;return A;}//前序遍历public void preOrder(TreeNode root){if (root == null){return;//空树}System.out.println(root.val+" ");preOrder(root.left);preOrder(root.right);}//中序遍历public void inOrder(TreeNode root){if (root == null){return;}inOrder(root.left);System.out.println(root.val+" ");inOrder(root.right);}//后序遍历public void postOrder(TreeNode root){if (root == null){postOrder(root.left);postOrder(root.right);System.out.println(root.val+" ");}}
}

下面是我觉得比较有意思的题：
在这里插入图片描述
就比如上面这道相信同学们第一眼看到求叶子结点就想到了我们二叉树的一个重要性质：n0=n2+1；且n=n0+n1+n2 但是仅仅靠这两个条件和题中所给的信息还是算不出来通过画图我们可以知道完全二叉树度为1的结点只有两种情况那就是n1不是0个就是1个
加上这个完全二叉树的性质解决这道题就轻而易举了
大家可以去试试哈