接雨水

引言

编写通过所有测试案例的代码并不简单，通常需要深思熟虑和理性分析。虽然这些代码能够通过所有的测试案例，但如果不了解代码背后的思考过程，那么这些代码可能并不容易被理解和接受。我编写刷题笔记的初衷，是希望能够与读者们分享一个完整的代码是如何在逐步的理性思考下形成的。我非常欢迎读者的批评和指正，因为我知道我的观点可能并不完全正确，您的反馈将帮助我不断进步。如果我的笔记能给您带来哪怕是一点点的启示，我也会感到非常荣幸。同时，我也希望我的分享能够激发您的灵感和思考，让我们一起在编程的道路上不断前行~

接雨水

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

图片来源

提示

• n == height.length
• 1 <= n <= 2 * 10⁴
• 0 <= height[i] <= 10⁵

解决方案1：【动态规划】

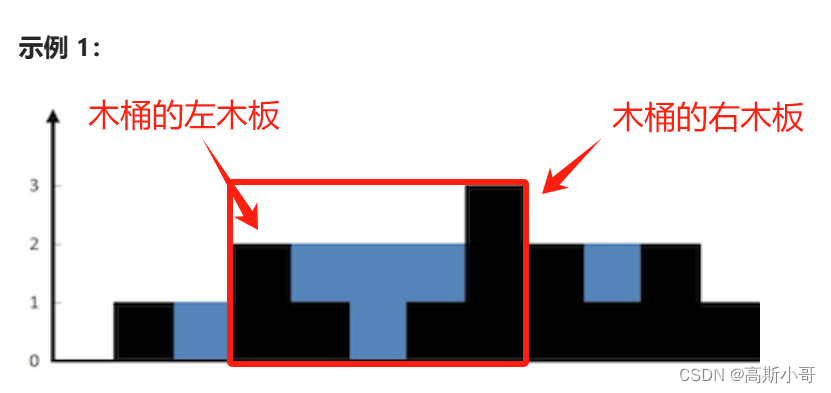
通过观察图像，我们可以发现红色方框部分与木桶的形态颇为相似。让我们富有想象力地将最左侧高度为2的柱子视作木桶的左侧板，而将最右侧高度为3的柱子视作木桶的右侧板。基于深入人心的【木桶原理】，一个木桶的装水量总是受限于其最短的那块木板。这就意味着，木桶内的水柱高度+柱子高度与左侧板的高度相等时，即达到装水的极限。

更为精妙的是，对于图中的每个位置i，我们都可以将其左侧最高的柱子想象为木桶的左侧板，而将右侧最高的柱子视为木桶的右侧板。这样一来，每个位置的水柱高度+柱子高度height[i]之和，便取决于左侧板和右侧板中较低的那个，恰如木桶原理中所蕴含的深邃智慧。

问题1：对于每个位置i，如何获取其左侧最高柱子的高度left_max[i]和右侧最高柱子的高度right_max[i]呢？

可以通过两次遍历数组height进行获取，代码如下：

# 木桶理论
# 对于位置i，left_max[i]记录的是其左侧最高柱子的高度
left_max = [0] # 对于第0根柱子，其左侧没有柱子，默认其左侧最高柱子的高度为0
# 对于位置n-1-i，right_max[i]记录的是其右侧最高柱子的高度
right_max = [0] # 对于最后一根柱子，其右侧没有柱子，默认其右侧最高柱子的高度为0n = len(height)
# 顺序遍历
for i in range(1, n):# 对于位置i，left_max[-1]记录的是位置i-1其左侧最高柱子的高度---> 只需要和位置i-1的高度height[i-1]进行比较并取最大值即可得到位置i其左侧最高柱子的高度left_max.append(max(left_max[-1], height[i-1]))
# 逆序遍历
for i in range(n-2, -1, -1):# 对于位置i，right_max[-1]记录的是位置i+1其右侧最高柱子的高度---> 只需要和位置i+1的高度height[i+1]进行比较并取最大值即可得到位置i其右侧最高柱子的高度right_max.append(max(right_max[-1], height[i+1]))
# 因为是逆序遍历，需要将结果反转 ---> 反转后, right_max[i]记录的是位置i其右侧最高柱子的高度
right_max = right_max[::-1]# 验证结果
for i in range(n):print("对于第{}根柱子，其高度为{}, 其左侧最高的柱子高度是{},其右侧最高的柱子高度是{}".format(i, height[i], left_max[i], right_max[i]))

运行结果：

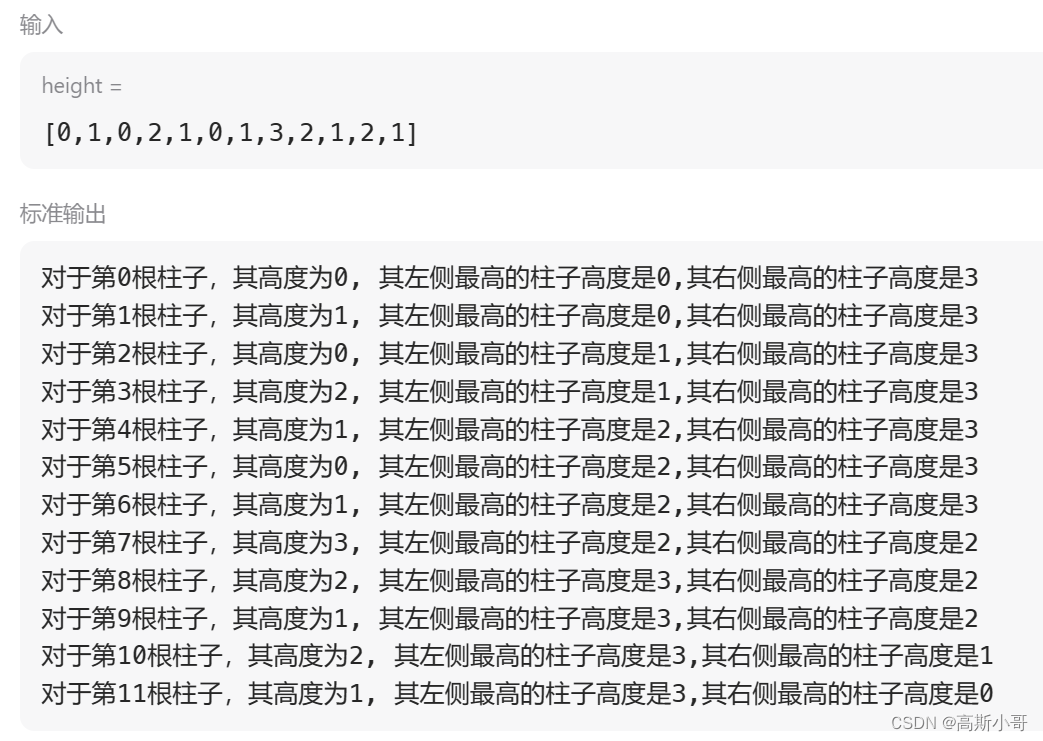
观察上图的输入height以及标准输出，可以发现算法成功获取到每个位置i的左侧最高柱子的高度left_max[i]和右侧最高柱子的高度right_max[i]，有了这些已知条件后，对于每个位置i，我们可以通过min(left_max[i], right_max[i]) - height[i]得到位置i的水柱高度。

完整代码如下：

class Solution:def trap(self, height: List[int]) -> int:if not height:return 0# 木桶理论# 对于位置i，left_max[i]记录的是其左侧最高柱子的高度left_max = [0] # 对于第0根柱子，其左侧没有柱子，默认其左侧最高柱子的高度为0# 对于位置n-1-i，right_max[i]记录的是其右侧最高柱子的高度right_max = [0] # 对于最后一根柱子，其右侧没有柱子，默认其右侧最高柱子的高度为0n = len(height)# 顺序遍历for i in range(1, n):# 对于位置i，left_max[-1]记录的是位置i-1其左侧最高柱子的高度---> 只需要和位置i-1的高度height[i-1]进行比较并取最大值即可得到位置i其左侧最高柱子的高度left_max.append(max(left_max[-1], height[i-1]))# 逆序遍历for i in range(n-2, -1, -1):# 对于位置i，right_max[-1]记录的是位置i+1其右侧最高柱子的高度---> 只需要和位置i+1的高度height[i+1]进行比较并取最大值即可得到位置i其右侧最高柱子的高度right_max.append(max(right_max[-1], height[i+1]))# 因为是逆序遍历，需要将结果反转 ---> 反转后, right_max[i]记录的是位置i其右侧最高柱子的高度right_max = right_max[::-1]# 获取每个位置i的水柱高度total_rain = 0for i in range(n):water_height = min(left_max[i], right_max[i]) - height[i] # 水柱高度计算公式(根据木桶原理)if water_height > 0: # 水柱高度大于0才有意义total_rain += water_heightreturn total_rain

运行结果：

复杂度分析

• 时间复杂度：O(N)，其中 N 是数组height元素的数量。
• 空间复杂度：O(N)
  • 需要存放每个位置左/右侧最高柱子的高度 ===> O(N)

结束语

• 亲爱的读者，感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见，因此在这里鼓励您对我们的博客进行评论。
• 您的建议和看法对我们来说非常重要，这有助于我们更好地了解您的需求，并提供更高质量的内容和服务。
• 无论您是喜欢我们的博客还是对其有任何疑问或建议，我们都非常期待您的留言。让我们一起互动，共同进步！谢谢您的支持和参与！
• 我会坚持不懈地创作，并持续优化博文质量，为您提供更好的阅读体验。
• 谢谢您的阅读！