目录
快速排序(hoare版本)
初级实现
问题改进
中级实现
时空复杂度
高级实现
三数取中
快速排序(hoare版本)
初级实现
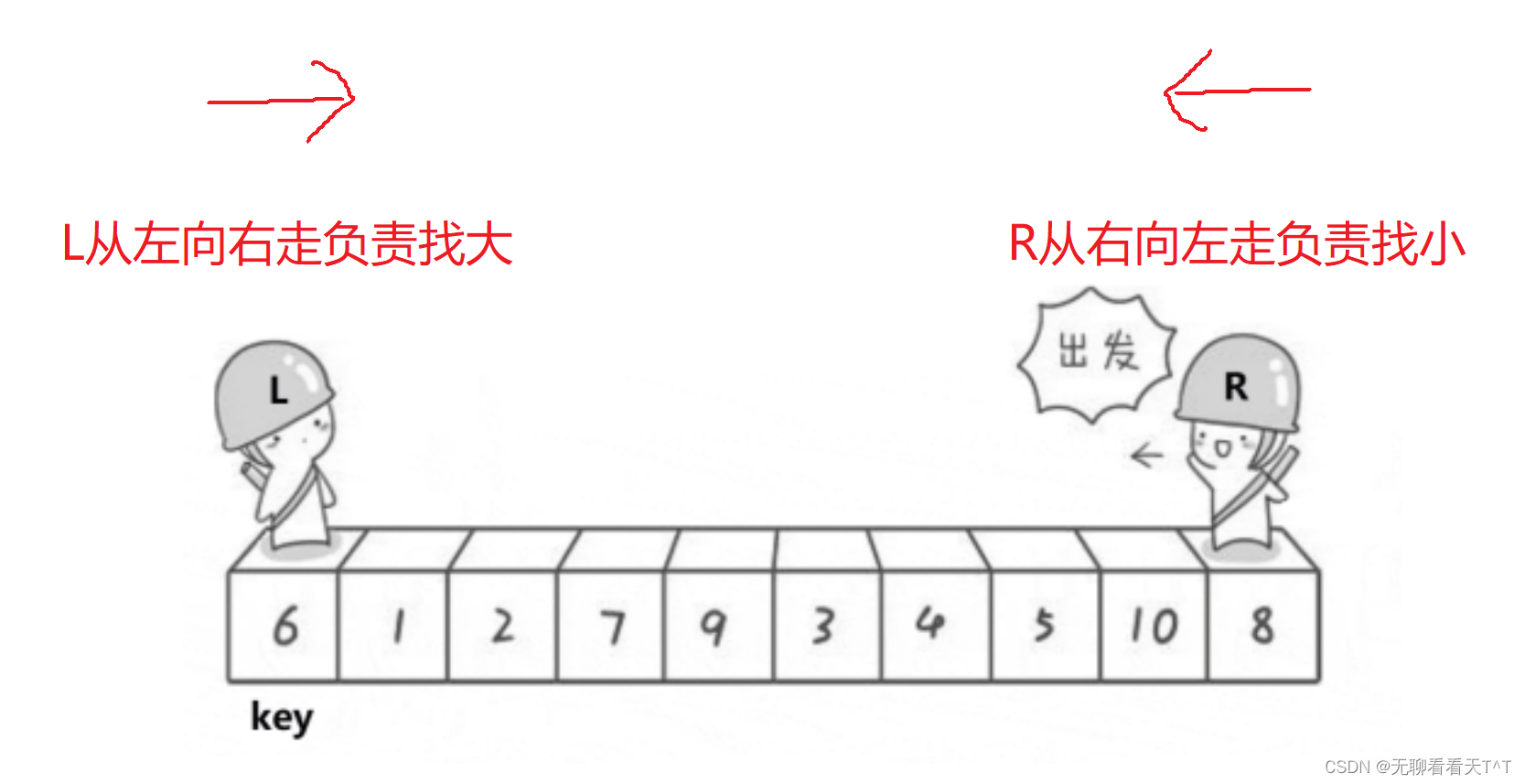
int left = begin; //数组首元素下标
int right = end; //数组尾元素下标
int keyi = begin; //即可以是首元素下标、也可以是尾元素下标,一般来说是首元素下标2、right和left开始自己的寻找任务,当a[right] > a[keyi],right就--继续向左走,当a[left] < a[keyi],left就++继续向右走,当二者都在找的过程中在某一位置停下时(两个while循环均结束),交换此时的a[left]和a[right]:
void QuickSort(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;// 右边找小while (a[right] > a[keyi]){--right;}// 左边找大while (a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}3、当left与right相遇即left == right时,此时元素的值一定小于基准元素的值,所以交换当前元素与基准元素的位置(因为我们要做的就是将小于基准元素的数放在左边,大于的放在右边):

void QuickSort(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (a[right] > a[keyi]){--right;}// 左边找大while (a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);
}关于“为什么相遇位置一定会比基准元素小”的解释:
因为我们规定右边先走(当然你也可以让左基准元素是数组尾元素然后左边先走,这里就不再分析了),这样就会有两种相遇的情况:
①right遇到left,right没找到比基准元素小的,一直走,找到时停下,然后left向右走,当二者相遇即right ==left时停下(原因我们后面会将),所处位置的元素的值小于基准元素:
②left遇到right,right先走,找到小于基准元素的位置停下,left开始找比基准元素大的,没有找到,一直走,遇到right停下,相遇位置是right,前面说过此时的位置应该是小于基准元素的位置(“right先走,找到小于基准元素的位置停下”):
至此,我们快速排序的初级实现已经完成了,接下来就是处理我们遗留的一些问题了:
问题改进
1、产生原因:有时我们写的代码只适用于部分数据,但是换成其它数据时就会出错,为了保证我们代码的通用性,我们要进行多次的用例测试,比如我们将数组换为{6,1,2,5,4,6,9,7,10,8}:
可以发现,之前的代码并不能让right和left相遇,又因为我们规定right先走,所以我们为了能让二者相遇,需要保证left永远不会超过right,故在a[right] > a[keyi]之前加上left < right,即left < right && a[right] >= a[keyi],left也是一样的道理:
void QuickSort(int* a, int begin, int end) {int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] > a[keyi]){--right;}// 左边找大while (left < right && a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]); }
2、产生原因:当我们将基准元素换到数组的中的某个位置时,它左侧的元素经过一系列检查与交换的操作后已经全部是小于基准元素的元素,右边的元素也已经全部是大于基准元素的元素,现在我们要做的就是将左右两边的元素均变为有序,当左右两边均有序时该数组就完全有序(原因自己想去😡)这就需要用到递归思想了(在前面我们说过hoare版本的快排是基于二叉树思想的),当我们尝试对上面的数组开始递归操作时,如果还是原来的代码就会出现下图所示的问题:
可以发现, 原本我们是想通过右递归将右侧大于基准元素的几个元素变为有序,但可以看到的是只有当a[right] == 4时才会停下,此时就已经在左递归的范围内了,因此为了保证不会越界,我们还需要为a[right] > a[keyi]加上一个"=",即a[right] >= a[keyi],左递归也是一样的道理:
void QuickSort(int* a, int begin, int end) {int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]); }
中级实现
至此,我们开始进行递归操作,关于递归的过程如下图所示:
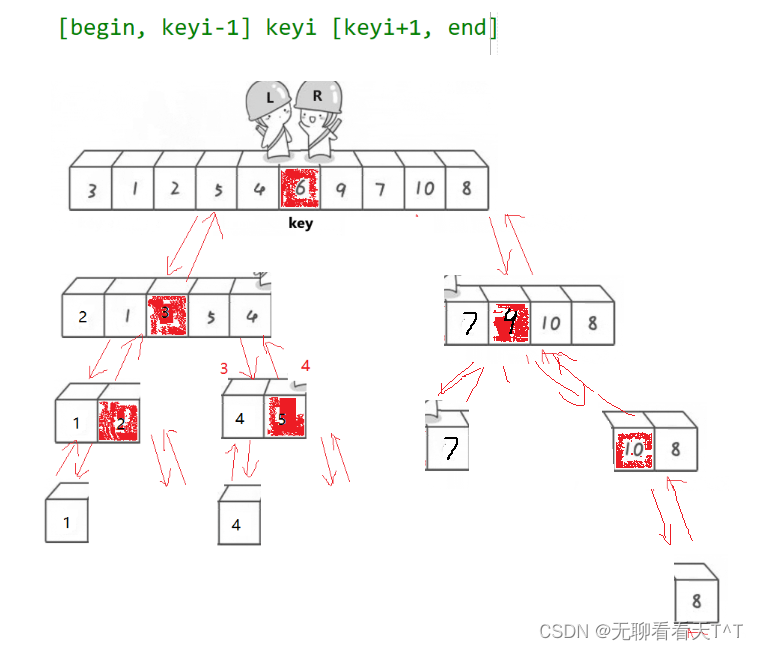
关于递归的代码也不再过多解释,自行理解即可:
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
以上就是一个“较为”完整的快速排序的代码
时空复杂度
最坏时间复杂度:O(N^2)(当数组已经降序有序或升序有序时,此时基准元素一直位于首元素或尾元素,n个元素要进行n次快速排序才能将当前的顺序改变,n*n)
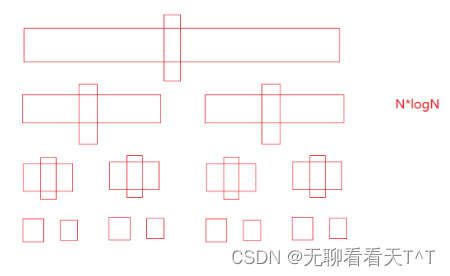
最好时间复杂度:O(N*logN)(每次划分都能将数组均匀地分成两个接近子数组,N个元素要进行logN次的排序,N*logN)
空间复杂度:O(logN)或O(N)(在递归过程中需要使用栈来保存函数调用信息,所以快速排序的空间复杂度取决于递归调用的层数。在最坏情况下,递归调用栈可能达到O(n)的空间复杂度,最好的空间复杂度为O(logn))
高级实现
当面对有序队列时,快速排序的效率确实会降低。这是因为快速排序的分区操作通常选择一个基准元素,并将小于等于基准的元素放在左侧,大于基准的元素放在右侧。如果输入数据已经有序,那么每次分区后只能将一个元素移到正确位置上,而剩余部分仍然需要进行递归调用。为了应对这种情况,可以采取以下方法来提高快速排序在有序队列上的效率:
随机化选择基准:通过随机选择基准值可以降低出现最坏情况(即已经有序)的概率。这样可以增加快速排序处理无序数据时的性能。
三数取中法:使用三数取中法来选择合适的基准值。从待排序数组中选取头、尾和中间位置上的三个数,并将它们按照大小顺序排列。然后选取其中位数作为划分子数组(即作为枢纽),以避免最坏情况发生。
插入排序优化:当待排序子数组长度较小时(比如小于某个阈值),可以切换到插入排序算法进行处理。插入算法对局部有序数据表现良好,在长度较短的子数组上可以提高排序效率。
优化递归调用:通过限制递归深度或者使用尾递归优化等方法,减少对有序数据的不必要处理。
这些方法可以在特定情况下提高快速排序算法在有序队列上的性能,但需要根据具体场景选择合适的策略。
三数取中
注意事项:获取的是下标为begin、midi、end的三个元素中的中位数(非最多,非最小)
完整代码如下:
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi; //返回a[midi] < a[midi] < a[end]else if (a[begin] > a[end])return begin; //返回a[end] < a[begin] < a[midi]elsereturn end; //返回a[begin] < a[end] < a[midi]}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi; //返回a[end] < a[mid] < a[begin]else if (a[begin] < a[end])return begin; //返回a[midi] < a[begin] < a[end]else return end; //返回a[midi] < a[end] < a[begin]}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}~over~










)

)


)

+数据集+模型(一))





- ACodec(四))
)