在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到 只包含 ‘1’ 的最大正方形，并返回其面积。

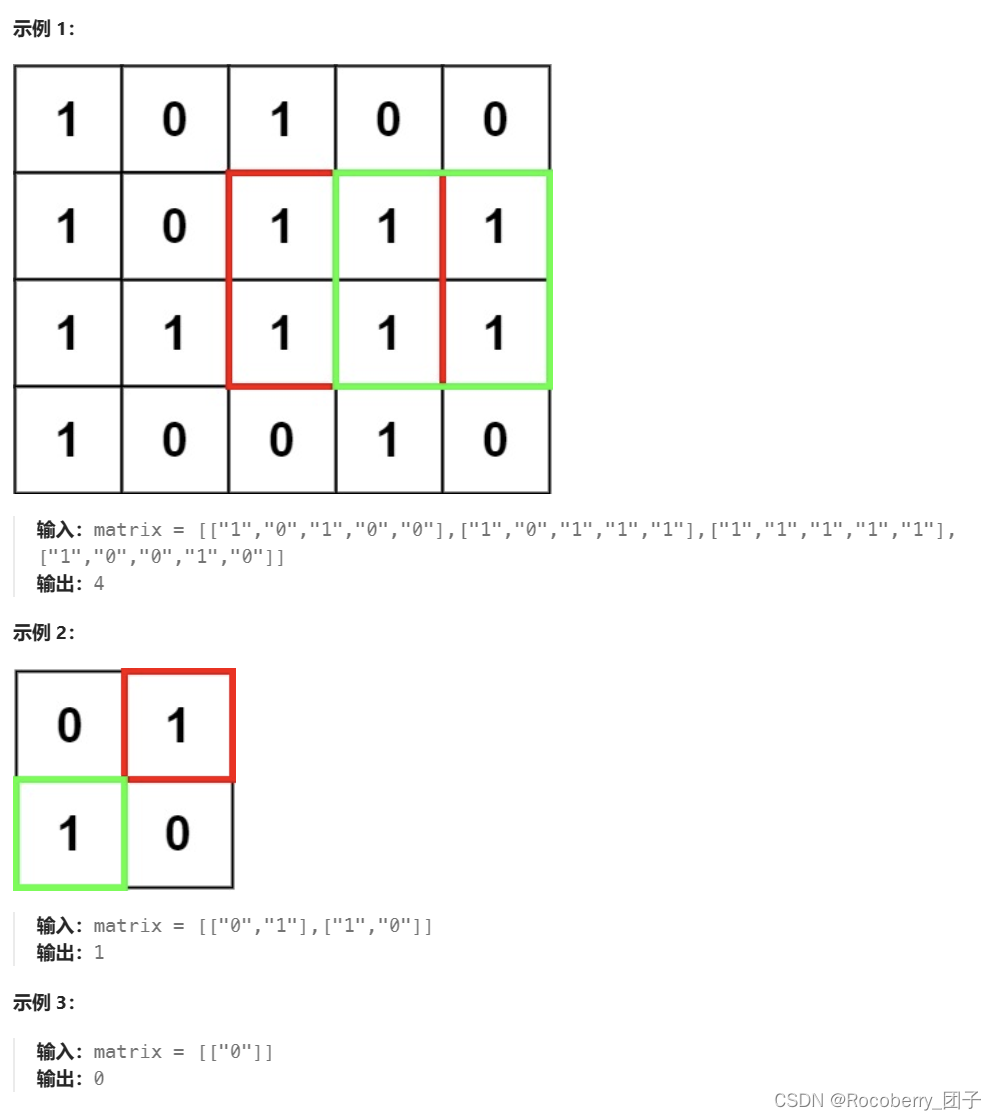
提示：

• m == matrix.length, n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 ‘0’ 或 ‘1’

题解1 DP

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int row = matrix.size(), col = matrix[0].size();// 定义：以 matrix[i][j] 为右下角元素的全为 1 正方形矩阵的最大边长为 dp[i][j]。vector<vector<int>> dp(row, vector<int>(col));// base casefor(int i = 0; i < row; i++){dp[i][0] = matrix[i][0] - '0';}for(int i = 0; i < col; i ++){dp[0][i] = matrix[0][i] - '0';}// dpfor(int i = 1; i < row; i++){for(int j = 1; j < col; j++){if(matrix[i][j] == '0') continue;// 木桶原理dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;}}int len = 0;for(int i = 0; i < row; i++){for(int j = 0; j < col; j++){len = max(len, dp[i][j]);}}return len*len;}
};

题解2 暴力(参考)

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {if (matrix.size() == 0 || matrix[0].size() == 0) {return 0;}int maxSide = 0;int rows = matrix.size(), columns = matrix[0].size();for (int i = 0; i < rows; i++) {for (int j = 0; j < columns; j++) {if (matrix[i][j] == '1') {// 遇到一个 1 作为正方形的左上角maxSide = max(maxSide, 1);// 计算可能的最大正方形边长int currentMaxSide = min(rows - i, columns - j);for (int k = 1; k < currentMaxSide; k++) {// 判断新增的一行一列是否均为 1bool flag = true;if (matrix[i + k][j + k] == '0') {break;}for (int m = 0; m < k; m++) {// 行 || 列 if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {flag = false;break;}}if (flag) {maxSide = max(maxSide, k + 1);} else {break;}}}}}int maxSquare = maxSide * maxSide;return maxSquare;}
};