LeetCode刷题--- 找出所有子集的异或总和再求和

个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

http://t.csdnimg.cn/yUl2I

【C++】

http://t.csdnimg.cn/6AbpV

数据结构与算法

http://t.csdnimg.cn/hKh2l

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

找出所有子集的异或总和再求和

题目链接：找出所有子集的异或总和再求和

题目

一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果；如果数组为空，则异或总和为 0 。

例如，数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。

给你一个数组 nums ，请你求出 nums 中每个子集的 异或总和 ，计算并返回这些值相加之和。

注意：在本题中，元素相同的不同子集应多次计数。

数组 a 是数组 b 的一个子集的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

示例 1：

输入：nums = [1,3]
输出：6
解释：[1,3] 共有 4 个子集：
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6

示例 2：

输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

示例 3：

输入：nums = [3,4,5,6,7,8]
输出：480
解释：每个子集的全部异或总和值之和为 480 。

提示：

1 <= nums.length <= 12
1 <= nums[i] <= 20

解法

题目解析

给你一个数组 nums ，请你求出 nums 中每个子集的 异或总和 ，计算并返回这些值相加之和。

输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

算法原理思路讲解

所有⼦集可以解释为：每个元素选择在或不在⼀个集合中（因此，⼦集有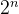 $2^{n}$ 个）。本题我们需要求出所有⼦集，将它们的异或和相加。因为异或操作满⾜交换律，所以我们可以定义⼀个变量，直接记录当前状态的异或和。使⽤递归保存当前集合的状态（异或和），选择将当前元素添加⾄当前状态与否，并依次递归数组中下⼀个元素。当递归到空元素时，表⽰所有元素都被考虑到，记录当前状态（将当前状态的异或和添加⾄答案中）

一、画出决策树

决策树就是我们后面设计函数的思路

二、设计代码

（1）全局变量

int ret;     // 存储异或后的结果
int path;    // 记录路径中子集的状态

（2）设计递归函数

void dfs(vector<int>& nums, int pos);

递归流程如下

在递归过程中，对于每个元素，我们只能向后选择：
1. 将 path 中子集的异或的结果计入 ret
2. 选择当前元素，将其异或，然后在递归结束时再次异或（也即是回溯）
但递归结束，所有符合条件的状态都被记录下来了

代码实现

时间复杂度：O( $2^{n}$ )，，其中 n 为 nums 的长度
空间复杂度：O(n)，即为递归时的栈空间开销。

class Solution 
{int ret;int path;
public:void dfs(vector<int>& nums,int pos){ret += path;for (int i = pos; i < nums.size(); ++i){path ^= nums[i];dfs(nums,i+1);path ^= nums[i];         //回溯}}int subsetXORSum(vector<int>& nums) {dfs(nums,0);return ret;}
};