- {
}公差大于零的等差数列:多个数字组成的数列,两两之间差相等,且后值减前值大于0,如:{-2,0,2,4}为公差数列为2的等差数列.
- 因数是指整数a除以整数b(b≠0) 的商正好是整数而没有余数,10的因数为 2和5
- 圆柱体表面积
=2πr² + 2πrh
- 球体表名面积
= 4πR²
- 圆周长 C = 2πr
- 矩形面积为边长相乘,S = x * y
- 等腰三角形面积 =
* 腰* 腰* sinC夹角;s=
底*高。
- 等腰直角三角形面积 =
* a腰 * b腰
- 勾股定理指直角三角形的两条直角边的平方和等于斜边的平方,c² = a²+b²
- sin45°=
; sin30=
; sin60=
- 扇形面积公式 ABO = C * π * a² ÷ 360
- 一元二次方程求解
- 对于一个二次方程 ax²+ bx + c = 0,其判别式 b² - 4ac决定了该方程的根的性质。判别式的值决定了方程的解的类型:
- 1. 如果 b² - 4ac> 0 ,则方程有两个不相等的实数根。
- 2. 如果 b² - 4ac = 0 ,则方程有两个相等的实数根(重根)
- 3. 如果 b² - 4ac < 0 ,则方程没有实数根,而是有两个共轭的复数根。
- 方差:
- 根据完全平方公式(a+b)²=a²+2ab+b²、(a-b)²=a²-2ab+b²
- 组合排列公式
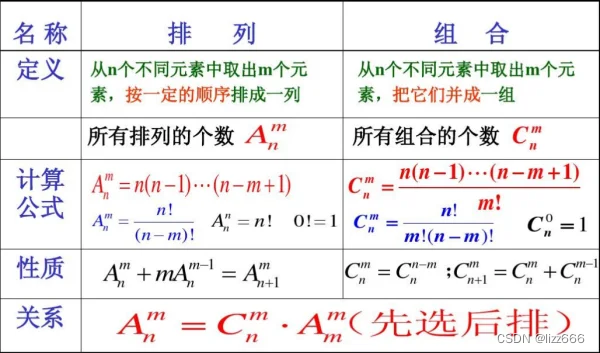
MBA-数学题概念和公式
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/226137.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
生产环境_Apache Spark技术大牛的实践:使用DataFrame API计算唯一值数量并展示技术(属性报告)
业务背景 给前端提供算法集成好的数据,对算法处理后的数据进行进一步删选展示 可以使用下面代码运行一下看看结果,听有趣的,我写的代码中计算了不同字段的值的数量,并生成了一个显示字符串来描述这些数据的分布情况然后使用"…
MySQL数据库 DDL
目录
一、DDL
二、操作数据库
三、操作表
四、数据类型
五、表操作案例
六、修改表
七、删除表 一、DDL Data Definition Language,数据定义语言,用来定义数据库对象(数据库,表,字段) 。 二、操作数据库
(1&am…
微信小程序:按钮禁用,避免按钮重复提交
wxml
<view class"modal-buttons"><view class"one_btn" bindtap"submit">确认</view><view class"two_btn" bindtap"cancel">取消</view>
</view>
wxss
/* 按钮 */
.modal-buttons…
maven 引入外部jar包
有时依赖的第三方jar不在maven仓库中,为了能按照maven的方式管理jar同时方便成员间协同,可使用如下方式
在pom.xml同级目录下新建lib文件夹,然后将jar放入,然后纳入版本管理在pom.xml中配置依赖,比如
<dependency…
Rxjs 学习笔记 - 简化版
RxJS 提供了一套完整的异步解決方案,让我们在面对各种异步行为(Event, AJAX, Animation 等)都可以使用相同的 API 做开发。 前置知识点 同步(Synchronous)就是整个处理过程顺序执行,当各个过程都执行完毕,并返回结果。是一种线性执行的方式,执行的流程不能跨越。一般用…
Git 使用教程(超级详细)
目录
一:Git二:SVN与Git的的区别三、安装Git四:常规操作五:远程仓库六:创建与合并分支七:bug分支八:多人协作九:git可视化工具 Git
Git 是一种分布式版本控制系统,用于…
C# WPF上位机开发(加密和解密)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 在报文传输的过程中,根据报文传输的形态,有两种形式,一种是明文传输,一种是加密传输。当然明文传输…
Python+Requests+Pytest+YAML+Allure实现接口自动化
本项目实现接口自动化的技术选型:PythonRequestsPytestYAMLAllure ,主要是针对之前开发的一个接口项目来进行学习,通过 PythonRequests 来发送和处理HTTP协议的请求接口,使用 Pytest 作为测试执行器,使用 YAML 来管理测…
Git使用rebase和merge区别
Git使用rebase和merge区别 模拟环境使用merge合并使用rebase 模拟环境
本地dev分支中DevTest增加addRole() 远程dev被同事提交增加了createResource()
使用merge合并
使用idea中merge解决冲突后, 推送远程dev后,日志图显示
使用rebase
idea中使用功能rebase 解决冲突…
kafka3.0创建topic出现zookeeper is not a recognized option
在linux云服务器上搭建了一套kafka3.0集群,然后安装以前的创建topic指令,例如这样——
./kafka-topics.sh --bootstrap-server master:2181,slave1:2181,slave2:2181 --replication-factor 1 --partitions 1 --topic test
然而,却出现了这样…
C语言中的文件压缩和解压缩技术是什么?
文件压缩和解压缩是计算机领域中常用的技术,通过压缩可以减小文件的体积,从而更高效地存储和传输数据。在C语言中,有多种文件压缩和解压缩的技术和算法可供选择。本文将介绍一些常见的压缩和解压缩技术,以及在C语言中如何实现它们…
【正点原子STM32连载】 第十五章 窗口看门狗实验 摘自【正点原子】APM32E103最小系统板使用指南
1)实验平台:正点原子APM32E103最小系统板 2)平台购买地址:https://detail.tmall.com/item.htm?id609294757420 3)全套实验源码手册视频下载地址: http://www.openedv.com/docs/boards/xiaoxitongban
第十…
代码随想录——链表 刷题记录
链表数据结构
public class ListNode {int val;ListNode next;// 构造函数public ListNode() {}public ListNode(int val) {this.val val;}public ListNode(int val, ListNode next) {this.val val;this.next next;}
}203.移除链表元素
707.设计链表
单链表双链表
publi…
遥感图像分割系统:融合空间金字塔池化(FocalModulation)改进YOLOv8
1.研究背景与意义
项目参考AAAI Association for the Advancement of Artificial Intelligence
研究背景与意义
遥感图像分割是遥感技术领域中的一个重要研究方向,它的目标是将遥感图像中的不同地物或地物类别进行有效的分割和识别。随着遥感技术的不断发展和遥感…
Hystrix使用及原理概述
一、背景
1. 当前问题
一个系统,所有请求共用同一个APP容器(Tomcat/jetty/等),共用一个用户线程池,依赖多个不同的远程服务。
当系统健康时,处理请求的延时较低,服务正常运行;当某…
大模型下开源文档解析工具总结及技术思考
1 基于文档解析工具的方法
pdf解析工具
导图一览: PyPDF2提取txt: import PyPDF2
def extract_text_from_pdf(pdf_path):with open(pdf_path, rb) as file:pdf_reader PyPDF2.PdfFileReader(file)num_pages pdf_reader.numPagestext ""f…
漏洞复现-网神SecGate3600防火墙敏感信息泄露漏洞(附漏洞检测脚本)
免责声明
文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…
记录 | ubuntu安装Albert
ubuntu 安装 Albert
# 依赖安装
sudo apt install cmake pybind11-dev libmuparser-dev libqalculate-dev libxcb-cursor0 libgl1-mesa-dev# 安装Qt6git clone --recursive https://github.com/albertlauncher/albert.gitcd albert
# 若 albert/plugin clone失败,则…
算法leetcode|92. 反转链表 II(rust重拳出击)
文章目录 92. 反转链表 II:样例 1:样例 2:提示:进阶: 分析:题解:rust:go:c:python:java: 92. 反转链表 II:
给你单链表的…
)




)
)







改进YOLOv8)


)

)