继续看回溯问题

关卡名	继续看回溯问题	我会了✔️
内容	1.复习递归和N叉树，理解相关代码是如何实现的	✔️
内容	2.理解回溯到底怎么回事	✔️
	3.掌握如何使用回溯来解决二叉树的路径问题	✔️

1 复原IP地址

这也是一个经典的分割类型的回溯问题。LeetCode93.有效IP地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。
例如："0.1.2.201" 和 "192.168.1.1" 是有效 IP 地址，但是 "0. 011. 255 .245"、"192.168.1.312" 和 "192.168@1.1" 是无效IP地址。给定一个只包含数字的字符串s，用以表示一个IP地址，返回所有可能的有效IP地址，这些地址可以通过在s中插入 '.' 来形成。你不能重新排序或删除s中的任何数字。你可以按任何顺序返回答案。

示例1：

输入：s = "25525511135"

输出：["255.255.11.135","255.255.111.35"]

该问题的思路与与前面的分割回文串基本一致，也是切割问题。回溯的第一步就是使用枚举将所有可能性搜出来,找到一个符合要求的就先切下来，后面的部分继续进行枚举和切割，如果到了最后发现不符合要求，则开始回溯。
本题的难度明显比上一题要大，主要是判断是否合法的要求更高了，比如第一个元素我们可以截取2、25、255、2552，很显然到了2552之后就不合法了，此时就要回溯。后面也一样，假如我们第一层截取的是2，第二层就从”5525511135“中截取，此时可以有5，55，552，显然552已经不合法了，依次类推。画出图来就如下所示：

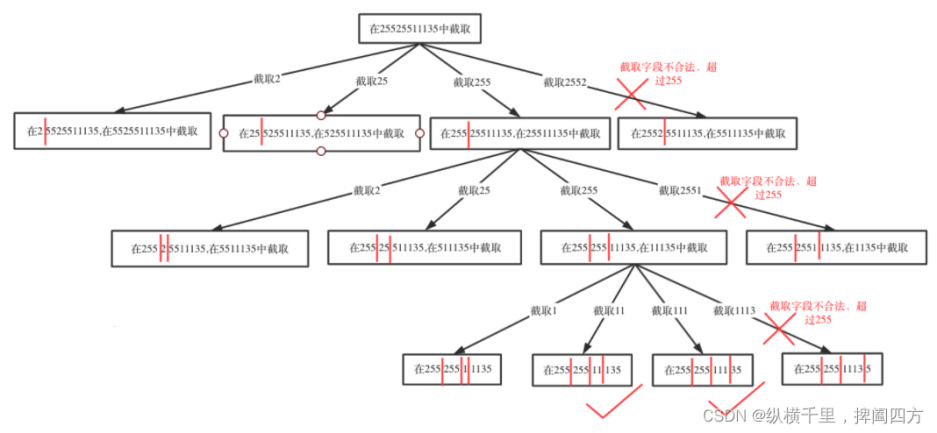
当然这里还要判断是0的情况等等，在字符串转换成数字一章，我们讲解了很多种要处理的情况，为此我们可以写一个方法单独来执行相关的判断。代码如下：

// 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法private Boolean isValid(String s, int start, int end) {if (start > end) {return false;}// 0开头的数字不合法if (s.charAt(start) == '0' && start != end) { return false;}int num = 0;for (int i = start; i <= end; i++) {// 遇到⾮数字字符不合法if (s.charAt(i) > '9' || s.charAt(i) < '0') { return false;}num = num * 10 + (s.charAt(i) - '0');if (num > 255) { // 如果⼤于255了不合法return false;}}return true;}

另外，IP地址只有四段，不是无限分割的，因此本题只会明确的分成4段，不能多也不能少。所以不能用切割线切到最后作为终止条件，而是分割的段数到了4就必须终止。考虑到我们构造IP地址时还要手动给添加三个小数点，所以我们用变量pointNum来表示小数点数量，pointNum为3说明字符串分成了4段了。
要手动添加一个小数点，这要增加一个位置来存储，所以下一层递归的startIndex要从i+2开始。其他的主要工作就是递归和回溯的过程了。这里的撤销部分要注意将刚刚加入的分隔符删掉，并且pointNum也要-1，完整代码如下：

class RestoreIpAddresses {List<String> result = new ArrayList<>();public List<String> restoreIpAddresses(String s) {//这个是IP的特性决定的if (s.length()<4||s.length() > 12) return result; backTrack(s, 0, 0);return result;}// startIndex: 搜索的起始位置， pointNum:添加小数点的数量private void backTrack(String s, int startIndex, int pointNum) {if (pointNum == 3) {// 小数点数量为3时，分隔结束// 判断第四段⼦字符串是否合法，如果合法就放进result中if (isValid(s,startIndex,s.length()-1)) {result.add(s);}return;}for (int i = startIndex; i < s.length(); i++) {if (isValid(s, startIndex, i)) {//在str的后⾯插⼊⼀个小数点s = s.substring(0, i + 1) + "." + s.substring(i + 1);    pointNum++;// 插⼊小数点之后下⼀个⼦串的起始位置为i+2backTrack(s, i + 2, pointNum);pointNum--;// 撤销操作s = s.substring(0, i + 1) + s.substring(i + 2);//撤销操作} else {break;}}}
}

2 电话号码问题

LeetCode17.电话号码组合问题，也是热度非常高的一个题目，给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母，9对应四个字母。

示例1：

输入：digits = "2| 3 4567"

输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

我们说回溯仍然会存在暴力枚举的情况，这个题就很典型，例如如果输入23，那么，2就有 a、b、c三种情况，3有d、e、f三种情况。组合一下就一共就有3*3=9种，如果是233，那么就是27种。
这里要注意的9对应4个字母，而1则没有，那该怎么建立字母和数字之间的映射呢？我们用一个数组来保存，而不写一堆的if else。而为了保证遍历时index也恰好与数组的索引一致，我们按照如下的方式来定义数组：
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
接下来我们就用回溯来解决n层循环的问题，输入23对应的树就是这样的：

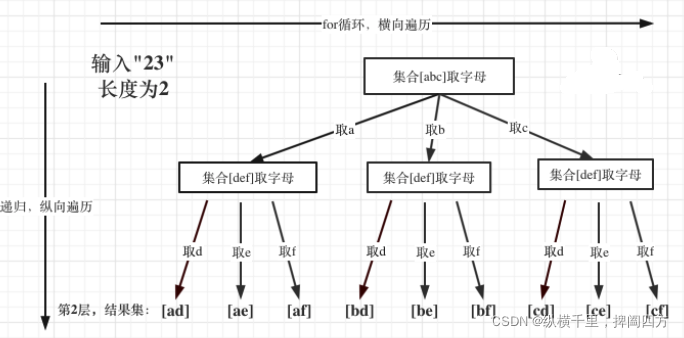树的深度就是输入的数字个数，例如输入23，树的深度就是2。而所有的叶子节点就是我们需要的结果["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。所以这里的终止条件就是，如果当前执行的index 等于输入的数字个数（digits.size）了。
使用for循环来枚举出来，然后循环体内就是回溯过程了。基本实现过程如下：

class LetterCombinations {List<String> list = new ArrayList<>();public List<String> letterCombinations(String digits) {if (digits == null || digits.length() == 0) {return list;}//初始对应所有的数字，为了直接对应2-9，新增了两个无效的字符串""String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};backTracking(digits, numString, 0);return list;}//每次迭代获取一个字符串，所以会设计大量的字符串拼接，所以这里选择更为高效的 StringBuildStringBuilder temp = new StringBuilder();//比如digits如果为"23",num 为0，则str表示2对应的 abcpublic void backTracking(String digits, String[] numString, int num) {//遍历全部一次记录一次得到的字符串if (num == digits.length()) {list.add(temp.toString());return;}//str 表示当前num对应的字符串String str = numString[digits.charAt(num) - '0'];for (int i = 0; i < str.length(); i++) {temp.append(str.charAt(i));backTracking(digits, numString, num + 1);//剔除末尾的继续尝试temp.deleteCharAt(temp.length() - 1);}}
}

3 括号生成问题

本题是一道非常典型的回溯问题，LeetCode22.数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例1：

输入：n = 3

输出：["((()))","(()())","(())()","()(())","()()()"]

要解决该问题，我们首先要明确一个问题，左右括号什么时候可以获得。我们知道左括号出现的数量一定等于n，观察题目给的示例，只要剩余左括号的数量大于0，就可以添加"("，例如"("、"(()"、”(()(“、”()((“都是可以的，因为我们只要再给加几个右括号就行，例如可以将其变成"()"、"(())"、”(()()“、”()(())“。
那添加右括号的要求呢？结论是：序列中左括号的数量必须大于右括号的数量，例如上面的"("、"(()"、”(()(“、”()((“，都可以，但是如果")"、"())"、”)()(“、”()((“就不可以了，此时的情况都是右括号数量大于等于左括号。所以我们可以得到两条结论：

1.只要剩余左括号的数量大于0，就可以添加"("。
2.序列中左括号的数量必须大于右括号的数量才可以添加"("，并且")"的剩余数量大于0。

接下来看如何用回溯解决，我们将添加"("视为left，将")"视为right，这样"("和")"各可以出现n次。我们以n=2为例画一下的图示：

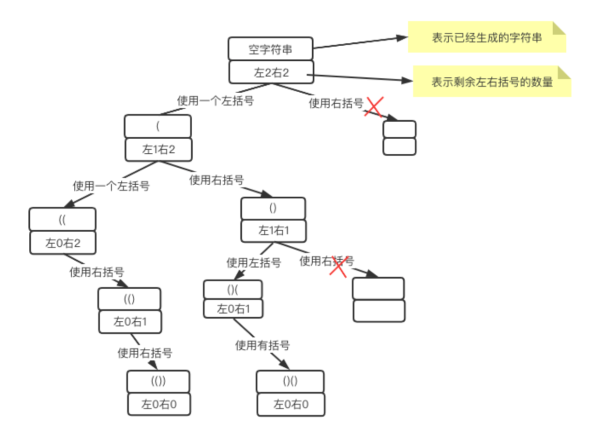
图中红叉标记的位置是左括号大于有括号了，不能再向下走了，这个操作也称为剪枝。通过图示，可以得到如下结论：

当前左右括号都有大于 0 个可以使用的时候，才产生分支，否则就直接停止。
产生左分支的时候，只看当前是否还有左括号可以使用；
产生右分支的时候，除了要求还有右括号，还要求剩余右括号数量一定大于左括号的数量；
在左边和右边剩余的括号数都等于 0 的时候结束。

而且，从上图可以看到，不管是剪枝还是得到一个结果，返回的过程仍然可以通过回溯来实现：

class GenerateParenthesis {public List<String> generateParenthesis(int n) {List<String> ans = new ArrayList<String>();backtrack(ans, new StringBuilder(), 0, 0, n);return ans;}/*** @param ans 当前递归得到的结果* @param cur 当前的括号串* @param open   左括号已经使用的个数* @param close  右括号已经使用的个数* @param max    序列长度最大值*/public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {if (cur.length() == max * 2) {ans.add(cur.toString());return;}//本题需要两次回溯，比较少见的情况if (open < max) {cur.append('(');backtrack(ans, cur, open + 1, close, max);cur.deleteCharAt(cur.length() - 1);}if (close < open) {cur.append(')');backtrack(ans, cur, open, close + 1, max);cur.deleteCharAt(cur.length() - 1);}}
}