day13
2023.12.11
代码随想录
今天刚出差回来，拉下了很多天的博客，慢慢补吧，每天做当天的任务，再补一篇博客。

1. 239滑动窗口最大值
本题就是每次窗口内容放在一个单调队列中，那么每次直接返回队头元素（最大值）即可，在删一个元素以及填一个元素。所以关键就是这个单调队列怎么创建，以及每次滑动该队列元素怎么变化。
首先就是创建单调队列，实际我们要维护的单调队列内容并不包括所有窗口的元素，例如{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 。保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。创建该队列要求是，每次增加元素要小于队尾元素，即满足单调。如果大于队尾元素，将队尾元素弹出。比如。先增加2，再增加3时，要增加的3>队尾元素2，因此弹出2，增加3。增加5同理，增加1时，1小于队尾元素5，正常添加。。。如此往下
单调队列创建后，就要随窗口滑动不断更新，如果滑动窗口要弹出的值==队头元素（即为最大值），则需要改变单调队列。弹出队头元素即可。如果不等于，则表示这次窗口滑动删掉的元素不影响新的单调队列，因此单调队列不用改变，这是滑动删除的元素。滑动也会增加一个元素，增加元素后要保证队列仍是单调队列。同创建队列的要求。
每次窗口滑动满足上述要求，则每次滑动只需要返回队头元素即可，添加到一个结果数组即可。

class Solution {
private:class MyQueue{public:deque<int> que;void pop(int value){//每次将窗口删除的元素传给队列,等于队头，则弹出队头if(!que.empty() && value == que.front()){que.pop_front();}}void push(int value){while(!que.empty() && value>que.back()){que.pop_back();}que.push_back(value);}int front(){return que.front();}};
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue que;vector<int> result;for(int i=0;i<k;i++){que.push(nums[i]);}result.push_back(que.front());for(int i=k;i<nums.size();i++){que.pop(nums[i-k]);que.push(nums[i]);result.push_back(que.front());}return result;}
};

2. 347前K个高频元素
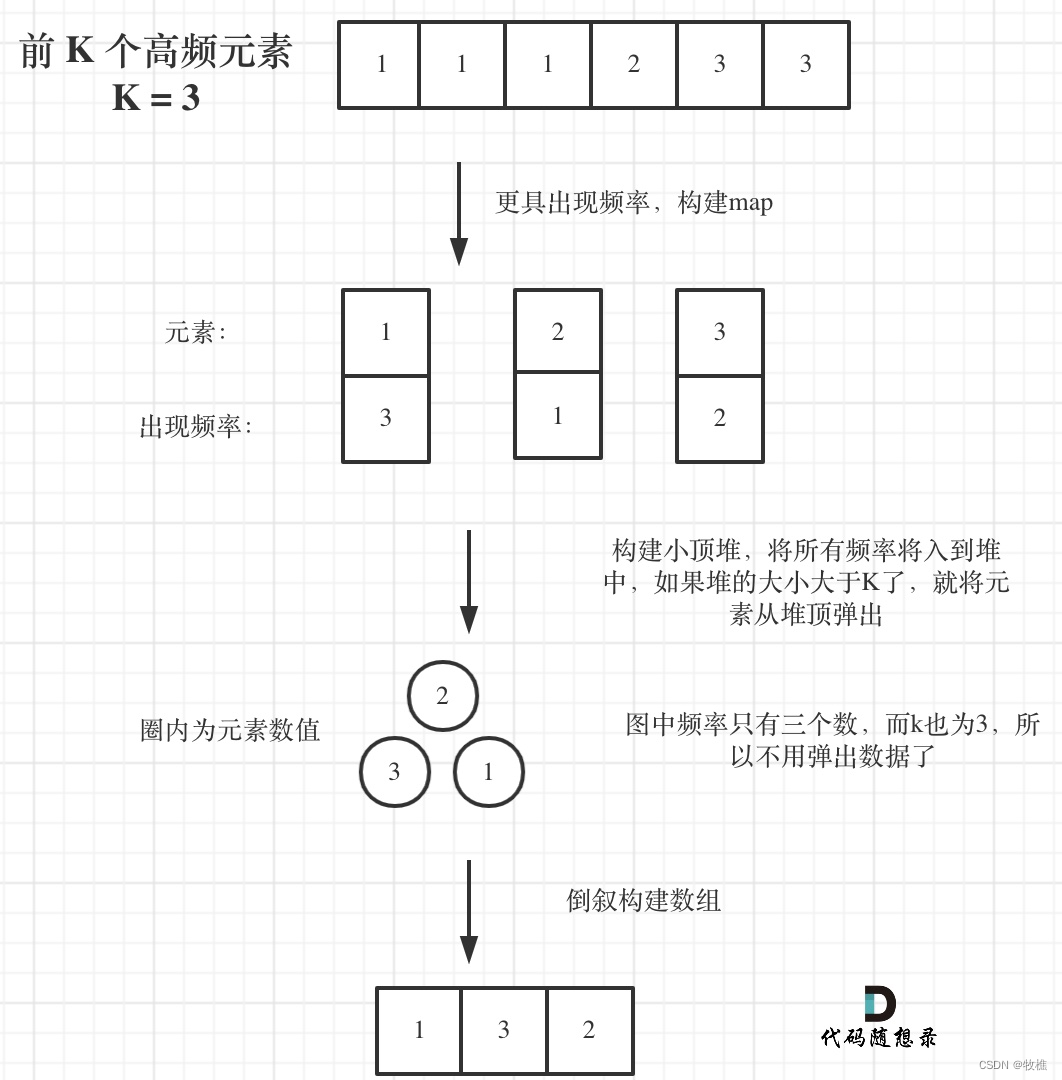
今天两道题难度都挺高的。所以都是直接看文字解释的。首先统计每个元素出现的频率，想到的就是map。再根据map的value，也就是频率构建小根堆。这些概念很熟悉，但却没写过相应的代码，因此这次理解起来还可以，但对于代码不是很熟悉。慢慢来吧。保证小根堆大小为k，每次删除头（最小频率），则遍历完后最后的小根堆就是要的k个频率最大的值。

class Solution {
public:// 小顶堆class mycomparison {public:bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {return lhs.second > rhs.second;}};vector<int> topKFrequent(vector<int>& nums, int k) {// 要统计元素出现频率unordered_map<int, int> map; // map<nums[i],对应出现的次数>for (int i = 0; i < nums.size(); i++) {map[nums[i]]++;}// 对频率排序// 定义一个小顶堆，大小为kpriority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;// 用固定大小为k的小顶堆，扫面所有频率的数值for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {pri_que.push(*it);if (pri_que.size() > k) { // 如果堆的大小大于了K，则队列弹出，保证堆的大小一直为kpri_que.pop();}}// 找出前K个高频元素，因为小顶堆先弹出的是最小的，所以倒序来输出到数组vector<int> result(k);for (int i = k - 1; i >= 0; i--) {result[i] = pri_que.top().first;pri_que.pop();}return result;}
};