本讲我们完成对“正交”的介绍。Gram-Schmidt 过程可以将原空间的一组基转变为标准正交基。

正交向量 Orthonormal vectors

满足如下条件的向量 q1，q2……qn为标准正交：
$$q_i^T{q}_j=\{\begin{array}{l}0,若x\ne j\\ 1,若x=j\end{array}$$

换而言之，它们都具有单位长度 1，并且彼此正交。标准正交向量是线性无关的。很多线性代数的计算都建立在标准正交基础上，它让一切变得简单可控。

标准正交矩阵 Orthonormal matrix

如果矩阵 Q 的列向量为标准正交向量，则 $Q^T$Q=I 为单位阵。

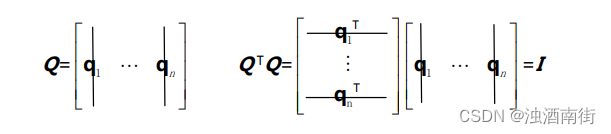
注意这里的矩阵 Q 可以不是方阵。我们已经学过了一系列矩阵，包括三角阵、对角阵、置换矩阵、对称矩阵、行最简梯形矩阵、投影矩阵等等，现在有了“标准正交”矩阵。
一个标准正交的方阵我们称之为“正交矩阵”（orthogonal matrix）。如果 Q为方阵，因为 Q TQ=I，所以 Q T=Q-1。注意必须是方阵，必须是标准正交，而不只是正交。

标准正交列向量的优势 Orthonormal columns are good

若 Q 的列向量为标准正交向量，则投影到 Q 的列空间的投影矩阵为： P=$Q(Q^{T}Q{)}^{-1}{Q}^T$
因为 Q TQ=I，所以 P=$Q{Q}^T$。这种情况会降低很多运算量。如果 Q 为方阵，则 P=I，因为 Q 的列向量张成了整个空间，投影过程不会对向量有任何改变。

施密特正交化 Gram-Schmidt

从两个线性无关的向量 a 和 b 开始，它们张成了一个空间，我们的目标是希望找到两个标准正交的向量 q1，q2 能张成同样的空间。Schmidt 给出的结论是如果我们有一组正交基 A 和 B，那么我们令它们除以自己的长度就得到标准正交基：
$$q_1=\frac{A}{\Vert \begin{array}{c}A\end{array}\Vert }{q}_2=\frac{B}{\Vert \begin{array}{c}B\end{array}\Vert }$$

Gram 做了重要的工作，令 A=a，我们在 a 和 b 张成的空间中，取与 A 正交向量做成标准正交基，方法就是将 b 投影到 a 的方向，然后取 B=b-p（B 就是之前谈论过的误差 e 的方向）。

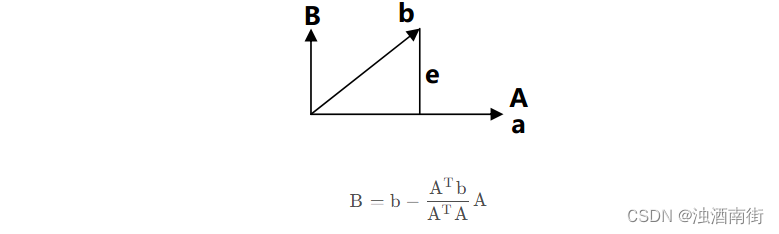
注意这个小节中 A，B，C 均为向量。
如果从等式两端左乘$A^T$，可以得到 $A^T$ B = 0 。
如果从三个线性无关的向量 a、 b 和 c 出发，则可以通过从 c 中减去其在 A 和B两个方向的投影来得到C。

Q的列空间与A的列空间是什么关系呢？它们是同一个列空间。
在消元过程中，我们可以对矩阵进行分解得到A =LU，而在对A 做施密特正交化的过程也可以用矩阵运算的方式表示为A = QR。此处R 为上三角阵。

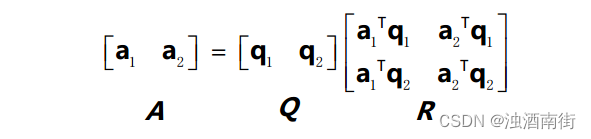
R 为上三角阵，则 $a_1^T{q}_2$=0。这是因为 a1就是 q1的方向，而 q1和 q2为标准正交向量，因此 q2的方向与 a1垂直，因此内积为 0。R 在 Q 右侧相当于对 Q 做列操作，即 A 的列向量是 Q 列向量的线性组合，而 Q 为 A 列空间的一组标准正交基，则 R 的元素实际上是 A 的列向量基于 Q 这组标准正交基的权。
采用矩阵的 QR 分解来帮助求解 Ax=b 的问题，最大的优势是提高了数值的稳定性。