流体和刚体的关系？

刚体仿真关注刚性物体的运动和力学行为。刚体是指在外力作用下保持形状和结构不变的物体，不受弯曲或拉伸的影响。刚体仿真基于刚体力学原理和刚体运动学方程，模拟刚体的运动、转动、碰撞等行为。它可以用于模拟刚体之间的物理交互、刚体的受力分析和结构设计等。刚体仿真在工程、动画、游戏开发等领域中得到广泛应用。
流体仿真主要关注液体或气体等流体在不同条件下的运动和性能。它基于流体力学原理和数值计算方法，通过建立数学模型和求解流体力学方程，预测流体的速度、压力、温度等参数，并分析其流动特性、湍流行为、压力分布等。流体仿真常用于工程领域，如汽车空气动力学、航空航天气动力学、水力学等。

什么是流体仿真？他能带来什么价值？

流体仿真是一种工程分析方法，用于模拟和预测液体或气体在不同条件下的流动行为和性能。它基于流体力学原理和数值计算技术，通过数学模型和计算方法对流体的运动、压力、温度等参数进行建模和求解。

流体仿真可以应用于各种流体系统的分析和优化，包括气体流动、液体流动、空气动力学、热传导、湍流等。它在各个领域中带来了许多价值和应用：

1. 设计优化：流体仿真可以帮助工程师进行产品设计的优化。通过模拟和分析不同设计方案下的流体行为，例如风阻、液体流动速度、温度分布等，可以评估不同设计参数对性能的影响，从而优化产品的外形、流体动力学特性和热传导性能。
2. 性能预测：流体仿真可以预测流体系统的性能和行为。例如，在汽车工程中，可以通过仿真分析车辆的空气动力学性能，如阻力系数、升力和气流分布，为改进燃油效率、降低噪音和提高稳定性提供指导。
3. 系统优化：流体仿真可以用于优化流体系统的运行和效率。通过模拟和分析管道、泵站、换热器等流体系统的流动特性，可以优化管道布局、减少能量损失、改进流体输送效率，从而提高系统的运行效果和能源利用率。
4. 故障排除和优化：流体仿真可以用于识别和解决流体系统中的问题和故障。通过模拟和分析流体系统的流动、压力和温度分布，可以检测潜在的设计缺陷、堵塞或泄漏等问题，并提供改进方案和优化建议。
5. 新产品开发和创新：流体仿真为工程师和设计师提供了更多的创新空间。它可以用于评估新产品或新技术的可行性和性能，为创新提供支持和指导。例如，在航空航天领域，流体仿真可以用于评估新型飞机翼型或涡轮引擎设计的性能和安全性。
6. 节约时间和成本：流体仿真可以减少试验的数量和成本。通过在计算机中进行仿真分析，可以更快速地评估和比较多个设计方案，避免实际试验的时间和费用，提高产品开发的效率。
   总体而言，流体仿真在工程领域中具有广泛的应用和价值。它能够提供准确的流体行为预测和优化，帮助改进产品设计、优化系统性能、降低成本，并推动工程创新和发展。

模拟流体仿真运动的原理是什么？

• 定义几何和边界条件：首先需要定义流体仿真的几何形状和边界条件。几何形状包括流体域的形状、流体体积和物体的几何形态，边界条件包括入口条件、出口条件和物体表面的边界条件。

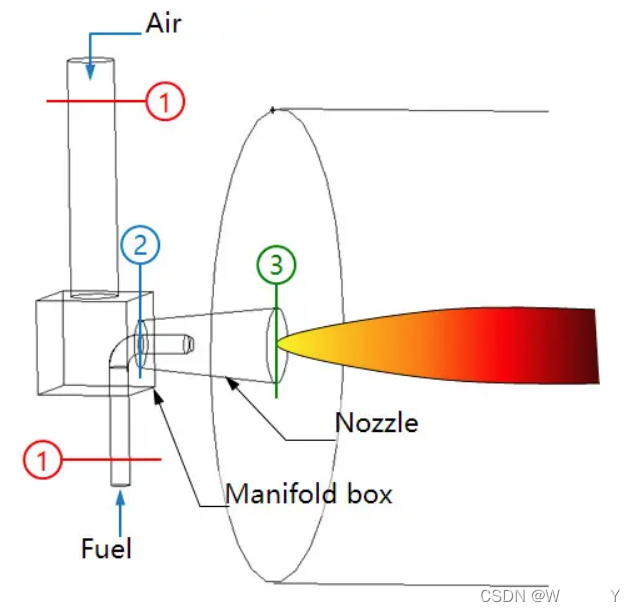
• 【在流体力学中的守恒方程中，通常大家第一个讨论的就是连续性方程，这个方程从某种意义上来讲，也可以认为是流体区别于固体（就是我们常说的结构仿真）的主要区别。农夫山泉有一句著名的广告词叫“我们不生产水，我们是大自然的搬运工”也是很形象的说明了流体力学中连续性方程的含义：对于一个给定的观测体（仿真区域）流体不会凭空的生成和消失，流体流入多少就会对应的流出多少；同时，流体流出观测体（仿真区域）后也不会消失，而是继续的流动，一直到无穷远的地方（或循环）。】

• 

• 建立流体力学方程：基于质量守恒、动量守恒和能量守恒的流体力学方程，建立描述流体运动的数学模型。通常采用的是Navier-Stokes方程，它描述了流体的运动、压力和速度之间的关系。

• 

• 离散化和网格生成：将流体域划分为离散的小单元，形成计算网格。离散化的目的是将连续的流体域转化为离散的控制体积或控制面元，以便在每个单元上进行数值计算。

• 数值计算和求解：利用数值方法对流体力学方程进行求解。常用的数值方法包括有限差分法、有限体积法和有限元法。通过将流体力学方程在离散网格上进行数值近似，可以得到流场的数值解。
  -

• 边界条件处理：根据流体仿真模型的边界条件，对流场的边界进行处理。常见的边界条件包括速度入口条件、压力出口条件、壁面摩擦条件等。这些条件用于确定流场边界上的流体性质和流动特性。

• 迭代求解：通过迭代计算，逐步更新流场的数值解，直到达到收敛条件。迭代过程中，根据离散网格上的数值解和边界条件，计算新的压力和速度场，并更新流场的状态。

• 后处理和结果分析：对仿真结果进行后处理和分析。包括提取感兴趣的流场参数，如流速、压力分布、湍流特性等，以及对流体行为进行可视化和动态展示。

有限元仿真是否也是不能解决很多现实问题？

有限元仿真是一种在工程领域广泛应用的数值分析方法，用于模拟和分析复杂的物理现象和工程结构的行为。尽管有限元仿真在解决很多实际问题上非常有效，但仍然存在一些情况下它可能无法完全解决问题或存在限制，包括以下几个方面：

1. 精确性和准确性：有限元仿真的精确性和准确性受多个因素影响，包括模型的假设、边界条件的设置、材料参数的准确性等。在某些情况下，由于模型简化或参数估计的误差，有限元仿真结果可能与实际情况存在一定的差异。
2. 复杂物理现象：某些复杂的物理现象可能难以准确地建模和模拟，例如多物理场耦合、非线性材料行为、动态响应等。对于这些情况，有限元仿真可能需要引入更复杂的模型和算法，增加计算复杂度和计算资源需求。
3. 大规模问题：在处理大规模问题时，有限元仿真可能面临计算资源和计算时间的限制。对于复杂结构或大系统的仿真，计算资源的需求可能超出可用的计算能力，导致仿真无法进行或耗时过长。
4. 不确定性和敏感性：有限元仿真结果可能受到参数不确定性和模型假设的影响。在存在参数变化或模型假设不准确的情况下，仿真结果的可靠性和可信度可能会受到影响。
5. 边界条件和加载条件：准确设置边界条件和加载条件对于有限元仿真的结果至关重要。在某些情况下，边界条件和加载条件的获取和定义可能存在困难，导致仿真结果的可靠性受到挑战。

尽管有限元仿真存在一些限制和挑战，但它仍然是一种强大而广泛应用的工程分析工具。在实践中，合理的模型构建、验证和校准，以及与实验结果的对比和验证，可以提高有限元仿真的准确性和可靠性。此外，与其他计算方法和实验相结合使用，可以进一步提高对复杂问题的理解和解决能力。