个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

http://t.csdnimg.cn/ZxuNL个人专栏：力扣递归算法题 http://t.csdnimg.cn/ZxuNL

                  【C++】  http://t.csdnimg.cn/c9twt

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

注意：这道题目涉及到二叉搜索树的内容 ，若有不懂的可以参考下面这篇文章 

数据结构：二叉搜索树-CSDN博客

---

验证二叉搜索树

题目链接：验证二叉搜索树

题目：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

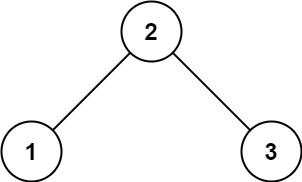
输入：root = [2,1,3]
输出：true

示例 2：

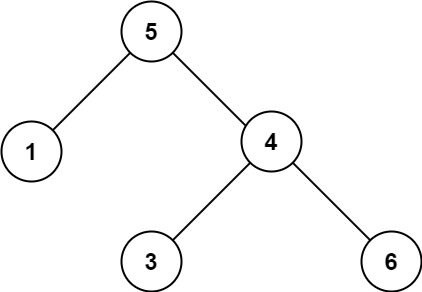
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

---

解法

题目解析

题目没什么好说的，就是给我们一颗二叉树，判断它是否为二叉搜索树

二叉搜索树有如下特性：

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

 算法原理思路讲解   

解法一：

依靠二叉搜索树的特性：中序遍历为有序

思路：创建一个全局变量 v ，中序遍历整个二叉树，然后再判断 v 是否有序即可

---

解法二：

解法一虽然也可以通过，但是我们没有必要连续插入

思路：

因此，我们可以初始化⼀个⽆穷⼩的全区变量，⽤来记录中序遍历过程中的前驱结点。那么就可以在 中序遍历的过程中，先判断是否和前驱结点构成递增序列，然后修改前驱结点为当前结点，传⼊下⼀层的递归中。

以上思路就讲解完了，大家可以先自己先做一下 

---

代码实现

解法一

• 时间复杂度：O(n)，其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，其中 n 为二叉树的节点个数。vector最多存储 n 个节点，因此需要额外的 O(n) 的空间。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> v;void dfs(TreeNode* root){if (root == nullptr){return;}dfs(root->left);v.push_back(root->val);dfs(root->right);}bool isValidBST(TreeNode* root) {bool flag = true;dfs(root);for (int i = 1; i < v.size(); i++){if (v[i-1] >= v[i]){flag = false;}}return flag;}
};

解法二

• 时间复杂度：O(n)，其中 n 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
• 空间复杂度：O(n)，其中 n 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 n ，递归最深达到 n 层，故最坏情况下空间复杂度为 O(n) 。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {long prev = LONG_MIN;
public:bool isValidBST(TreeNode* root) {if(root == nullptr) return true;bool left = isValidBST(root->left);// 剪枝（可以不用理会，若想知道，自行了解）if(left == false) return false;  // 去掉也可以通过bool cur = false;if(root->val > prev)cur = true;// 剪枝（可以不用理会，若想知道，自行了解）if(cur == false) return false;prev = root->val;bool right = isValidBST(root->right);return left && right && cur;}
};