abstract

• 除了圆和圆锥曲线外,还有许多曲线用极坐标描述会简单得多

典型曲线

• 分析下列曲线时,线分析是否含有三角函数(周期性)

• 利用描点法做出单个周期内的图形

• 作图:可以打开geogebra

  • https://www.geogebra.org/calculator/fds4duvm

  • 

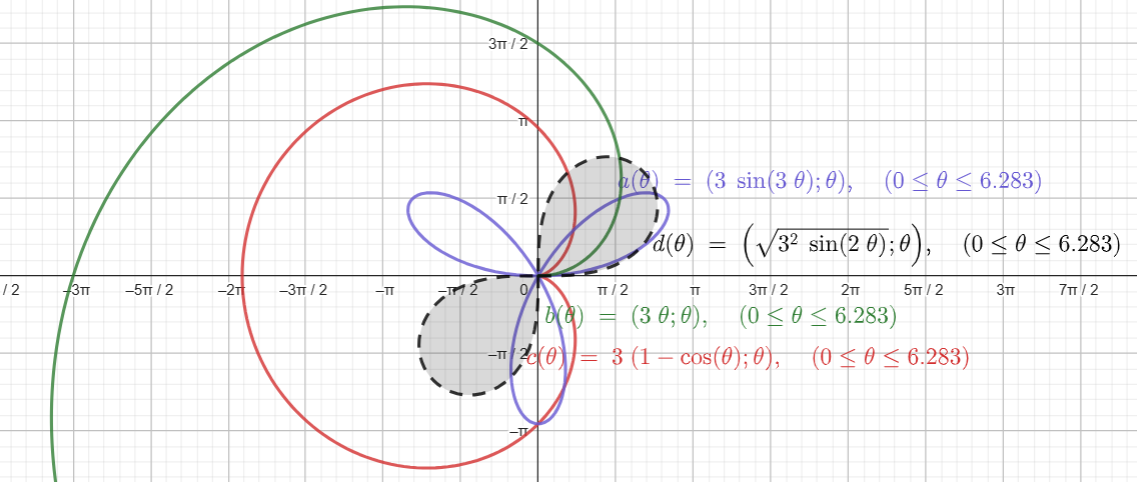
心形线

• $r$=$a(1-\cos \theta )$,$(a>0)$
  • 周期$T$=$2\pi$
  • 奇偶性:偶函数,图形关于极轴对称$(r,\theta )$,$(r,2\pi -\theta )$同时位于图形上
  • 综上,只要考虑$[0,\pi ]$上的图形,就可以通过翻折图形,的到整个周期的图形
  • 而在$[0,\pi ]$上,$\cos \theta$是从$1\to 0\to -1$的递减函数,前半程是凸函数,后半程是凹函数;
    • 从而$1-\cos \theta$从$0\to 1\to 2$是一个递增的过程,因此$a(1-\cos \theta )$从$0\to 2a$

玫瑰线

• $r$=$a\sin 3\theta$,$(a>0)$ 三叶玫瑰线

  • 周期为$T=2\pi /3$,作图时考虑$[0,\frac{2\pi }{3}]$内的区间;根据周期性,就可以直接得到$[\frac{2\pi }{3},\frac{4\pi }{3}]$以及$[\frac{4\pi }{3},2\pi ]$内的图形

  • $t=3\theta$	0	$\frac{\pi }{4}$	$\frac{\pi }{2}$	$\frac{3}{4}\pi$	$\pi$	$\frac{5}{4}\pi$	$\frac{3}{2}\pi$	$\frac{7}{4}\pi$	$2\pi$
    $\theta$	$0$	$\frac{1}{12}\pi$	$\frac{\pi }{6}$	$\frac{1}{4}\pi$	$\frac{1}{3}\pi$	$\frac{5}{12}\pi$	$\frac{1}{2}\pi$	$\frac{7}{12}\pi$	$\frac{2}{3}\pi$
    $r$=$a\sin 3\theta$	$0$	$\frac{\sqrt{2}}{2}a$	$a$	$\frac{\sqrt{2}}{2}a$	0	$-\frac{\sqrt{2}}{2}a$	$-a$	$-\frac{\sqrt{2}}{2}a$	$0$

  • 通过描点可以发现,该图形在$[0,\frac{2}{3}\pi ]$内会产生2片叶子;若将其放直角坐标系上,极点和极轴正方向分别和直角坐标系重合,则第一片叶子落在区间$[0,\frac{\pi }{3}]$;第二片叶子落在$[\frac{4}{3}\pi ,\frac{5}{3}\pi ]$;每片叶子占据$\frac{1}{3}\pi$的弧度,从顺时针的角度看,两片叶子相距$\frac{4}{3}\pi$,从顺时针看,两片叶子相距$2\pi -\frac{4}{3}\pi =\frac{2\pi }{3}$

阿基米德螺线

• $r=a\theta$,$(a>0,\theta ⩾0)$
  • 这个曲线的极坐标方程形式很简单,一个常系数$a$和极角$\theta$的乘积
  • $r$随着$\theta$的增大而增大

伯努利双扭线

• 有两种常见形式:

  1. $r^2$=$a^2\cos 2\theta$,$(a>0)$
  2. $r^2$=$a^2\sin 2\theta$,$(a>0)$

• 分析

  • 定义域:
    • 考虑到$r^2⩾0$,$a^2⩾0$,则对于形式1,2分别要求$\cos 2\theta ,\sin 2\theta ⩾0$
      • 以形式(2)为例,$\sin 2\theta ⩾0$,从而$t=2\theta \in [2k\pi ,\pi +2k\pi ]$,即$\theta \in [k\pi ,\frac{\pi }{2}+k\pi ]$
      • 容易发现图形是不连续的某些$\theta$区间上没有定义
  • 周期性:$T=\pi$
  • 奇偶性:
    • 形式(1)是偶函数,图形关于极轴对称
    • 形式(2)是奇函数,图形关于极点对称
  • 两种形式的关系:$\sin (\theta +\frac{\pi }{2})$=$\cos \theta$;则$\sin (2\theta +\frac{\pi }{2})$=$\cos 2\theta$,即$\sin 2(\theta +\frac{\pi }{4})$=$\cos \theta$,
    • 这意味着将图形(2)往负角方向旋转,即顺时针旋转$\frac{\pi }{4}$,就能得到图形(1)
    • 这和直角坐标系上的图形的$f(x+a)$是$f(x)$往$x$轴负方向移动类似(“负加正减,负向移动加,正向移动间”)

• 以形式(2)为例分析

  • 考虑到周期为$\pi$,我们研究$\theta \in [0,\pi ]$内即可,又考虑到定义域,因此我们在$\theta \in [0,\frac{\pi }{2}]$上研究

  • 为了描点,将方程(2)变形为$r$=$a\sqrt{\sin 2\theta }$

  • $\theta$	$0$	$\frac{\pi }{8}$	$\frac{\pi }{4}$	$\frac{3}{8}\pi$	$\frac{1}{2}\pi$
    $t=2\theta$	$0$	$\frac{\pi }{4}$	$\frac{\pi }{2}$	$\frac{3}{4}\pi$	$\pi$
    $r$	$0$	$\sqrt{\frac{\sqrt{2}}{2}}a$	$a$	$\sqrt{\frac{\sqrt{2}}{2}}a$	$0$

  • 从单调性分析:$\sin 2\theta$在$2\theta \in [0,\pi ]$上的变化为:$[0,\frac{\pi }{2}]$递增,$[\frac{\pi }{2},\pi ]$上递减;相应的,$\theta$区间$[0,\frac{\pi }{4}]$,$[\frac{\pi }{4},\frac{\pi }{2}]$上分别递增和递减,这就是$r$的变换规律