1. 概述

	方法	适用问题	模型特点	模型类型	学习策略	损失函数	学习算法
1	感知机	二分类	分离超平面	判别模型	极小化误分点到超平面距离	误分点到超平面距离	SGD
2	KNN	多分类，回归	特征空间，样本点	判别模型	-	-	-
3	朴素贝叶斯	多分类	特征与类别的联合概率分布，条件独立假设	生成模型	极大似然估计，极大后验概率估计	对数似然损失	概率计算公式，EM算法
4	DT	多分类，回归	分类树，回归树	判别模型	正则化的极大似然估计	对数似然损失	特征选择，生成，剪枝
5	LR与最大熵模型	多分类	特征条件下类别的条件概率分布，对数线性模型	判别模型	极大似然估计，正则化的极大似然估计	逻辑斯蒂损失	改进的迭代尺度算法，梯度下降，拟牛顿法
6	SVM	二分类	分离超平面，核技巧	判别模型	极小化正则化合页损失，软间隔最大化	合页损失	序列最小最优算法SMO
7	提升方法	二分类	弱分类器的线性组合	判别模型	极小化加法模型的指数损失	指数损失	前向分布加法
8	EM算法	概率模型参数估计	含隐变量概率模型	-	极大似然估计，极大后验概率估计	对数似然损失	迭代算法
9	隐马尔可夫模型	标注	观测序列与状态序列的联合概率分布模型	生成模型	极大似然估计，极大后验概率估计	对数似然损失	概率计算公式，EM算法
10	条件随机场	标注	状态序列条件下观测序列的条件概率分布，对数线性模型	判别模型	极大似然估计，正则化极大似然估计	对数似然损失	改进的迭代尺度算法，GD，拟牛顿法

2. 适用问题

1. 分类问题是从实例的特征向量到类标记的预测问题；
2. 标注问题是从观测序列到标记序列(或状态序列)的预测问题，可以认为分类问题是标注问题的特殊情况；

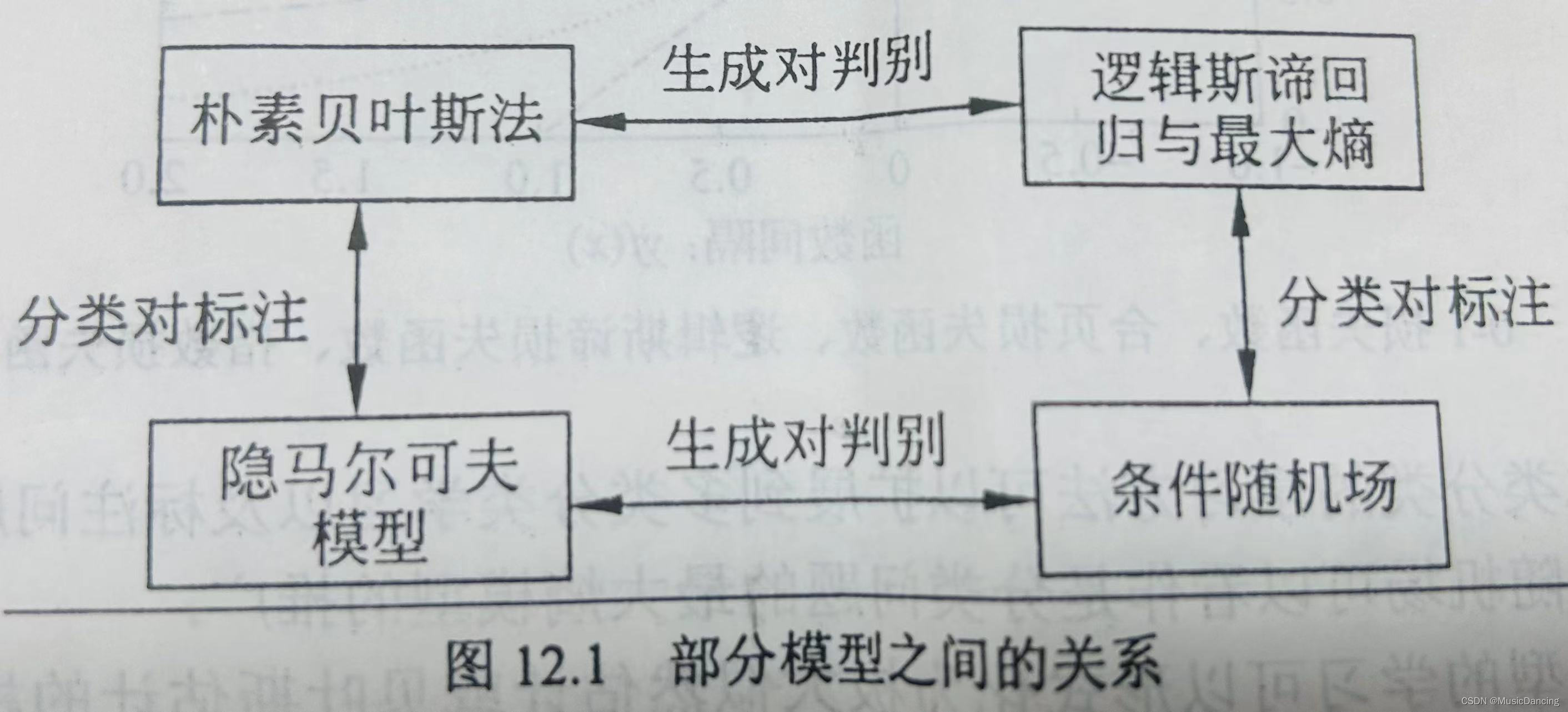
        分类问题与标注问题都可以写成条件概率分布P(Y|X)或决策函数Y=f(X)的形式，前者表示给定输入条件下输出的概率模型，后者表示输入到输出的非概率模型。有时模型更直接地表示为概率模型(如朴素贝叶斯、隐马尔可夫)，或非概率模型(如感知机，knn，SVM，提升方法)，有时模型兼有两种解释(如DT，LR与最大熵模型，条件随机场)。

3. 模型

        直接学习条件概率分布P(Y|X)或决策函数Y=f(X)的方法为判别方法，对应的模型是判别模型，如感知机，knn，DT，LR与最大熵模型，SVM，提升方法，条件随机场。

        首先学习联合概率分布P(Y|X)，从而求得条件概率分布P(Y|X)的方法是生成方法，对应的
模型是生成模型，如朴素贝叶斯、隐马尔可夫。可以用非监督学习的方法学习生成模型，朴素贝叶斯、隐马尔可夫可应用EM算法学习。

DT是定义在一般的特征空间上的，可以含有连续变量或离散变量；
感知机、svm、knn的特征空间是欧氏空间。

        感知机模型是线性模型，而LR与最大熵模型、条件随机场是对数线性模型； knn、DT、SVM(包含核函数)、提升方法使用的是非线性模型。

       

4. 学习策略

        概率模型的学习可以形式化为极大似然估计或贝叶斯估计的极大后验概率估计。这时，学习的策略是极小化对数似然损失或极小化正则化的对数似然损失 -logP(y|x) 。极大后验概率估计时，正则化项是先验概率的负对数。

         统计学习的问题有了具体的形式后，就变成了最优化问题，最优化问题大多数时候没有解析解，需要用数值计算的方法或启发式的方法求解。SVM、LR与最大熵模型、条件随机场是凸优化问题，存在全局最优解；而其他学习问题则不是凸优化问题，不能保证全局最优解存在。