题目描述
给定长度为 n 的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。
请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。
为了保证输出的二叉树中序遍历结果统一,增加以下限制:
二叉树节点中,左节点权值小于右节点权值,根节点权值为左右节点权值之和。当左右节点权值相同时,左子树高度小于等于右子树高度。
注意:
所有用例保证有效,并能生成哈夫曼树。
提醒:
哈夫曼树又称为最优二叉树,是一种带权路径长度最短的二叉树。
所谓树的带权路径长度,就是树中所有的叶节点的权值乘上其到根节点的路径长度(若根节点为 0 层,叶节点到根节点的路径长度为叶节点的层数)
输入描述
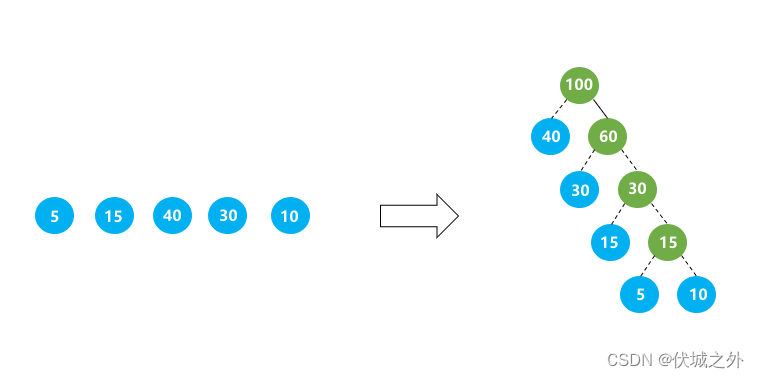
例如:由叶子节点:5 15 40 30 10,生成的最优二叉树如下图所示,该树的最短带权路径长度为:40 * 1 + 30 * 2 + 5 * 4 + 10 * 4 = 205。

:实战 Desktop、Android、iOS 调用同一个 C/C++ 代码)








)








