图形学不等于 OpenGL,不等于光线追踪,而是一套生成整个虚拟世界的方法
记得有个概念叫光栅化,就是把三维虚拟世界的事物显示在二维的屏幕上,这里就涉及到观察变换
观察变换,叫viewing transformation,包括视图变换和投影变换,投影变换又分为正交投影变换和透视投影变换
目录
视图变换
投影变换
正交投影变换
透视投影变换
视图变换
怎么理解这个视图变换呢,闫神举了个例子,比如说要拍张照片,那么把人物和场景摆放好就是模型变换,而找一个好位置放好摄像机并调好角度就是视图变换,而最后拍照成像的这个过程就是投影变换

怎么实现这个视图变换呢?我们首先来规定好摄像机的摆放参数,有一个位置,摄像机的朝向(往左往右看),还有一个向上的方向(类似于歪头)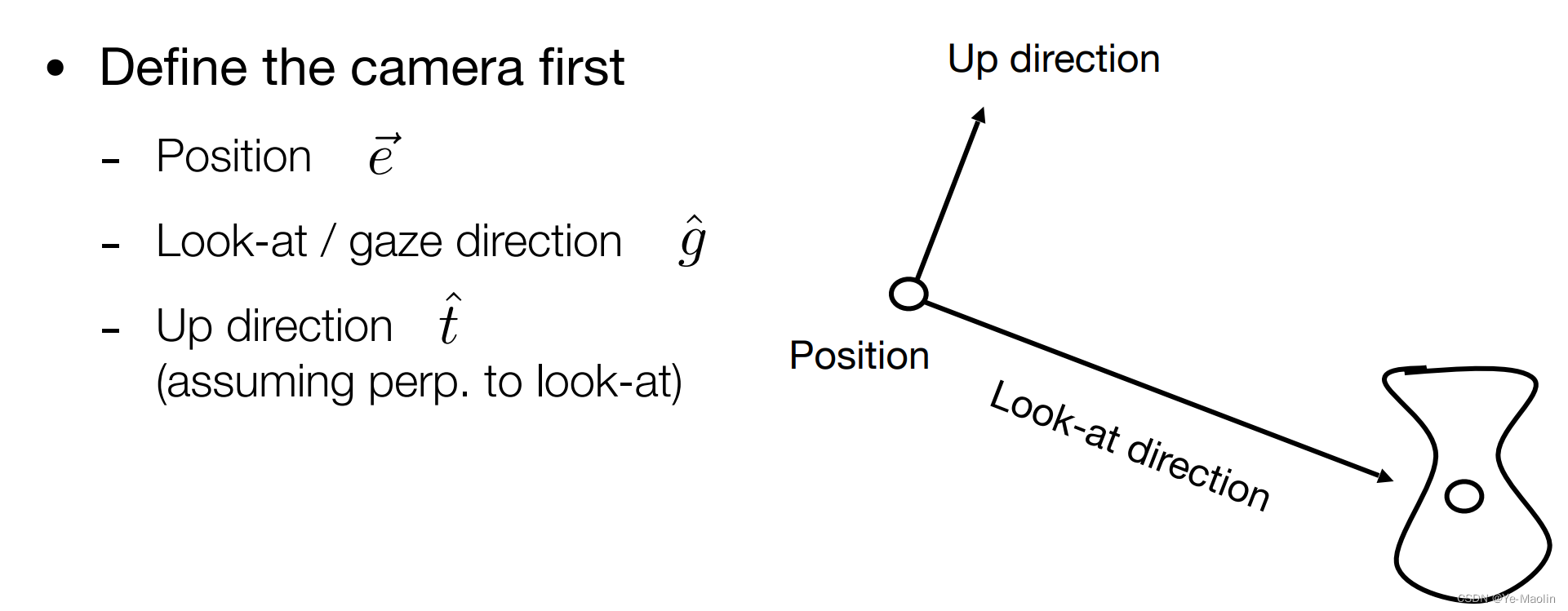
为了方便,于是约定俗成的把这个摄像机的位置放在原点处,然后让摄像机朝向z轴的负方向,向上的方向为y轴正方向
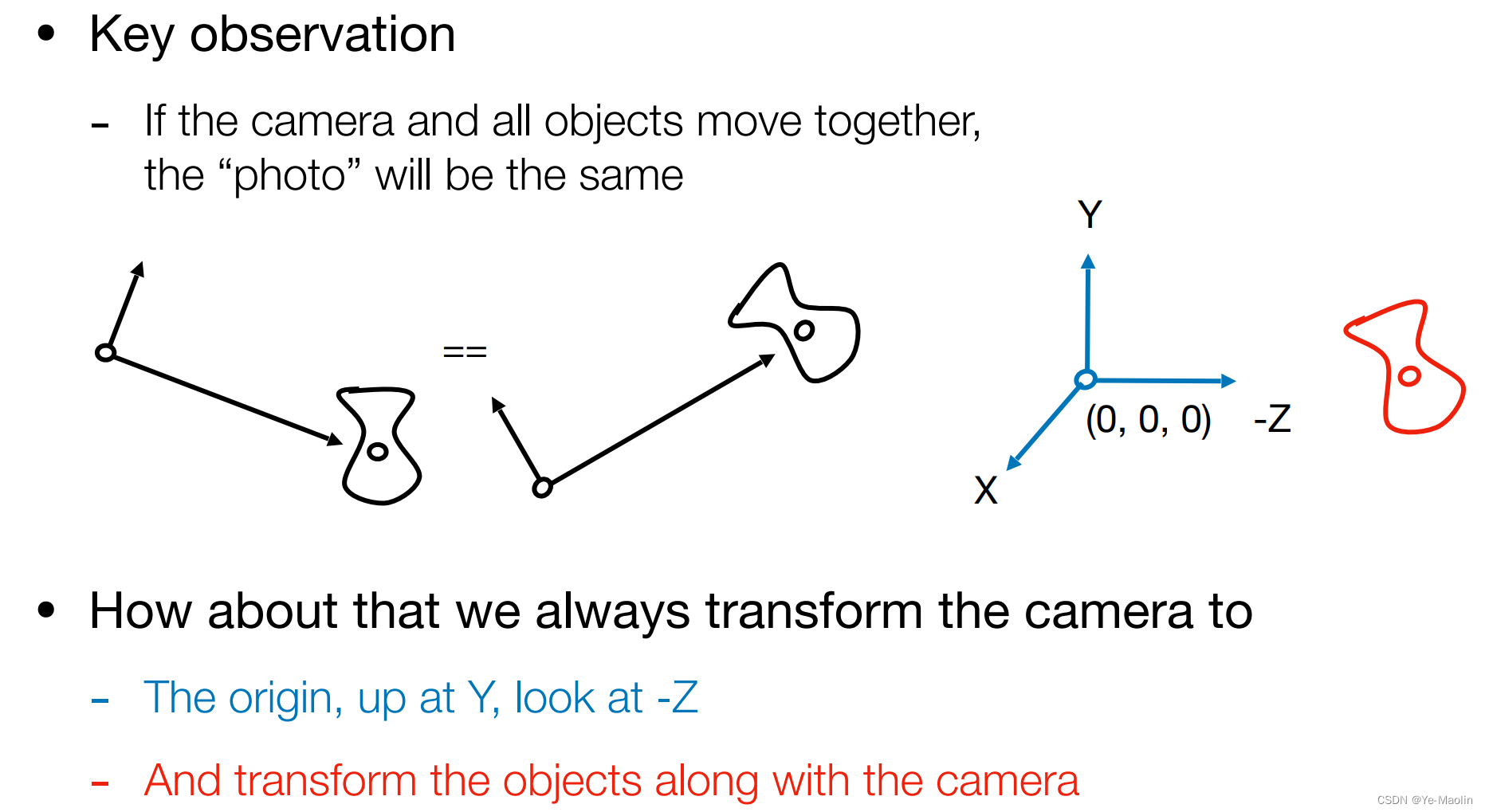
那么如何把一个摄像机移到原点并且旋转到我们需要的方向呢?
我们可以先平移在旋转,平移这个简单,直接就能写出变换矩阵来
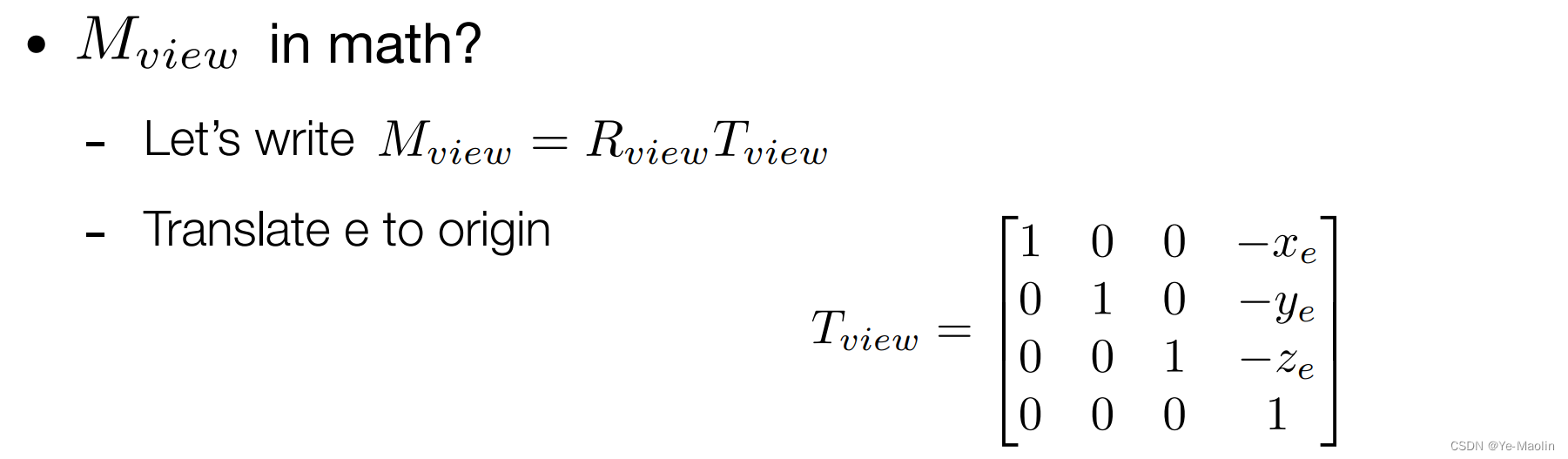
旋转呢?如果直接考虑从g旋转到-z,t旋转到y,以及g×t旋转到x,这个比较复杂,但是反过来旋转就比较简单的可以写出变换矩阵,所以我们需要的变换矩阵就是这个简单变换矩阵的逆矩阵,又因为旋转矩阵是正交矩阵,正交矩阵的逆矩阵就是其本身的转置矩阵,所以这个简单的旋转矩阵转置就是我们需要的旋转矩阵

投影变换
投影变换就是为了实现将三维的事物展示在二维上
这个透视投影呢就是近大远小,而正交投影就是相当于这个摄像机放在无限远处,那么这样近处和远处的大小看起来也是一样的了

正交投影变换
正交投影变换就是相当于把所有的点都移到XoY这个平面上,相当于这个z坐标不要了
为了显示所有的点,我们将所有的点都限制在[-1,1]里面来
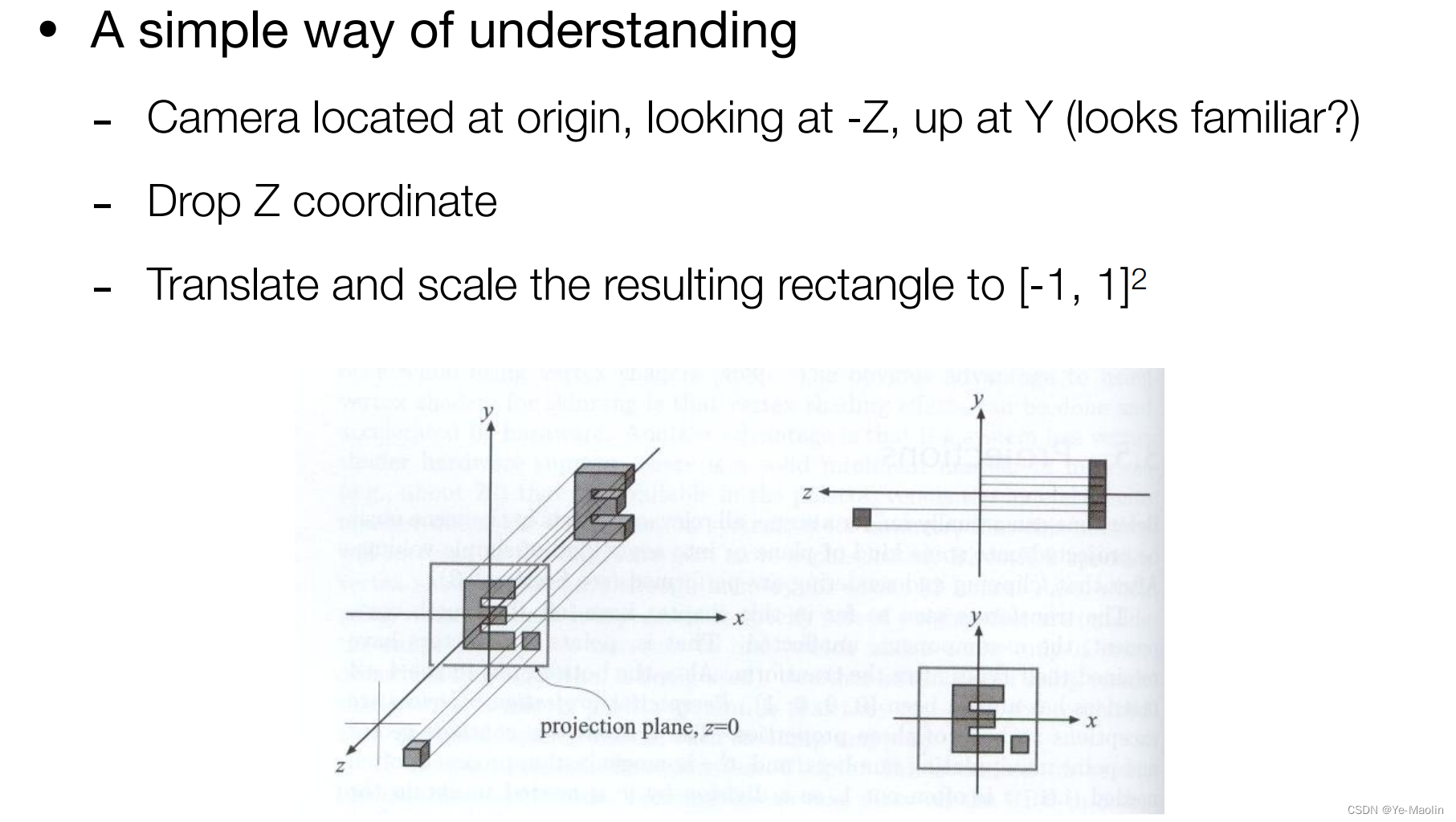
但是这样分不清远近,因此我们希望限制在一个正方体里面去,这个叫做标准的正方体,记为
[l, r] x [b, t] x [f, n]
这个l和r是left和right,就是x方向的左右,b和t呢是bottom和top,对应y方向的上下,而这个f<n是far和near,对应z方向的远近,那为什么远比近小呢?这是因为我们的摄像机是看向-z方向的
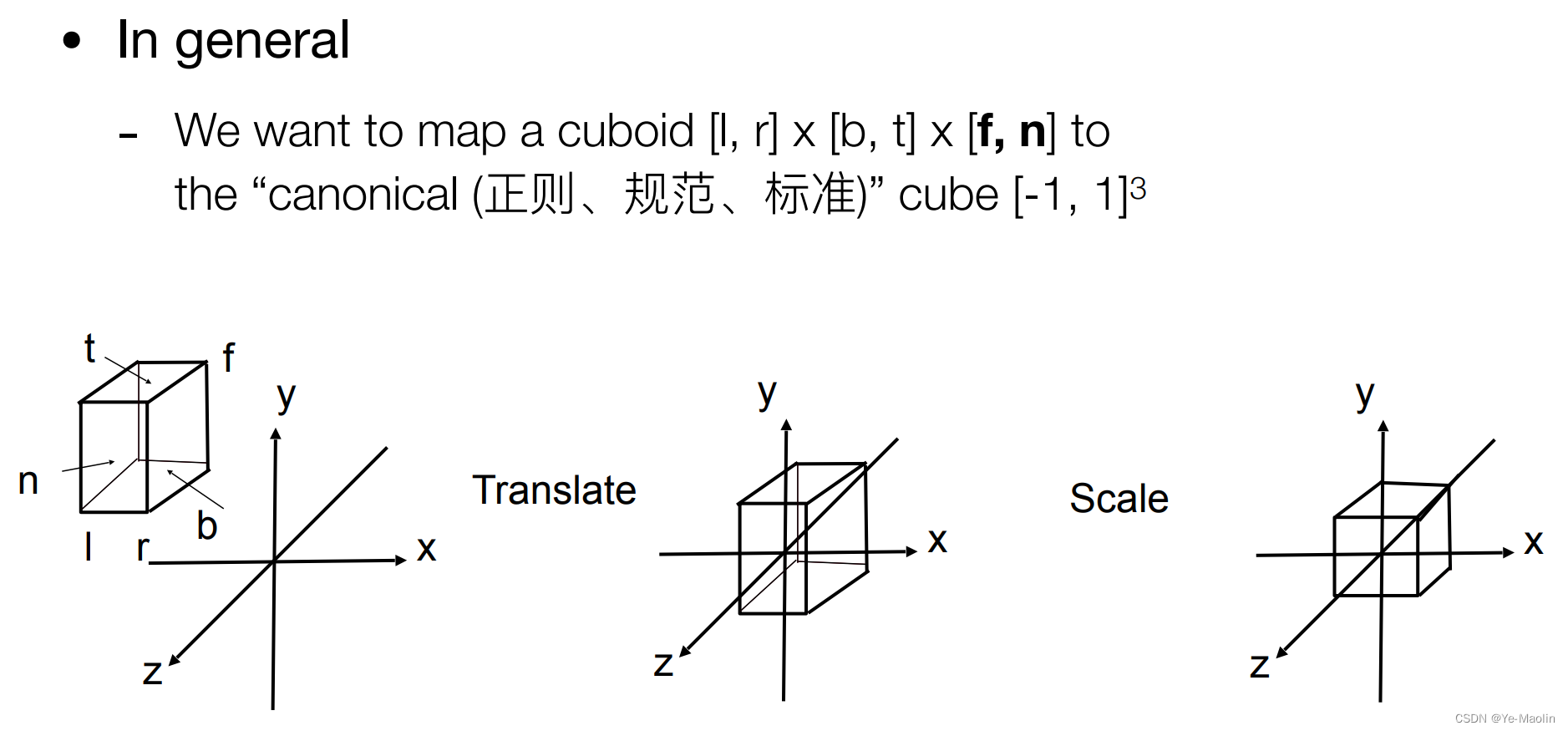
因此对于一个场景,我们通过平移和缩放两种变换就可以把它限制在这个标准的正方体里面去
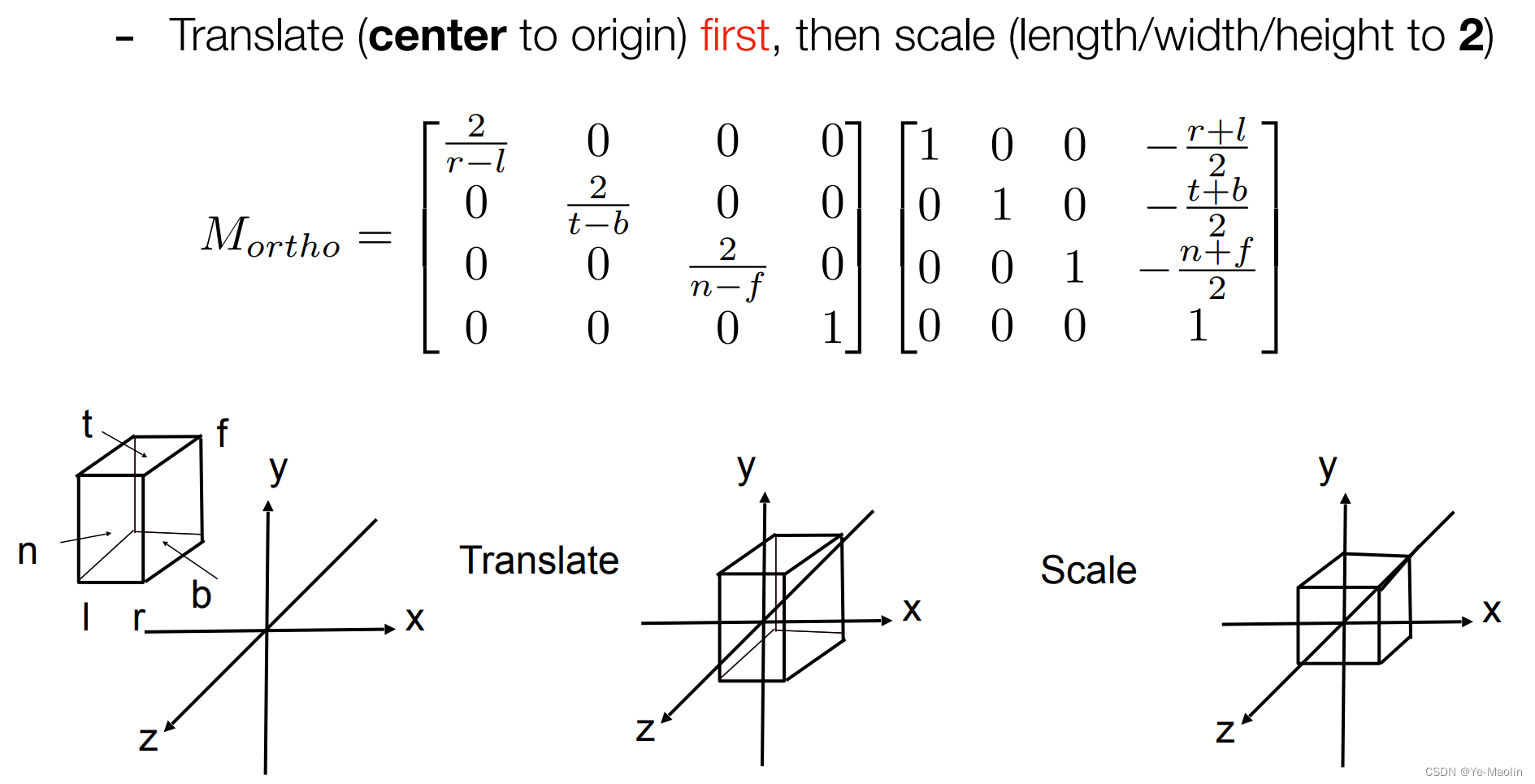
透视投影变换
透视投影比较常见,欧几里得说过,在一个平面中,永不相交的两条直线是平行线,但是透视投影却使得平行线可以看起来是相交的
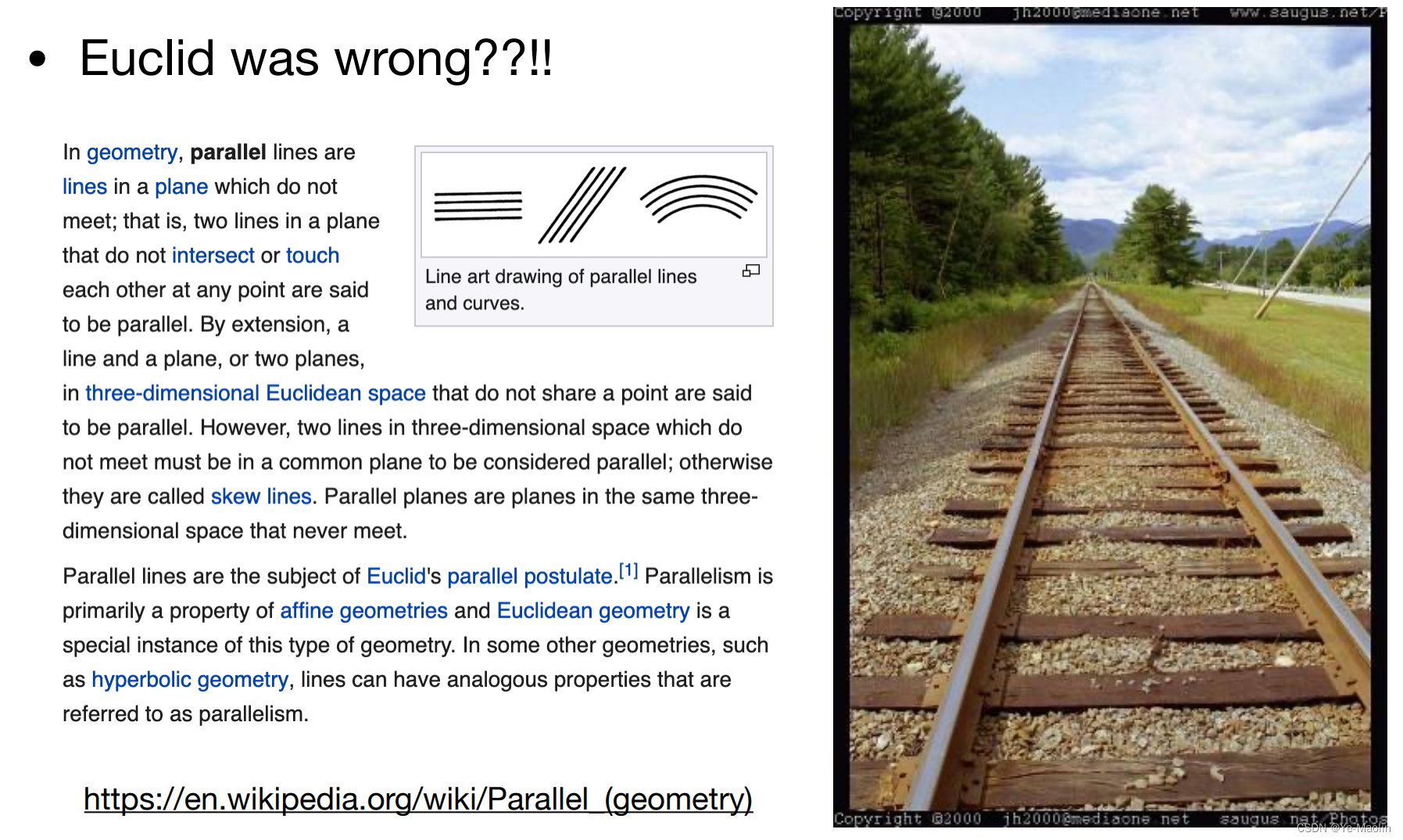
在我们开始之前,我们再回顾一下,在齐次坐标系中,对于一个点而言,如果我们直接对每个维度都乘以某个不为0的系数,那么这个点是不变的,这个点还是这个点对吧

那我们怎么来做这个投影变换呢?
实际上,我们想做的就是把这个截锥体给挤压成这个长方体,然后再做一次正交投影就行了
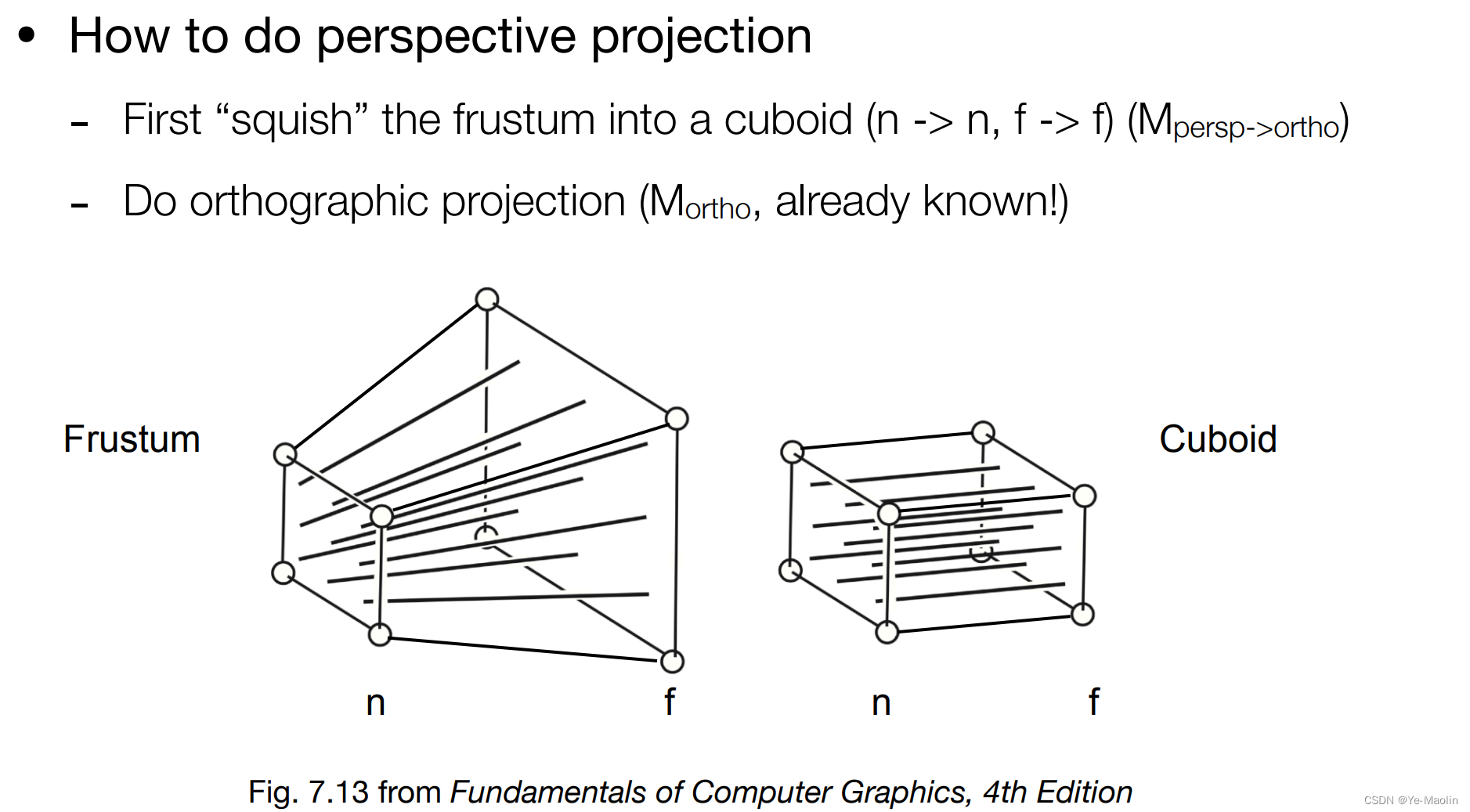
怎么挤压呢,我们可以取某个点来分析,这里用到相似三角形的原理,相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比
我们先取x和y做分析哈,那么挤压后的这个x和y就可以通过先前近平面的n和远平面的z的比值乘以x和y得到
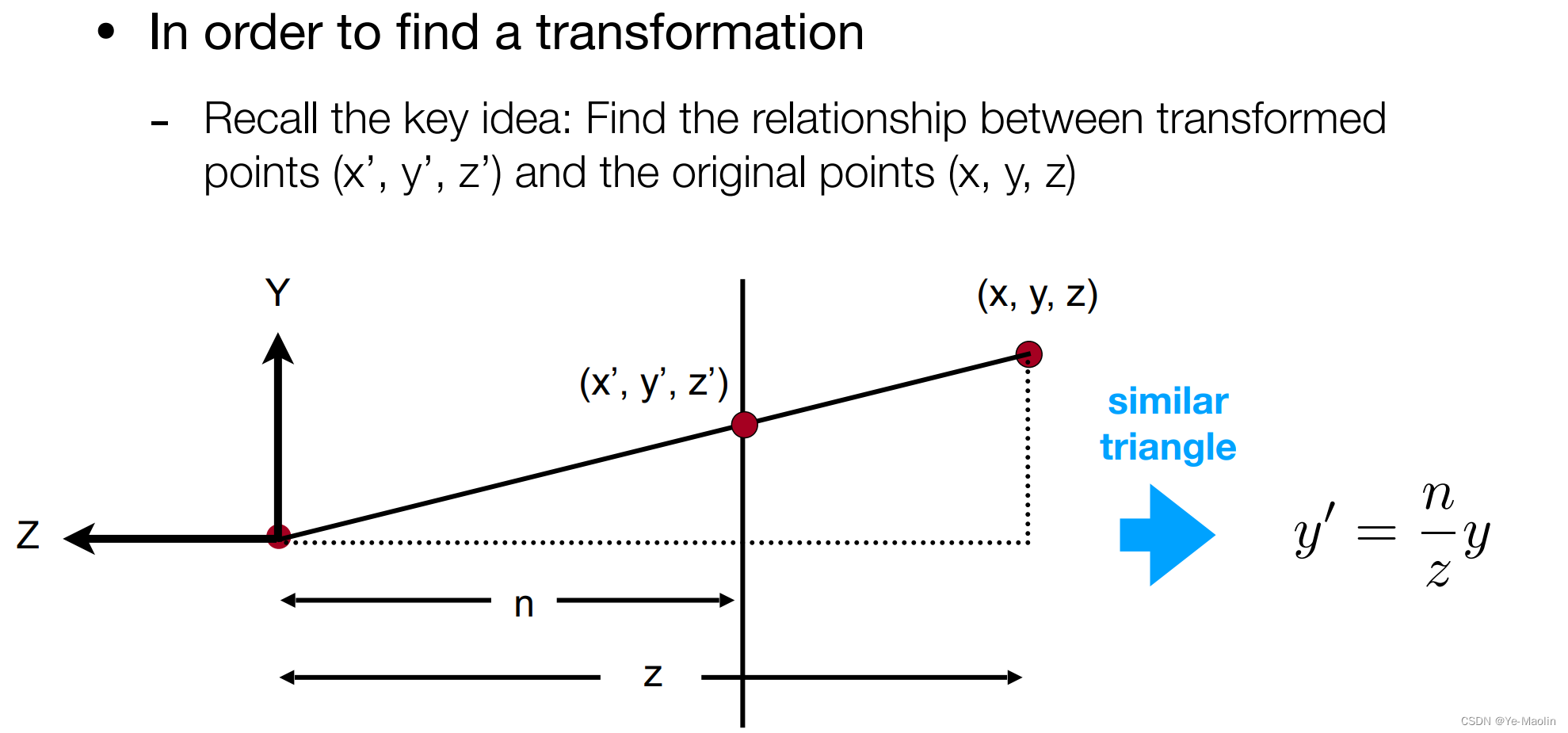
因此我们就可以找到一个这么一个对应关系使得这个点挤压过去,但是这个z会变成什么样我们还不清楚
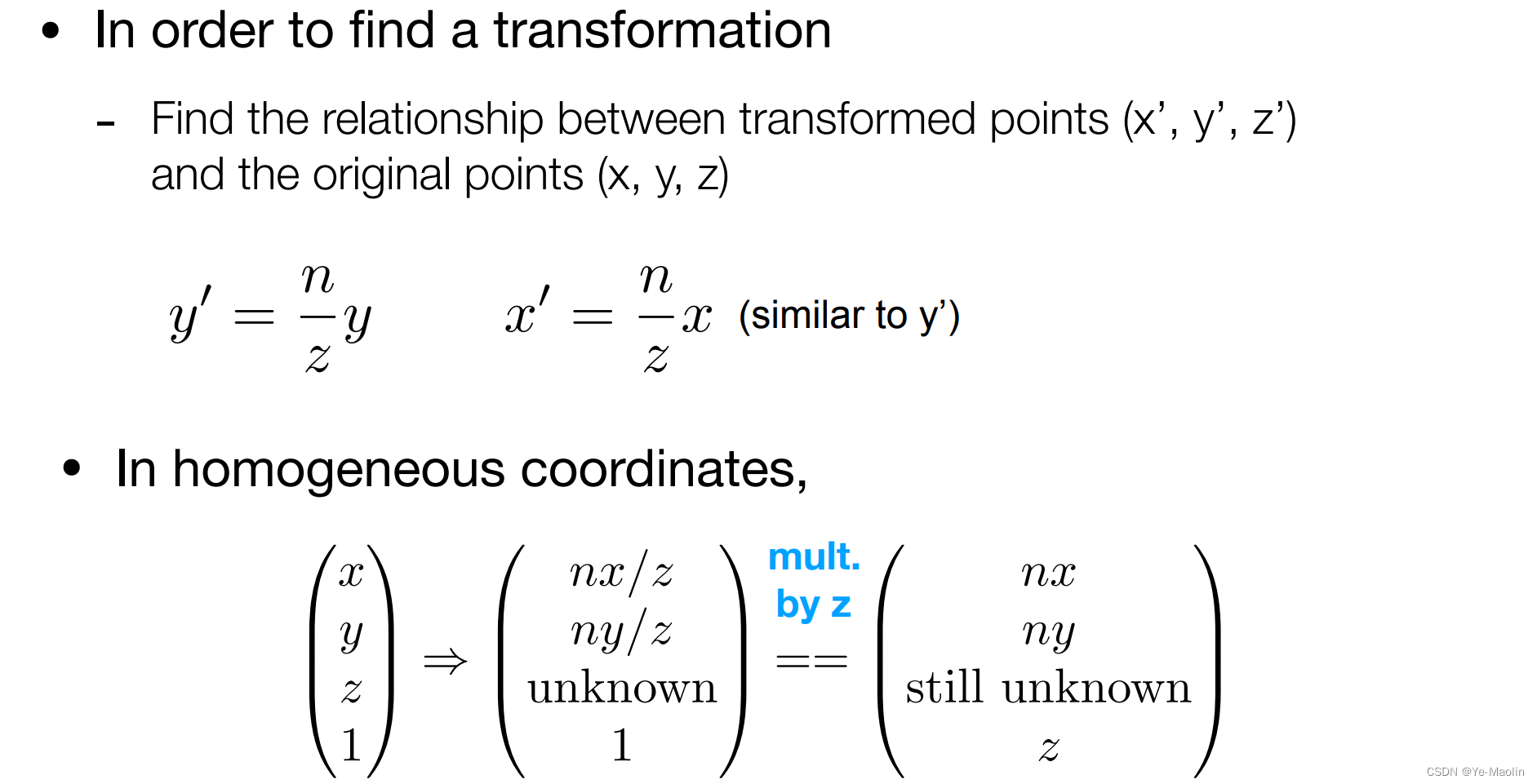
那么现在这个从透视投影变换到正交投影的变换矩阵已经有了雏形了
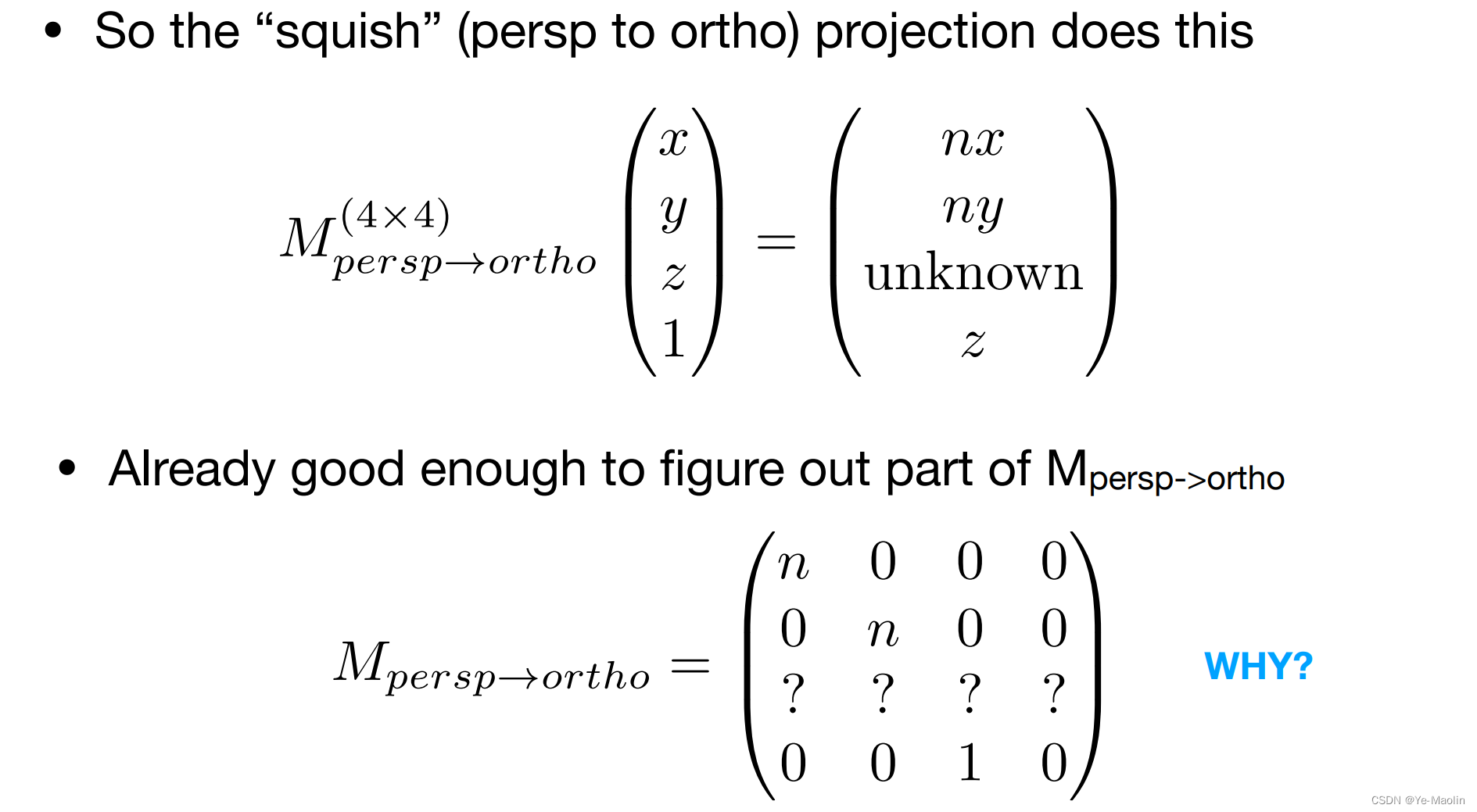
怎么解决第三行呢?
我们注意到近平面上的点在挤压后是不会发生变换的,同时远平面上的点的z坐标也不会发生变化
因此对于一个点(x,y,n,1)在挤压后应该还是(x,y,n,1),那么乘以z,也就是乘以n,这个第三行的结果应该是n²,那么这样的话,第三行应该长成(0,0,A,B)这个样,只有这样计算出来的结果才会和x和y没有关系
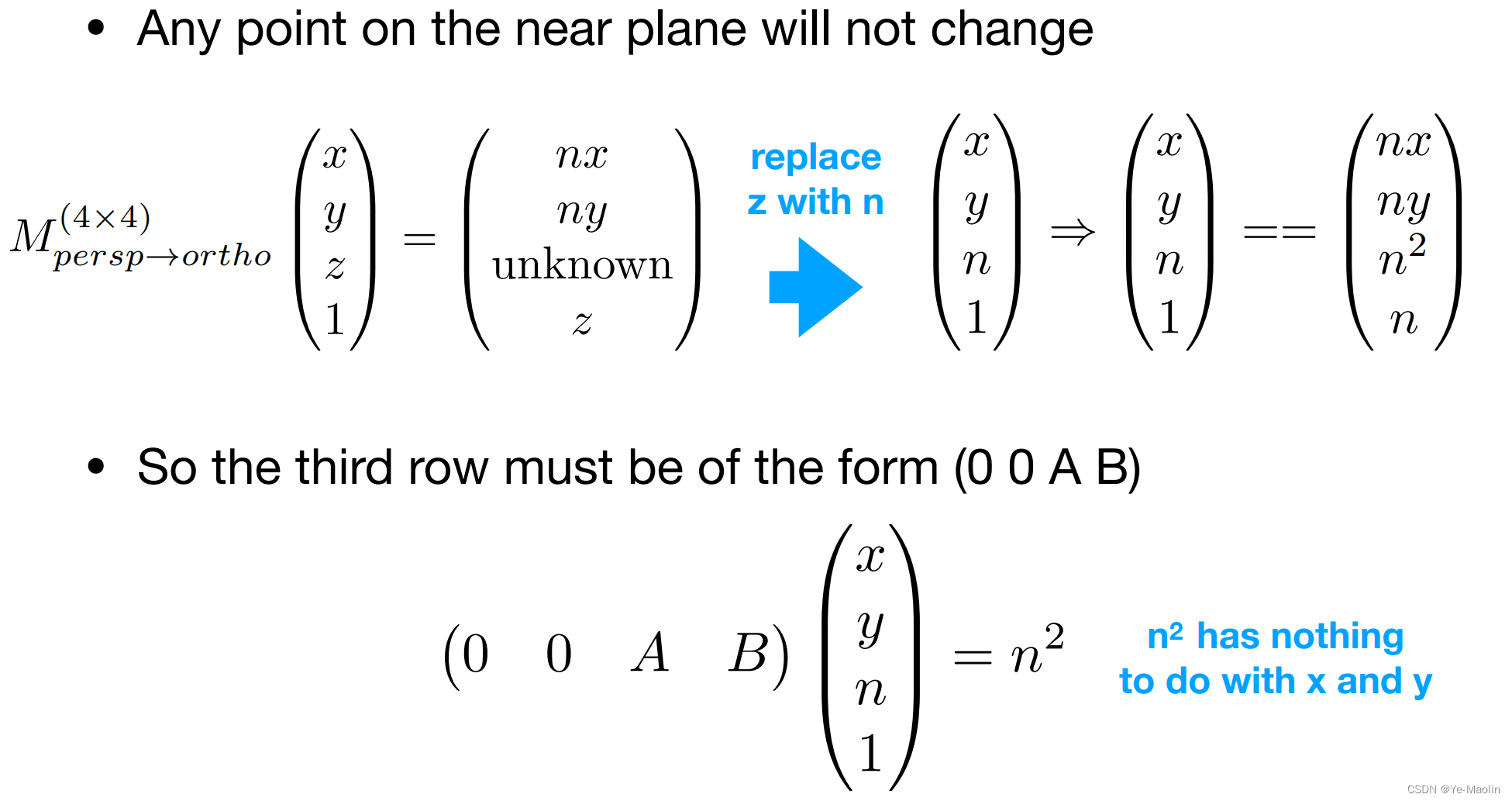
那么再加上远平面上的点挤压后z不变的结果,我们可以得到一个二元一次方程组
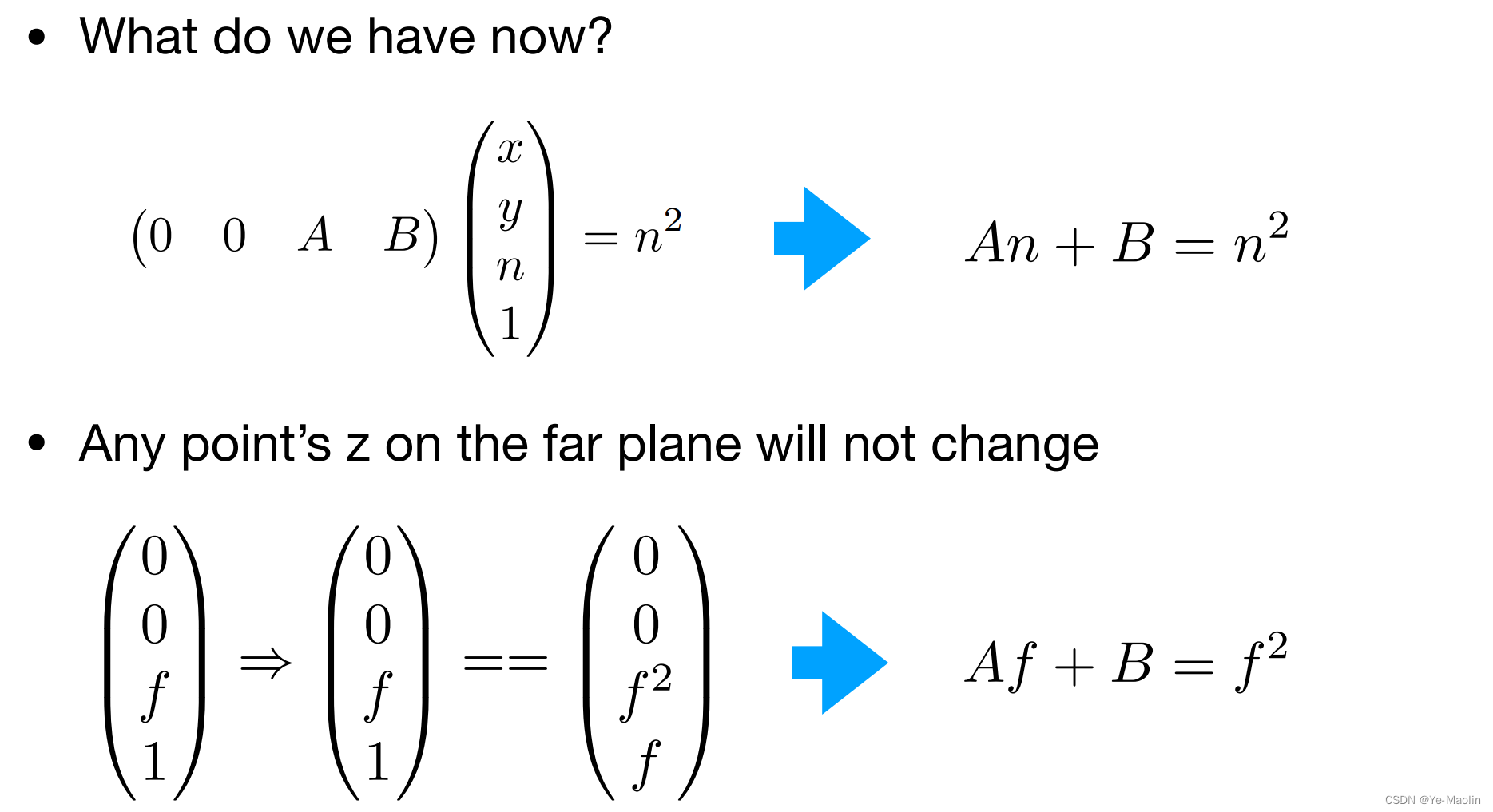
进而可以得到A和B的解,那么这个变化矩阵就找到了

这节课的最后,闫神留了个问题,在挤压的过程中,这个z坐标会如何变化,是变远呢还是变近了呢,还是不变呢





)












)
