文章目录
- 1、聚类概述
- 2、K-Means聚类算法原理
- 3、K-Means聚类实现
- 3.1 基于SKlearn实现K-Means聚类
- 3.2 自编写方式实现K-Means聚类
- 4、算法不足与解决思路
- 4.1 存在的问题
- 4.2 常见K值确定方法
- 4.3 算法评估优化思路
1、聚类概述
聚类(Clustering)是指将不同的对象划分成由多个对象组成的多个类的过程,由聚类产生的数据分组,同一组内的对象具有相似性,不同组的对象具有相异性,它是一类机器学习基础算法的总称,聚类的核心计算过程是将数据对象集合按相似程度划分成多个类,划分得到的每个类称聚类的簇。
簇(Cluster)是由距离邻近的对象组合而成的集合。聚类的最终目标是获得紧凑、独立的簇集合。一般采用相似度作为聚类的依据,两个对象的距离越近,其相似度就越大。
由于聚类时待划分的类别未知,即训练数据没有标签,因此聚类的准确率相对于分类而言较低一点,但是聚类最大的特点是可以发现新知识、新规律,因此,聚类也是了解未知世界的一种重要手段。聚类可以单独实现,通过划分寻找数据内在分布规律,也可以作其他学习任务的前驱过程。
由于聚类使用的数据是无标记的,因此聚类属于非监督学习。聚类本质上仍然是对数据类别进行划分的问题,但是由于没有固定的类别标准,因此聚类的核心问题是如何定义簇。最常用的方法是依据样本间距离、样本的空间分布密度等来确定。按照簇的定义和聚类的方式,聚类大致分为以下几种:K-Means 为代表的簇中心聚类、基于连通性的层次聚类、以EM算法为代表的概率分布聚类、以 DBSCAN 为代表的基于网格密度的聚类,以及高斯混合聚类等。
2、K-Means聚类算法原理
K-Means 聚类算法也称为K均值聚类算法,是典型的聚类算法。对于给定的数据集和需要划分的类数k,算法根据距离函数进行迭代处理,动态地把数据划分成k个簇(即类别),直到收敛为止。簇中心也称为聚类中心。
K-Means 聚类的优点是算法简单、运算速度快,即便数据集很大计算起来也较便捷。不足之处是如果数据集较大,容易获得局部最优的分类结果,而且所产生的类的大小相近,对噪声数据也比较敏感。
K-Means 算法的实现过程较为简单,首先选取k个数据点作为初始的簇中心,即聚类中心。初始的聚类中心也被称作种子。然后,逐个计算各数据点到各个聚类中心的距离,把数据点分配到离它最近的簇。一次选代之后,所有的数据点都会分配给某个簇。再根据分配结果计算出新的聚类中心,并重新计算各数据点到各种子的距离,根据距离重新进行分配。不断重复计算和重新分配的步骤,直到分配不再发生变化或满足终止条件为止。
算法的整体流程如下:
随机选择k个点作为聚类中心
while 不满足终止条件:for 数据集中的每个数据点:for k个聚类中心:计算每个点到每个聚类中心的距离比较滞后将数据点分配到最近的聚类中心for 每个簇:对聚类中心进行更新,更新为簇内所有点的均值
在上述过程中,终止条件一般可以设置为循环次数或者较小的误差值等。
由于聚类对划分的类别没有固定的定义,因此也没有固定的评价指标,一般来说聚类算法的理想目标是类内距离最小,类间的距离最大,因此,通常依此目标建立K-Means 聚类的目标函数。
假设数据集X包含n个数据点,需要划分到k个类。聚类中心用集合U表示。聚类后所有数据点到各自聚类中心的差的平方和为聚类平方和,用J表示,则J值的计算过程如下:
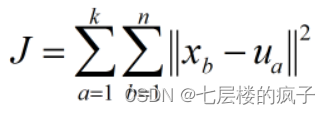
聚类的目标就是使J值最小化,如果在多次迭代之后,J值不再发生变化,说明簇的分配不再发生变化,算法已经收敛。另外计算每个点到聚类中心的距离一般采用欧氏距离进行计算。
3、K-Means聚类实现
3.1 基于SKlearn实现K-Means聚类
SKlearn的cluster模块中提供的KMeans类可以帮助实现K-means聚类,其语法格式如下:
sklearn.cluster.KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,tol=0.0001,precompute_distances='auto',verbose=0,random_state=None,copy_x=True,n_jobs=None,algorithm='auto')
在上述格式中,n_clusters表示要形成的簇的数目,即类的数量,为可选项,默认为8;init用于接收待定的string,k-means++表示该初始化策略选择的初始均值向量之间都距离比较远,它的效果较好;n_init表示用不同种子运行K-Means 算法的次数,默认为10;max_iter表示单次运行的K-Means 算法的最大迭代次数,默认300;tol表示算法收敛的阈值;precompute_distances可选参数为Boolean或auto,表示是否提前计算好样本之间的距离;verbose表示是否输出日志信息,取值为0时表示不输出,取值越大,打印次数越频繁;random_state表示随机数生成器的种子;copy_x表示在进行距离计算前,是否要将数据居中以提高计算准确性,True表示不修改数据;n_jobs表示任务使用的CPU数量;algorithm表示对K-Means经典算法的选择。
返回KMeans 対象的属性主要有:
cluster_centers_:数组类型,各个簇中心的坐标。
labels_:每个数据点的标签。
inertia_:浮点型,数据样本到它们最接近的聚类中心的距腐平方和。
n_iter_:运行的选代改数。
KMeans类主要提供三个方法,功能及语法格式分别如下:
fit方法用于进行K-means聚类计算。
fit(X[,y,sample_weight])
predict方法用于预测X中的每个样本所属的最近簇。
predict(X[,sample_weight])
fit_predict用于计算簇中心,并预测每个样本的所属簇。
fit_predict(X[,y,sample_weight])
例:对sklearn中提供的鸢尾花数据集进行聚类。
from sklearn import datasets
from sklearn.cluster import KMeans
iris = datasets.load_iris() #数据导入
X = iris.data #将特征数据作为聚类数据
y = iris.target #保留标签
clf=KMeans(n_clusters=3) #设置类别为3的聚类器
model=clf.fit(X) #训练模型
predicted=model.predict(X) #预测每个样本所属的类别
#将预测值与标签真值进行对比
print('the predicted result:\n',predicted)
print("the real answer:\n",y)

3.2 自编写方式实现K-Means聚类
除了使用SKlearn的cluster模块来实现K-Means聚类外,还可以根据实际问题采用自编写的方式来实现K-Means聚类。
例:假设某物流公司要给城市的50个客户配送货物。假设公司只有5辆货车,客户的地理坐标在testSet.txt文件中,如何进行车辆分配使得配送效率最高?
问题分析:可以使用K-Means 算法,将文件内的地址数据聚成5类,由于每类的各户地址相近,则可以分配给同一辆货车。
from numpy import *
from matplotlib import pyplot as plt
#计算两个向量的欧式距离
def distEclud(vecA, vecB):return sqrt(sum(power(vecA - vecB, 2)))
#选K个点作为初始中心点
def initCenter(dataSet, k):print('2.初始化中心点...')shape=dataSet.shapen = shape[1] #数据集列数 classCenter = array(zeros((k,n))) #数组保存中心点信息,k行n列#取数据集中前k个数据点作为初始聚类中心for j in range(n): firstK=dataSet[:k,j]classCenter[:,j] = firstKreturn classCenter#实现K-Means算法
def myKMeans(dataSet,k):m = len(dataSet) #数据集行数,即样本点个数 clusterPoints = array(zeros((m,2))) #使用clusterPoints保存数据点所属的簇序号以及距离,预设为(0,0)classCenter = initCenter(dataSet, k) #调用initCenter函数进行各簇中心初始化clusterChanged = True #用True和False表示是否要重新执行聚类的过程print('3.数据点距离计算以及簇的分配...')while clusterChanged: #重复计算,直到簇分配不再变化clusterChanged = False#将每个数据点分配到最近的簇for i in range(m): minDist = inf #首先定义一个无穷大的值作为最近距离minIndex = -1 #预设最近的簇的序号为-1for j in range(k):distJI = distEclud(classCenter[j,:],dataSet[i,:])if distJI < minDist: #如果样本点到某个簇的距离小于minDist,则将最近距离minDist以及所属簇的序号进行替换minDist = distJI; minIndex = jif clusterPoints[i,0] != minIndex: #如果第i个点所属的簇序号发生了改变clusterChanged = True #取值为True,表示要重新进行距离计算以及簇的分配,只有当所有点的簇序号不再更新时,则不在执行此过程clusterPoints[i,:] = minIndex,minDist**2 #对每个点所属的的簇序号以及距离进行更新#重新计算簇中心 for cent in range(k):#nonzero获得数据中满足条件的的元素位置下标并返回一个数组,[0]表示将数据行数单独提取出来,ptsInClust即保存了属于每个簇的数据ptsInClust = dataSet[nonzero(clusterPoints[:,0]==cent)[0]] classCenter[cent,:] = mean(ptsInClust, axis=0)return classCenter, clusterPoints
#显示聚类结果
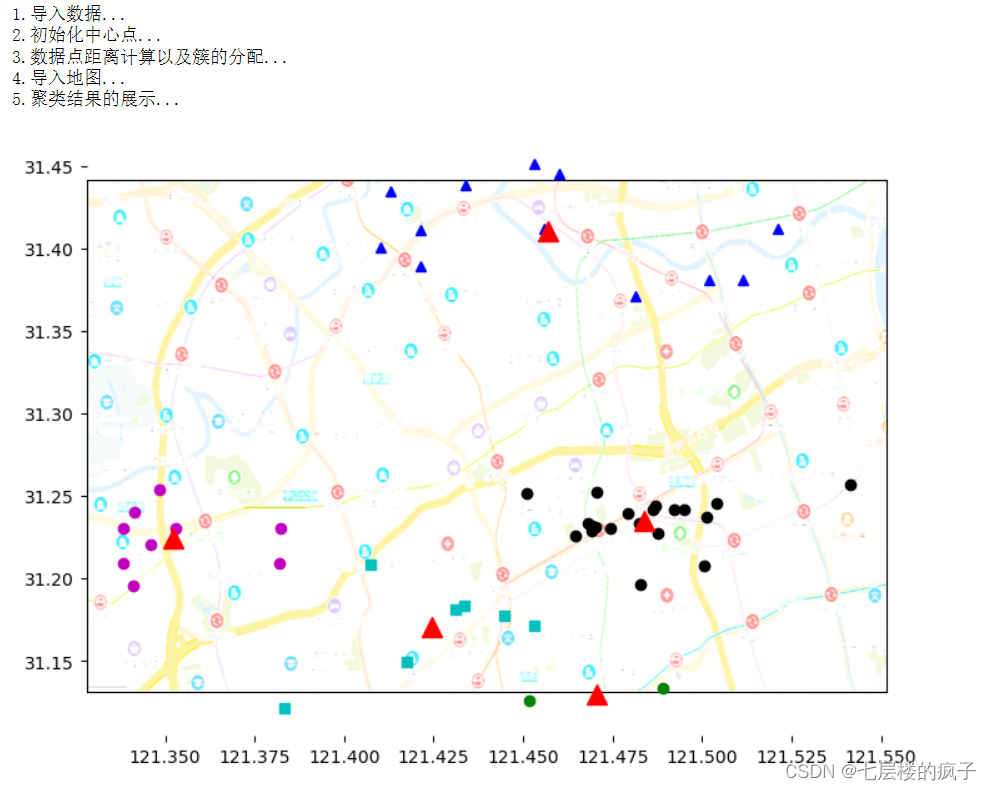
def show(dataSet, k, classCenter, clusterPoints): print('4.导入地图...')fig = plt.figure()#定义添加到图片中子区域的左下角坐标,宽度、高度rect=[0.1,0.1,1.0,1.0]axprops = dict(xticks=[], yticks=[])ax0=fig.add_axes(rect, label='ax0', **axprops) #axprops用于接收刻度值imgP = plt.imread('city.png')#在相同区域添加axes,后面添加的axes会把前面添加的axes覆盖ax0.imshow(imgP)ax1=fig.add_axes(rect, label='ax1', frameon=False) #frameon=False表示不显示边框print('5.聚类结果的展示...')numSamples = len(dataSet) #对象数量mark = ['ok', '^b', 'om', 'og', 'sc'] #根据每个对象的坐标绘制点for i in range(numSamples): #因此保存的所属簇的序号不是正整数,所以先对标签进行转换markIndex = int(clusterPoints[i, 0])%k ax1.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex]) #标记每个簇的中心点 for i in range(k): markIndex = int(clusterPoints[i, 0])%k ax1.plot(classCenter[i, 0], classCenter[i, 1], '^r', markersize = 12) plt.show()print('1.导入数据...')
dataSet=loadtxt('testSet.txt')
K=5 #类的数量
classCenter,classPoints= myKMeans(dataSet,K)
show(dataSet,K,classCenter,classPoints)
4、算法不足与解决思路
K-Means算法过程简单,实现便捷,但是该算法也存在一定的问题。
4.1 存在的问题
1、k值较难确定
大多时候并不知道数据集应该分成多少类。实际使用时,类的数量可以是经验值,也可以多次处理选取其中最优的值,或者通过类的合并或分裂得到。
2、初始聚类中心的选择对聚类结果有较大影响
例如刚刚采用自编写方式实现K-Means聚类的例子中,初始聚类中心选择的是前k个,如果将初始聚类中心修改为中间k个、后k个或者任意的k个值,所得到的结果是不同的。也就是说,初始值选择的好坏是关键性的因素,这也是K-Means 算法的一个主要问题。
3、K-Means 算法的时间开销比较大
由于算法需要重复进行计算和样本归类,又反复调整聚类中心,因此算法的时间复杂度较高。尤其当数据集比较大时,将耗费很多时间。
4、K-Means 算法的功能具有局限性
由于算法是基于距离进行分配的,当数据包含明确分开的几部分时,可以良好地划分,然而,如果数据集形状较为复杂,比如是相互存在环绕的数据集,K-Means算法就难以处理了。
4.2 常见K值确定方法
前面存在的问题主要还是存在k值的确定上,目前研究人员提出了许多确定k值的方法,常见的几种方法如下:
1、经验值
在实际问题中,大部分的样本都只会被划分成数量较少、明确的类别,因此很多时候人们会根据经验来确定k值。
2、观测值
在聚类之前,可以用绘图方法将数据集可视化,然后通过观察,人工决定将样本聚成几类。
3、肘部方法
肘部方法(Elbow Method)是将不同的模型参数与得到的结果可视化,例如拟合出折线,帮助数据分析人员选择最佳参数。
如果不同的参数对算法结果有影响,则折线图会发生变化。例如,折线图会出现拐点,类似于手臂上的“肘部”,则表示拐点位置为模型参数的关键。
4、性能指标法
通过性能指标来确定k值,例如,选取能使轮廓系数(聚类评估的方法,值越大聚类效果越好)最大的k值。
4.3 算法评估优化思路
为了进一步提高聚类效果,可以在聚类之后再进行后期处理。例如,可以对聚类结果进行评估,根据评估进行类的划分或合并。
评价聚类算法可以使用误差值,常用的评价聚类效果的指标是误差平方和SSE。SSE 的计算比较简单,统计每个点到所属的簇中心的距离的平方和。假设n代表该簇内的数据点的个数,y’表示该簇数据点的平均值,簇的误差平方和SSE 的计算公式如下:
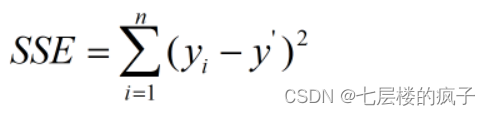
SSE值越小,表明该簇的离散程度越低,聚类效果越好。可以根据SSE值对生成的簇进行后处理,例如,将SSE值偏大的簇进行再次划分。
在K-Means算法中,由于算法收敛到局部最优,因此不同的初始值会产生不同的聚类结果。针对这个问题,使用误差值进行后处理后,离散程度高的类被拆分,得到的聚类结果更为理想。
除了在聚类之后进行处理,也可以在聚类的主过程中使用误差进行簇划分,比如常用的二分 K-Means 聚类算法。
二分K-Means 聚类的思路是首先将所有数据点看作一个簇,然后将该簇一分为二,计算每个簇内的误差指标(如SSE值),将误差最大的簇再划分成两个簇,降低聚类误差,之后不断重复进行,直到簇的个数等于用户指定的k值为止。由此思路可以看出,二分K-Means算法能够在一定程度上解决K-Means收敛于局部最优的问题。
自编写方式实现K-Means聚类物流配送问题源码及数据集




)





)








