当题目能够使用整数二分法建模时，主要有整数二分法思想进行判定，它的基本形式如下：

while(left < right)
{int ans;//记录答案 int mid = left + (right - left) / 2;//二分if(check(mid)){//检查条件，如果成立 ans = mid;//记录答案 //... 移动left或right }else{//...移动right或left	} 
}

二分法的难点在于如何建模和 check() 函数检查条件，其中可能会套用其他算法或数据结构

下面我们以洛谷P1824（进击的奶牛）为例：

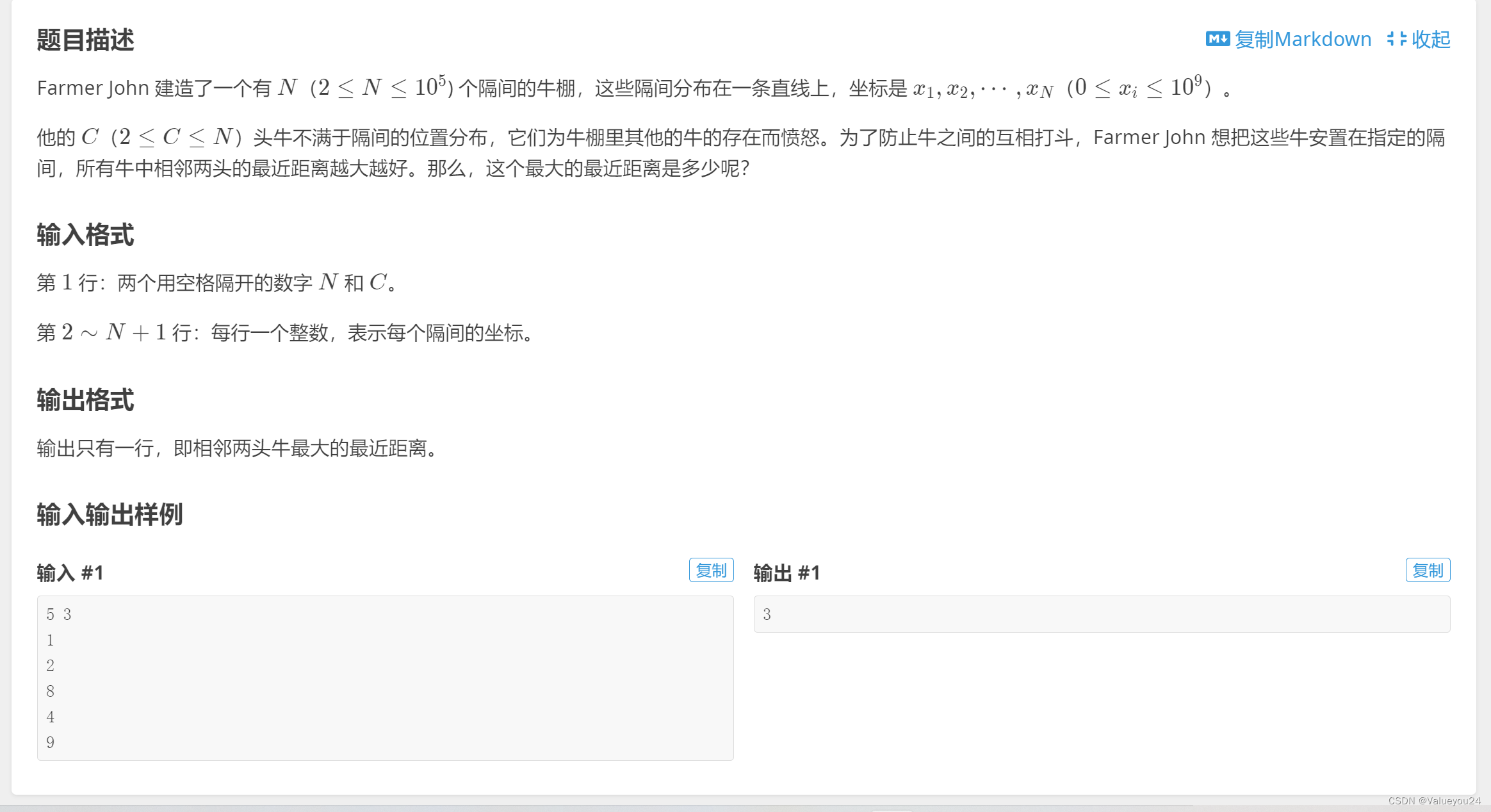
本题中，所有点两两之间的距离有一个最小值，题目要求使这个最小值最大化 

我们用二分法来实现：

#include<bits/stdc++.h>
using namespace std;int n,c;//牛棚数量、牛的数量
int x[100005];//牛棚的坐标bool check(int dis)
{int count = 1,place = 0;//第一头牛放在第一个牛棚for(int i = 1; i < n; i++){//检查后面每个牛棚 if(x[i] - x[place] >= dis){//如果距离dis的位置有牛棚 count++;//又放了一头牛 place = i;//更新上一头牛的位置	}	}if(count >= c){//牛棚够 return true;	} else{//牛棚不够 return false;}
}int main()
{cin >> n >> c;for(int i = 0; i < n; i++){cin >> x[i];}sort(x,x + n);//对坐标排序int left = 0,right = x[n - 1] - x[0];int ans = 0;while(left < right){int mid = left + (right - left) / 2;if(check(mid))//当牛棚之间的距离最小为mid时,牛棚够不够 {//牛棚够 ans = mid;//记录midleft = mid + 1;//扩大距离 }else{right = mid;//缩小距离 } }cout << ans << endl;return 0;	
}