接上回 卡通渲染总结《二》的描边技术，接下就是其绘画（The Painter）的技术。

Painter 的目的是从 3D 模型中生成平面图像。使用这种方法，可以通过改变阴影和高光参数以及着色计算的权重因子来产生各种样式。

阴影部分

单光源

首先就是人物身上的阴影部分，通常通过硬阴影，也就是存在一条固体边缘，从光照区域过渡到阴影区域。

下面的式子就是计算光照的基本式子

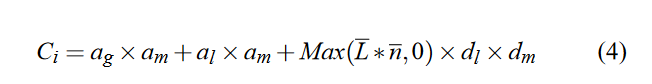
$C_i$就是顶点的颜色，$a_g$是全局环境光照系数,$a_l,d_l$分别是物体材质的环境光和漫反射系数 $\overline{L}$是光源到着色点的方向，$\overline{n}$是着色点的法线 而$\overline{L}\ast \overline{n}$表示两向量点乘，可以表示该点接收光的比例。在传统光照中其为常量，但是在卡通渲染中可以根据角度采用不同的色块。

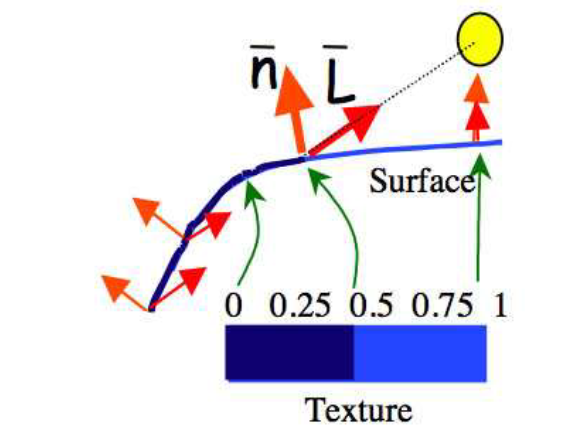
上图就表示了按照两者角度的cos值超过0.5和小于0.5划分成两种不同的颜色。并且文中提到，如果边缘出现了带有锯齿状的效果，可以使用图像API提供的纹理过滤进行处理，使得边缘更平滑，例如linear Filtering。

下图就是以这种方法的产生的阴影效果示例。

为了进一步的效率这类逐顶点的计算可以采用GPU进行加速计算。

预计算部分：

• 计算光照diffuse颜色 ：
  
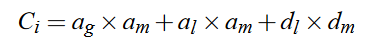
• 计算阴影diffuse颜色：
  
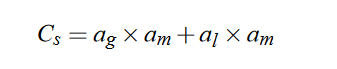
• 将两种颜色结果分别存入一维的材质中的两端

实时计算部分：

• 计算每个点的$Max(\overline{L}\ast \overline{n},0)$
• 取消光照对纹理进行采样着色

多光源

我们之前采用的都是单光源，接下去要讨论下多光源的问题。

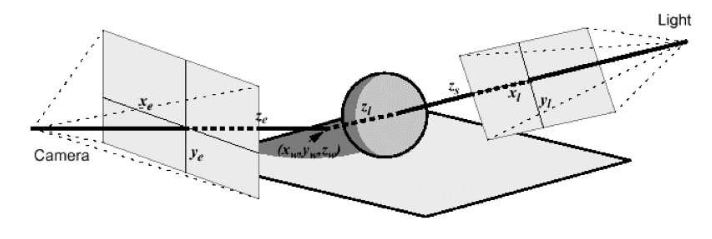
在传统shadow map的计算方法中先从光源生成一个深度图，再从视角方向检查着色点的深度和深度贴图对比，如果视角方向的着色点深度大于深度图深度就说明没收到光照。

但这个方法的z-buffer的分辨率是固定的，当相机观察物体较大，而光源观察物体较小时候，阴影会存在锯齿。

有方法提出可以平均周围像素，但其会导致阴影和光照的表面中间不再有黑色边界。因此我们可以利用之前计算的$\overline{L}\ast \overline{n}$，判断每个点属于正面或者反面进行着色，但采用这个方法需要每个光源*每个顶点计算效率不够高，所以可以将两种结合下。 对物体上的cels 着色采样本方法，对多光源产生的投射阴影采样之前的shadowmap方法。

高光参数

此外，绘画中的镜面高光通常是不是为了真实性而是为了材质效果，Winnemoller继承了先前的方法并额外实现了添加高光的效果。

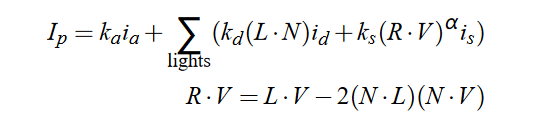
其中$R\cdot V$就是视角方向和反射方向的夹角，用于计算高光产生的程度。$\alpha$表示高光的衰减程度。

上图可以看到添加高光之后，图片变得更加的丰满创意。

我们可以对之前的一维阴影材质进行扩充到二维来计算不同的高光效果。

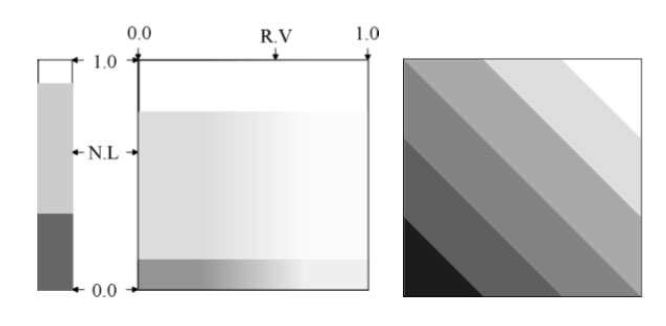
但是高光的计算是需要实时的，因为他于视角的方向有关，会带来一定的计算负担，如何去降低负担是一个重要的问题。
我们从计算复杂度去考虑，一开始，每个顶点计算一次光照，每个三角形计算两次，一次是轮廓，一次是内部着色。

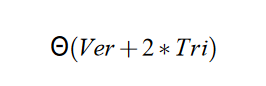
然后我们可以在三角形遍历的时候标记前后面，并减少着色的顶点百分比到b (b<1) 其实我们可以认为b接近0.5，因为大部分的面都是一正一反

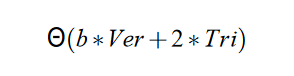
此外我们也可以在遍历顶点的过程中，标记正反面，原理就是要计算顶点的法线朝向，一个顶点的法线朝向定义为其相邻三角形法线的平均的单位向量。当然由于一个面有三个顶点，我们可以自己定义（1-3）个顶点朝前就是正面。

由于少算了一半的面复杂度就是这样了。

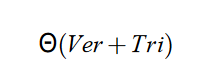
最后还有一种操作就是把视角给固定下来，当然视角在固定下来时候肯定是有问题的，但是如果你离得够远就没太大问题，因为你的视角角度的范围较小。而离得近之后就会产生洞洞。下面就是逐渐走进后的视角。

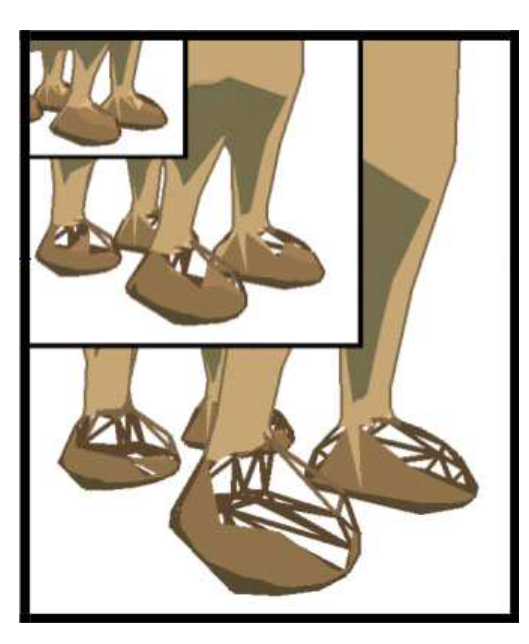
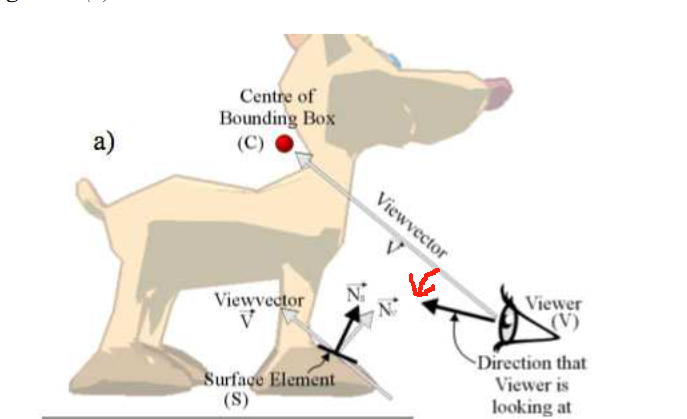
起原因就是上图所示，原本应该是正面的面被认为是反面剔除掉了没渲染出来。红色箭头表示从固定的视角到当前视角的变换。$N_s$为S点的法线，$N_v$为固定视角的法线。很明显固定视角中其cos值小于0，而当前视角确大于0 了。

当然这种固定视角也有其解决的方案，但总感觉不是很实用。

引用文献

WINNEMOLLER, H. 2002. Geometric approximations towards free specular comic shading. Computer Graphics Forum 21, 309316(8).