
🔥博客主页: 小羊失眠啦.
🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》
❤️感谢大家点赞👍收藏⭐评论✍️

文章目录
- 一、排序的概念及其运用
- 1.1 排序的概念
- 1.2 常见的算法排序
- 二、 冒泡排序
- 三、直接插入排序
- 四、希尔排序
- 五、 选择排序
- 六、各大排序算法的复杂度和稳定性
一、排序的概念及其运用
1.1 排序的概念
排序:所谓排序就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
1.2 常见的算法排序
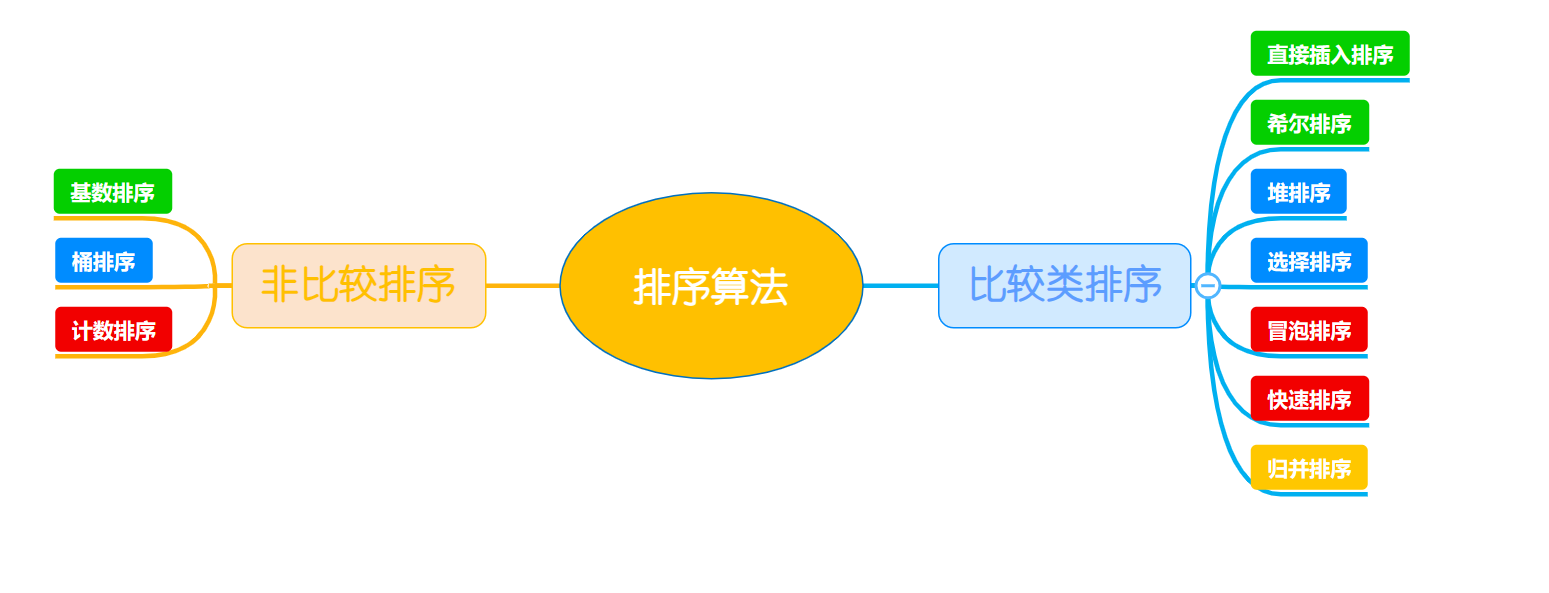
排序算法分为比较类排序和非比较类排序,如下图所示:
二、 冒泡排序
- 思想 : 在一个序列中,每次对序列中的相邻记录的键值大小进行比较,将
较大(升序)或较小(降序)的记录向后移动。如此循环,大/小的记录会慢慢“浮”到序列的后端,整个过程就像是冒泡一样,顾称之为冒泡排序。 - **冒泡过程:**以下是对某个序列进行冒泡排序的过程
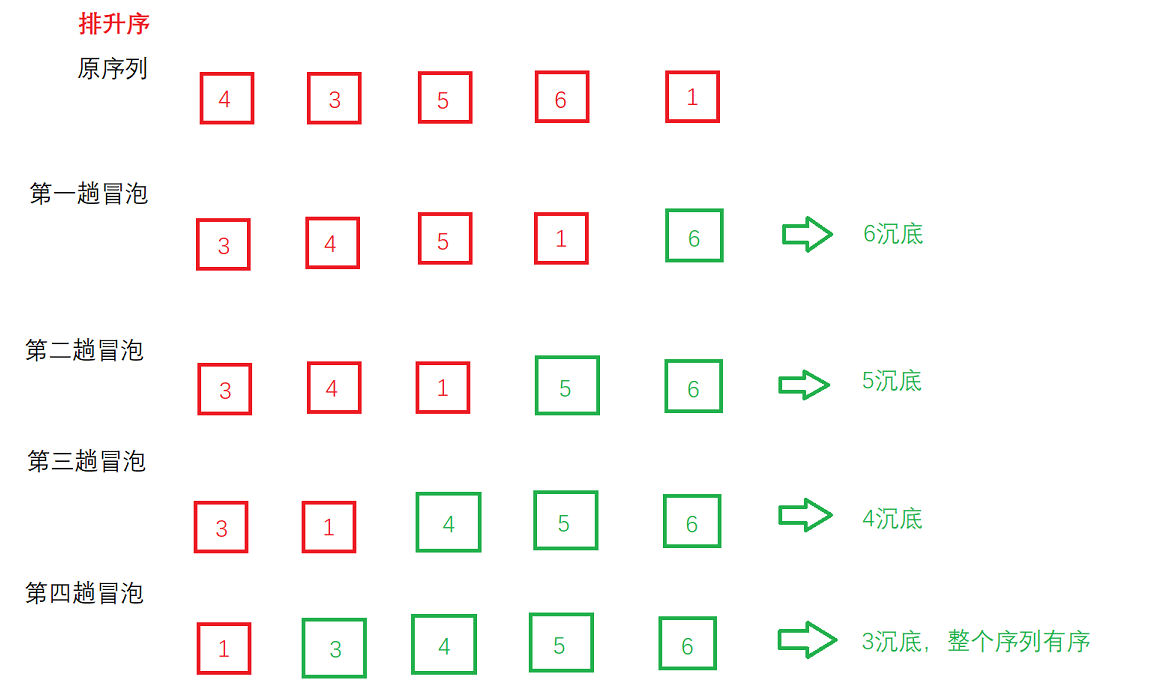
可以看出,对于上面具有5个元素的无序数组,我们通过4趟的冒泡后就将其变为有序数组,每一趟冒泡后都可以使最大的数沉底。
- **动图演示:**我们可以通过一下动图感受一下冒泡两两比较的过程:
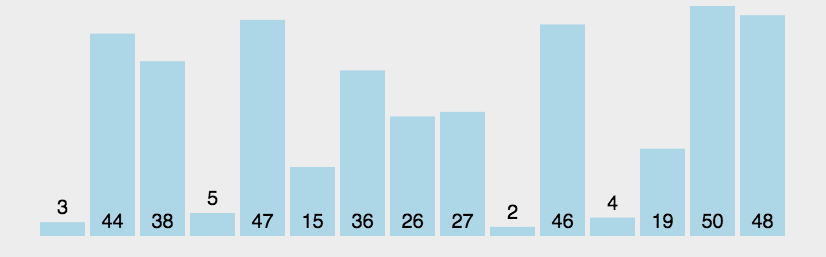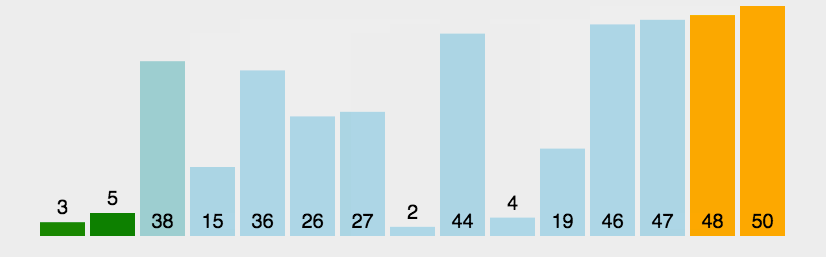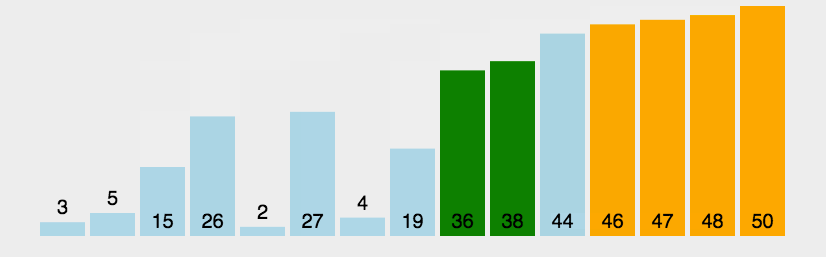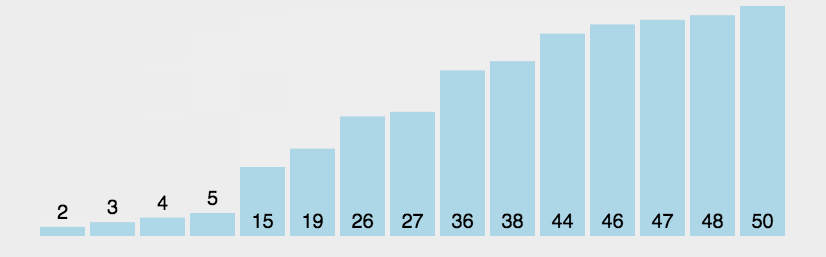
- **循环控制:**很明显,我们需要两层循环来控制冒泡排序的过程。
内层循环控制当前趟的数据交换,外层循环控制冒泡排序的趟数。 - **外层循环结束条件:**由于每一趟结束后都有一个数冒到序列后端,因此对于N个数的序列来说,一共需要N-1趟(只剩一个数不需要冒泡)。
for (int i = 0; i < n - 1; i++) //外层循环,N-1趟
{;
}
- **内层循环结束条件:**内层循环用于数据的比较。已知N个数据共需比较N-1次,由于每一趟结束后就有数据到正确的位置,下一趟需要比较的数据个数就会少1,因此
每趟的比较次数随着趟数的增加呈递减趋势,初始为N-1次。
for (int i = 0; i < n - 1; i++) //外层循环,N-1趟
{for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{;}
}
- 完整代码:
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void BubblingSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) //外层循环,N-1趟{for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{if (a[j] > a[j + 1]) //升序排列,较大的往后移{swap(&a[j], &a[j + 1]); //交换}}}
}
- **改进优化:**上面的代码还存在着改进空间,我们来看下面两个情景:
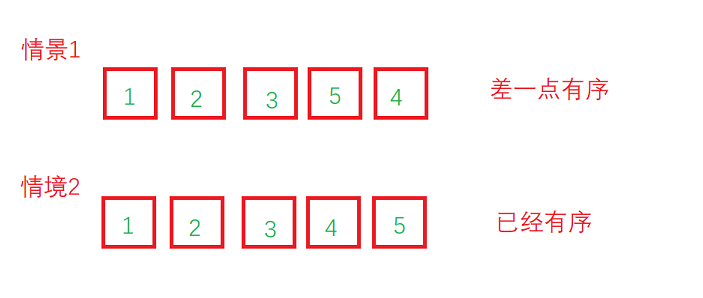
对于情境1,我们只需一趟冒泡即可让数组有序,而如果按照上面的代码,我们依旧要进行4趟的冒泡,即有三趟是无效的。
而情境2就更夸张了,数组已经有序,我们却傻乎乎的做了4趟无效冒泡。无疑是非常浪费时间的。
考虑到这些情况,我们提出了优化方案:
在每趟结束后判断一下当前趟是否发生了元素交换,如果没有,则说明序列已经有序了,及时止损,反之继续。优化后的代码如下:void swap(int* x, int* y) {int tmp = *x;*x = *y;*y = tmp; }void BubblingSort(int* a, int n) {for (int i = 0; i < n - 1; i++) //外层循环,N-1趟{int flag = 0;for (int j = 0; j < n - 1 - i; j++) //内层循环,次数随趟数增加而递减,初始为N-1{if (a[j] > a[j + 1]) //升序排列,较大的往后移{swap(&a[j], &a[j + 1]); //交换flag = 1;}}if (flag == 0)break;} }
- 时间/空间复杂度:结合上面的图片和代码我们可以看出,总共N-1趟,每趟N-1,N-2…次比较,共比较 (N-1) + (N-2) + (N-3) + (N-4) + (N-5) + … + 1次,时间复杂度为O(N^2);而由于没有额外的辅助空间,空间复杂度为O(1)。
- 稳定性分析:由于我们是将较大的或较小的进行交换,当两个数相等时并不会进行交换,因而不会改变相同元素的先后次序,所以冒泡排序是稳定的排序。
三、直接插入排序
- 基本思想
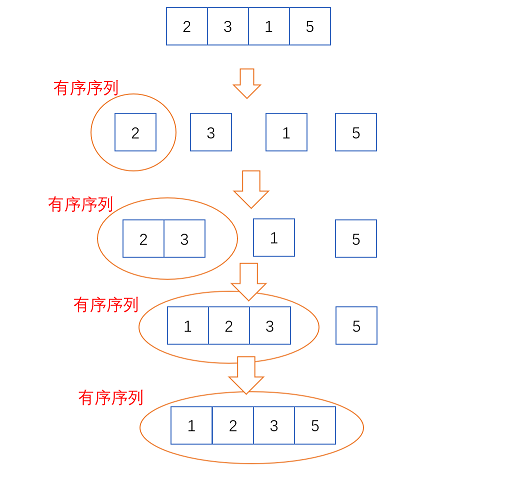
插入排序的基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
- 过程分析
我们可以将第一个元素作为一个有序序列,从第二个元素开始插入到这个有序序列中,过程如下:
以升序为例:
当插入第i个元素时(i>=1),说明前面的array[0],array[1],…,array[i-1]已经排好序,我们将array[i]位置的值从后往前与array[i-1],array[i-2],…依次进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移。
为什么不从前往后开始进行比较?
如果我们从前往后进行比较,当找到插入位置时,根据顺序表的插入我们知道:必须先将后面的元素全部后移,而后移又不能从前往后移,否则会造成元素覆盖,我们必须从后往前移动。折腾了半天又要
从后往前遍历,那为什么不一开始就从后往前比较,在比较的同时一并挪动元素,何乐而不为呢?
单趟插入动图:
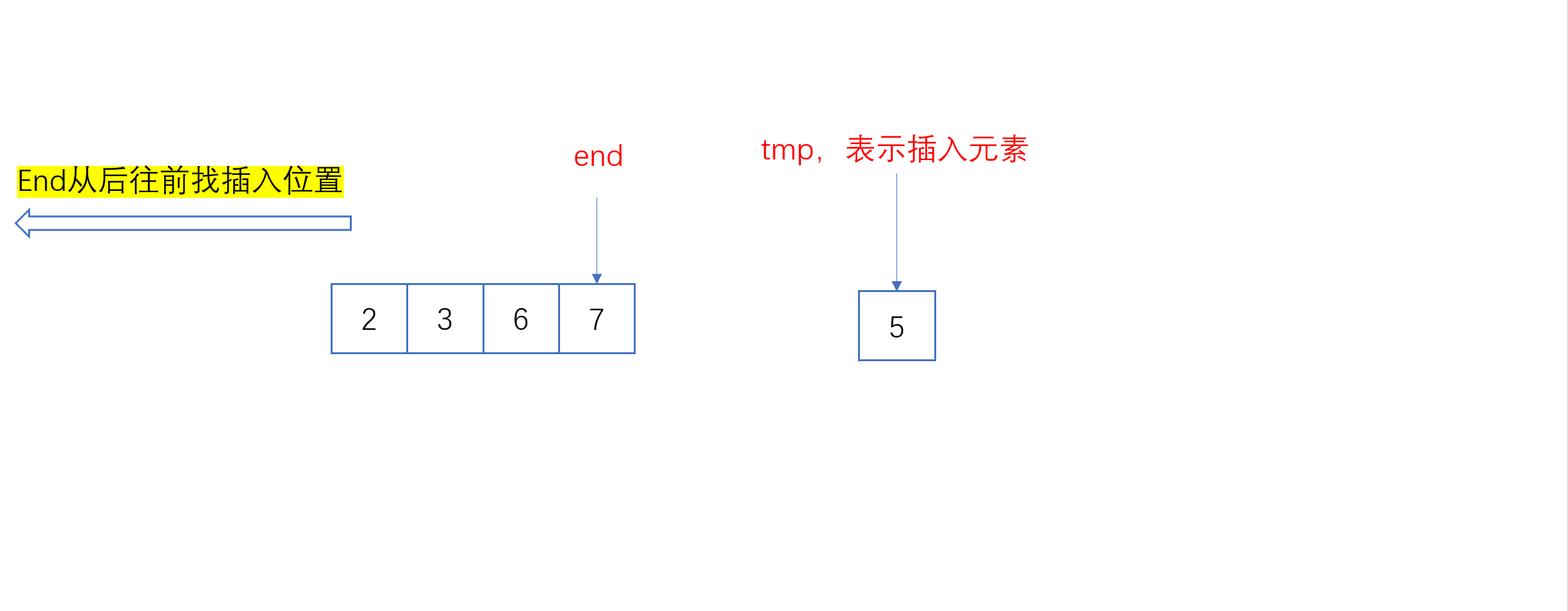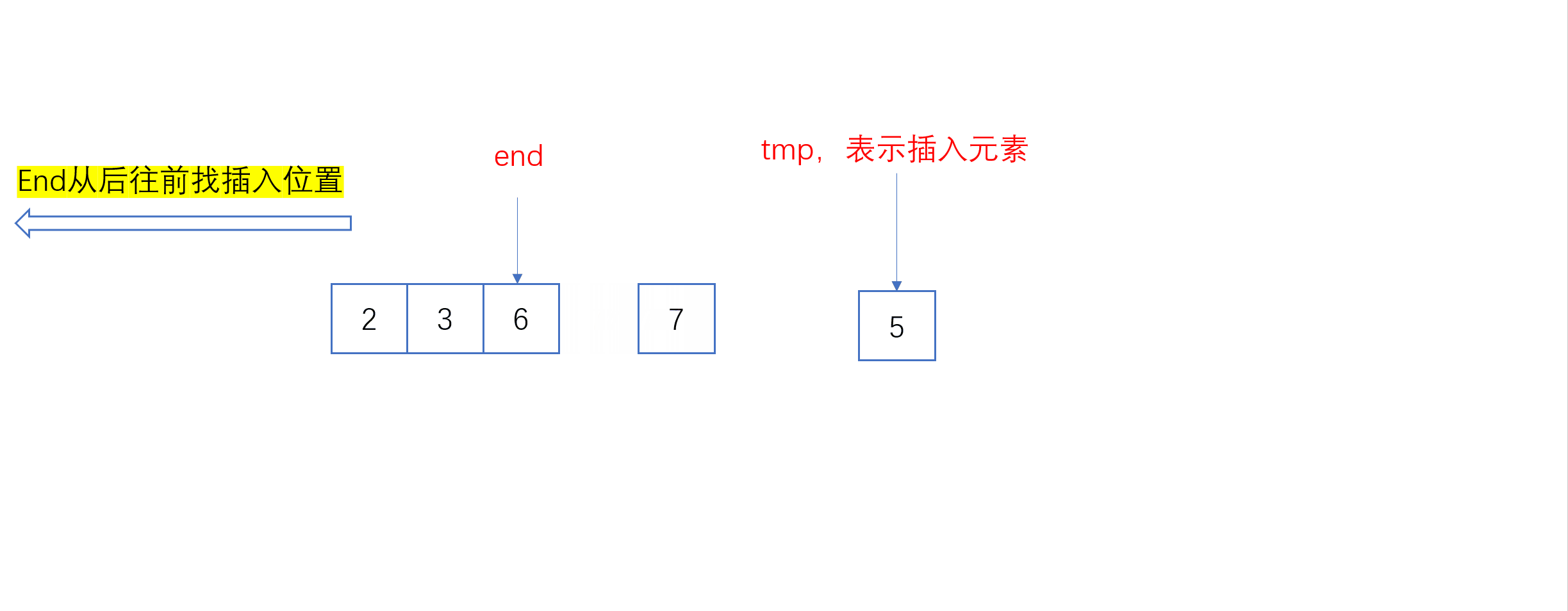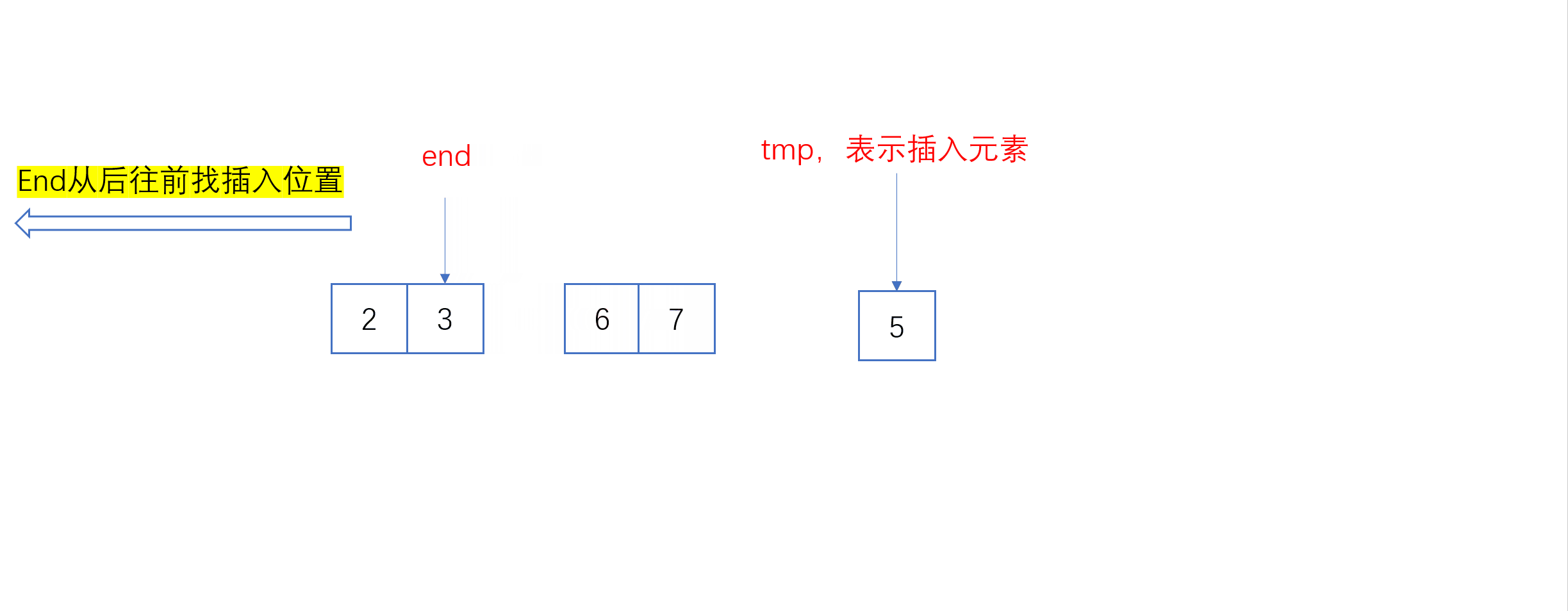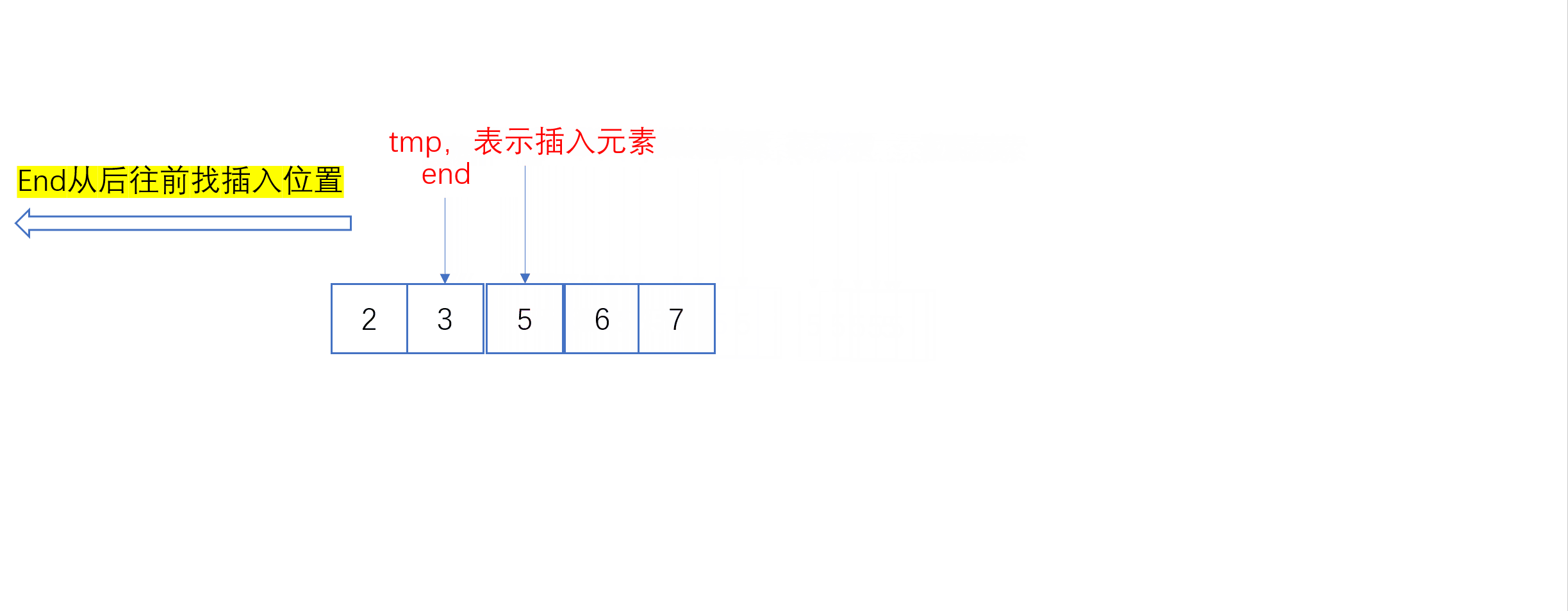
全过程动图:
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp)a[end + 1] = a[end];elsebreak;end--;}a[end + 1] = tmp;}
}
复杂度/稳定性分析
复杂度:
根据上面的动图我们可以发现,当元素集合越接近有序,直接插入的时间效率越高,当元素集合已经有序时,时间复杂度便是O(N),即遍历一遍数组(最优情况)。
而时间复杂度我们看的是最坏情况,即数组元素逆序的情况。此时每次插入相当于头插,而头插的时间复杂度为O(N),因此总时间复杂度为O( 插入次数 * 单次插入时间复杂度 ) = O(N^2)。
而除了待排序数组之外只有常数级的辅助空间,空间复杂度为O(1)。
稳定性:
由于我们是大于tmp才进行元素挪动,当等于tmp时直接将tmp放到后方,不会对相同元素的顺序进行改变,因此直接插入排序是稳定的排序
四、希尔排序
- 基本思想
希尔排序又称缩小增量法,其基本思想是:选出一个整数gap表示增量,根据gap将待排序的记录分为gap组,所有距离为gap的记录分在同一组,然后对每一组进行直接插入排序。随着排序次数的增多,增量gap逐渐减少,当gap=1时,即所有记录分在同一组进行直接插入排序,排序完成后序列便有序了,算法结束。分组方法如下:
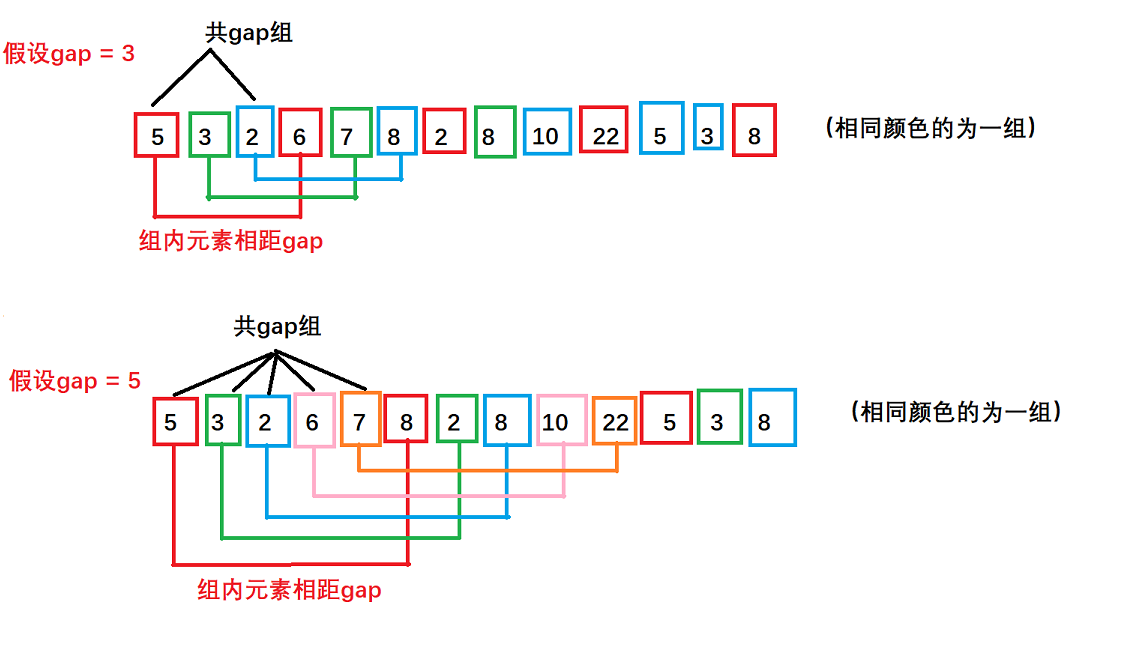

过程分析:
- 首先,我们需要对gap的初始值进行确定,这并没有一个确定的答案,一般是按照数据量来进行选取。一般我们选取gap = n/3 + 1或者gap = n/2作为gap的初始值。
- 根据算法的思想,我们观察到gap是在不断地进行缩小,最后缩小到1进行直接插入排序。因此我们gap的缩小增量可以继续使用gap = gap/3 + 1或gap = n/2来表示。
- 对1、2点进行合并后,我们可以这样用来表示gap的迭代更新:
int gap = n; //n为序列元素个数
while(gap > 1)
{//gap = gap/2;gap = gap/3 + 1;//每组进行直接插入排序//...
}
上面的循环在以下两种情况下会结束:
- n == 1:即
序列只有一个元素,此时无需进行排序,不会进入循环- n != 1 ,gap == 1:由于
gap的更新是在插入排序之前,因此当循环判断到gap == 1时,上一次进行的就是以1为gap增量的直接插入排序,此时序列已经有序,退出循环。
为什么要取gap = gap/3 + 1而不是gap = gap/3?
由于
最后gap要缩小到1进行直接插入排序,而如果我们选取gap = gap/3时,假设gap初始为6,第一次更新后gap=2,第二次更新后gap=0(向下取整),循环便结束了,并不会进行gap=1时的插入排序。因此,为了避免这种情况的发生,我们让gap = gap/3 + 1保证最后一次gap一定为1。
那为什么取gap = gap/2而不是gap = gap/2 + 1?
这种情况不需要处理的原因是
gap不可能等于0,因为进入循环的条件是gap>1,而gap只有等于0或1时gap/2才会为0。因此,无论gap初始为多少,最后一定都会在gap=1处停下。并且,当gap=2时,使用gap = gap/2 + 1会出现死循环/font>噢
- 每组之间进行的就是我们上面介绍的直接插入排序,不一样的是相邻元素的距离是gap而不是1。以下是gap = 3时的单趟希尔排序的动图过程:
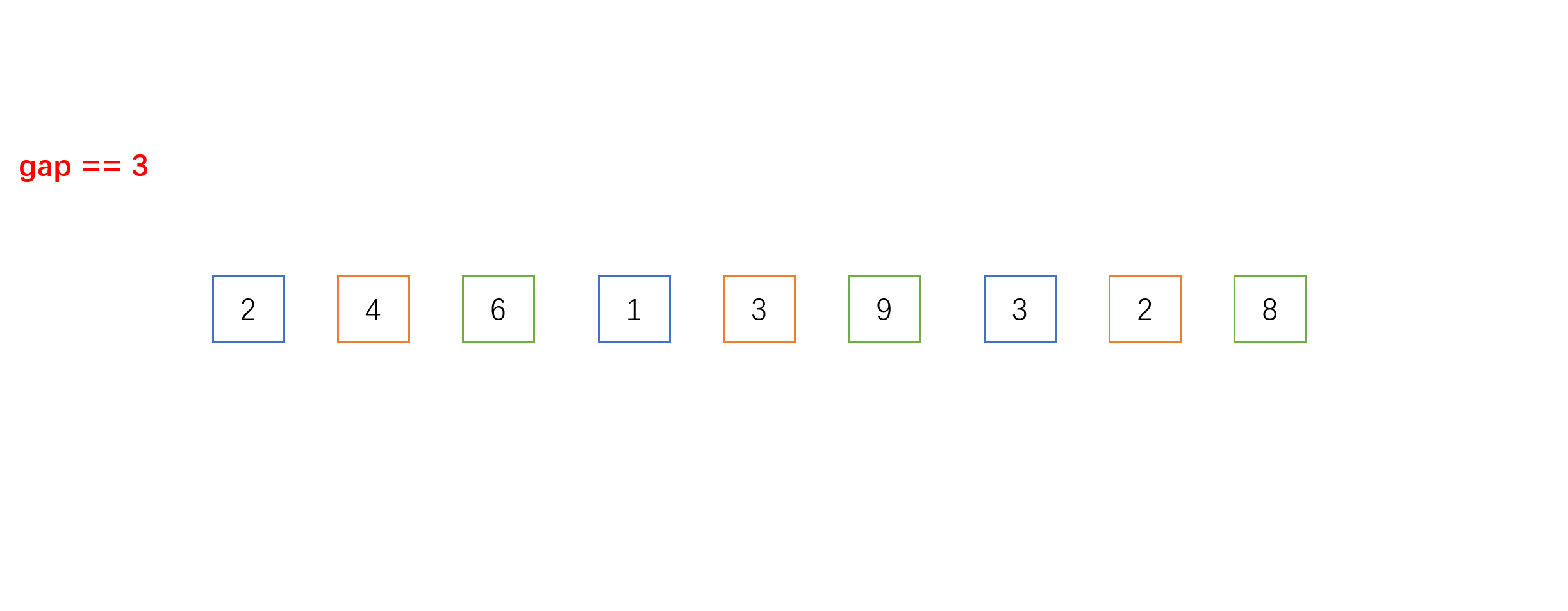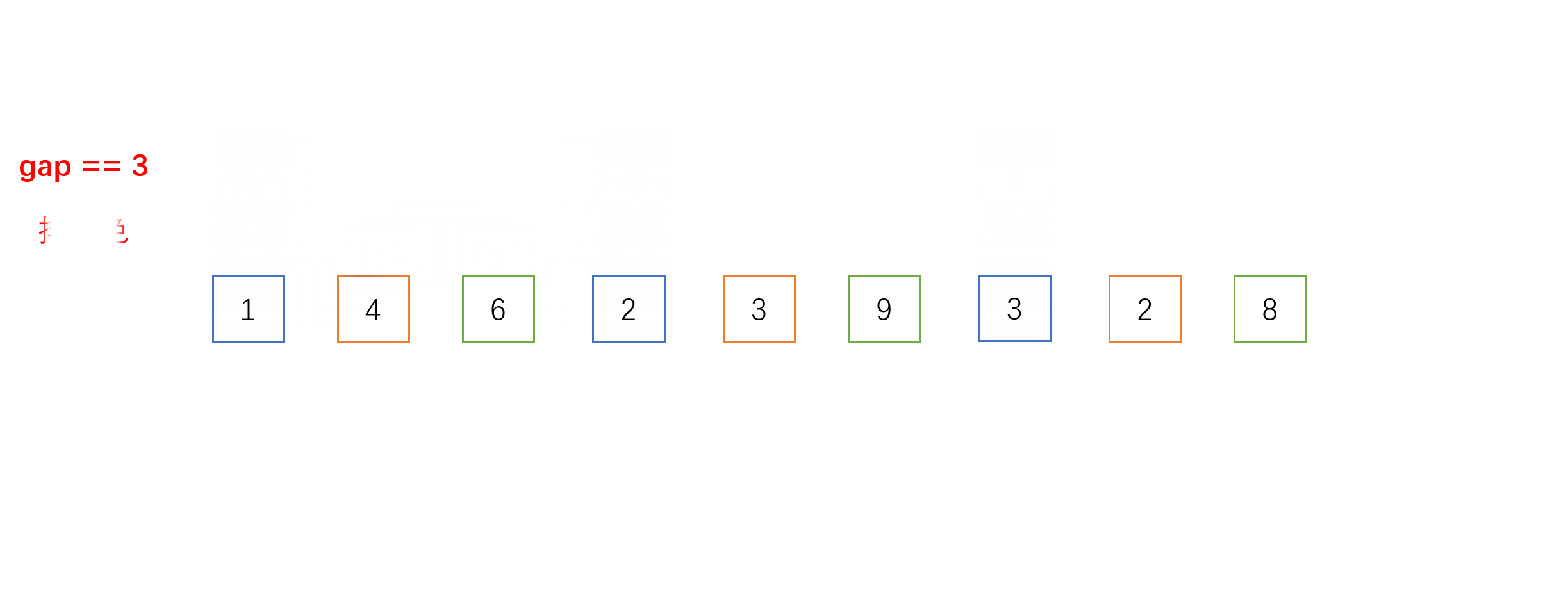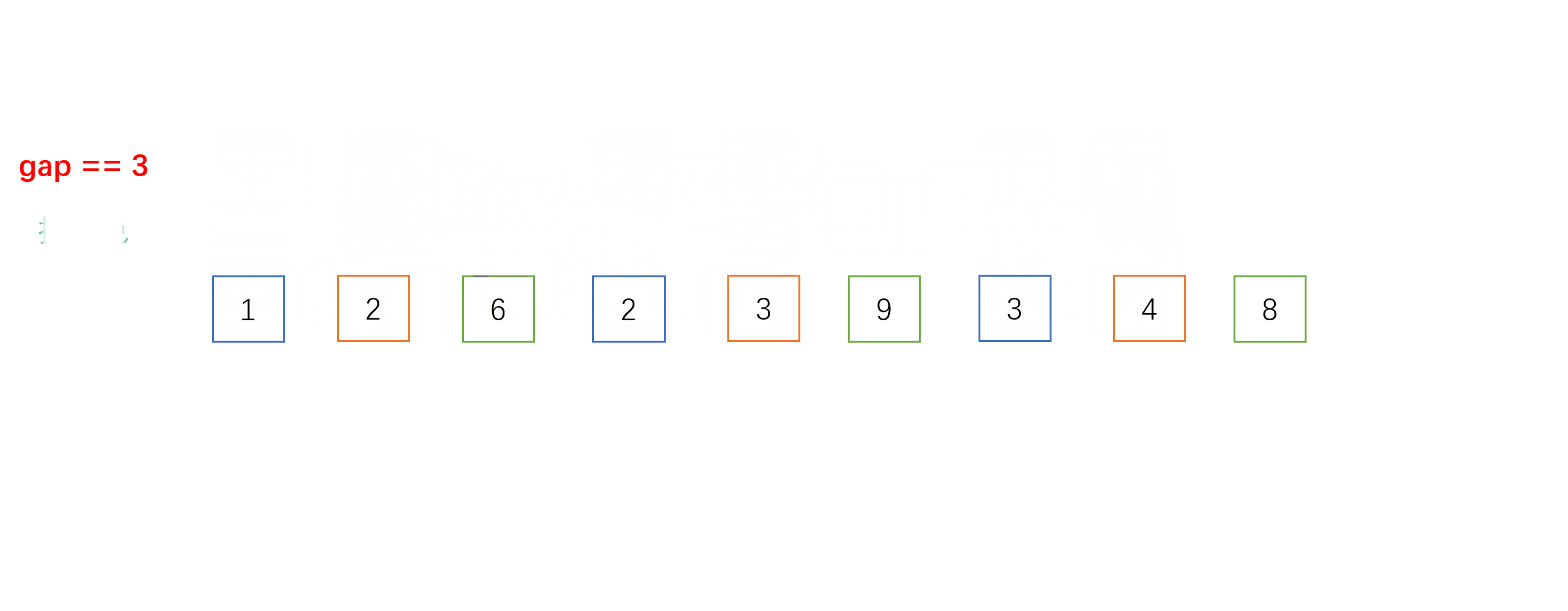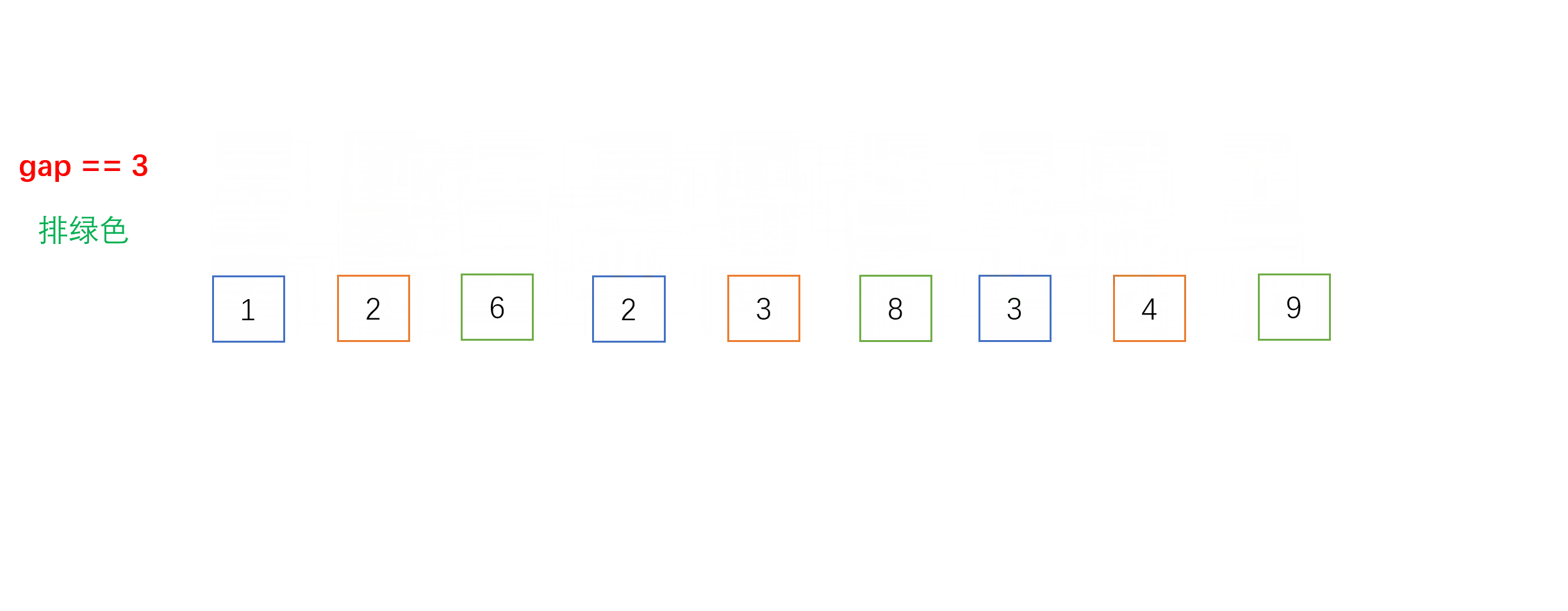
- 下面是希尔排序的全过程(以gap = gap/3 + 1为例):
- 通过观察,我们可以发现实际上
希尔排序就是直接插入排序的优化版。随着每一趟的分组排序,序列越来越接近有序。前面我们说过,直接插入排序在序列越接近有序的情况下效率越高,希尔排序就是通过每趟的预排序来使得序列越来越接近有序,从而提高直接插入排序的整体效率。 - 要点提炼:当gap > 1时,对序列进行分组预排序,目的是使得序列越来越接近有序;当gap == 1时,数组接近有序,此时进行直接插入排序效率大幅提高。
//写法1:一组一组排
void ShellSort1(int* a, int n)
{int gap = n;while (gap > 1){//1:gap > 1,预排序//2:gap == 1,直接插入排序gap = gap / 3 + 1; //缩小增量for (int j = 0; j < gap; j++) //一组一组进行插入排序,共gap组{//对当前组进行直接插入排序,组内相邻元素相距gap。//(其实就相当于把上面介绍的直接插入排序代码中的-1改成-gap即可)for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}
但是,上面的代码实际上还可以写得更加简洁
我们知道每个组的元素都相距gap,而组与组之间距离都为1。那么,我们实际上不用一组一组分开排,而是采用多组并排的方式,这样就可以少写一个for循环,代码如下
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
复杂度/稳定性分析
复杂度:
尽管上面的代码有多个循环嵌套,但这并不意味着希尔排序的效率低下。我们根据代码来分析一下希尔排序的时间复杂度,过程如下图所示:
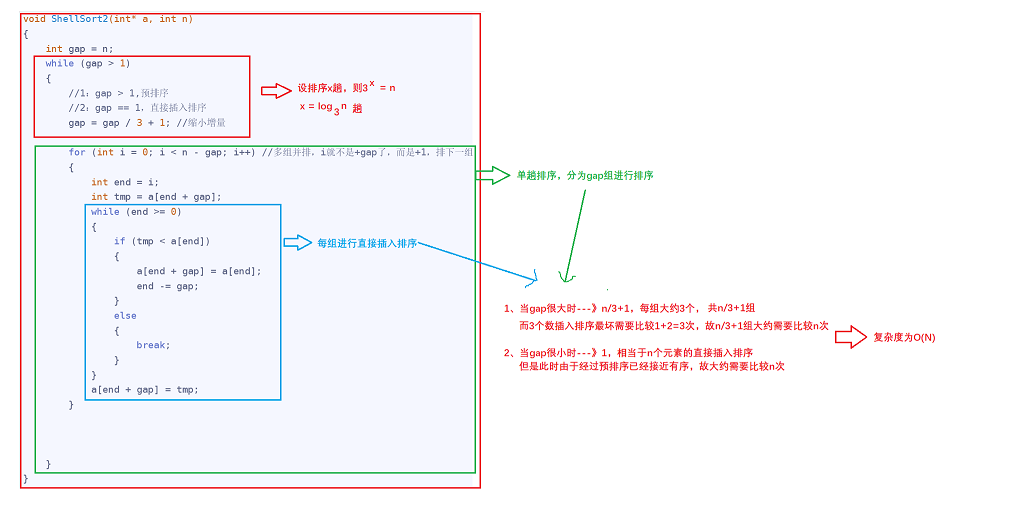
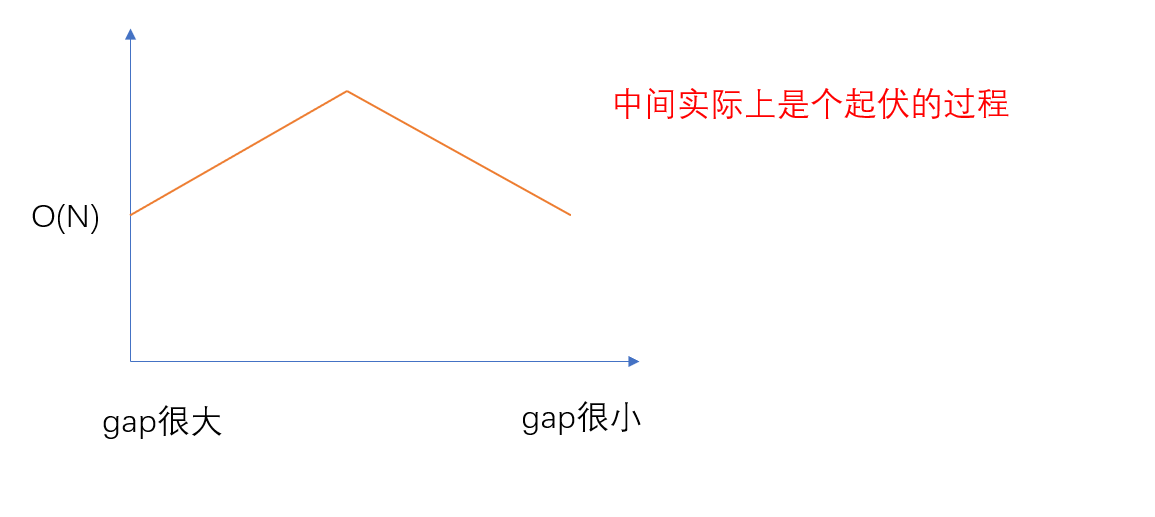
我们可以看到,在gap很大或者gap很小的情况下,每趟排序的时间复杂度为O(N),共进行log3n趟,那我们是不是可以认为希尔排序的时间复杂度为O(NlogN)?实际上并不行,因为当gap处于中间的过程时,时间复杂度的分析实际上是个很复杂的数学问题。每一趟预排序之后都对下一趟排序造成影响,这就好比叠buff的过程。
以下分别是两本书中对希尔排序时间复杂度的说法:
1、《数据结构(C语言版)》— 严蔚敏
2、《数据结构-用面相对象方法与C++描述》— 殷人昆
因为我们上面的gap是按照Knuth提出的方式取值的,并且Knuth进行了大量的试验统计,时间复杂度我们就按照:O(n^1.25)到O(1.6n^1.25)来进行取值。
然后就是空间复杂度,由于我们依旧只用到了常数级的辅助变量,因此空间复杂度为O(1)。
稳定性:
由于希尔排序是分组进行排序,当相同的数被分到不同组时,很可能就会改变相同的数的顺序,因此,希尔排序是不稳定的排序。

五、 选择排序
- 思想 : 每一次从待排序的数据元素中选出最小(升序)或最大(降序)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
- **选择过程:**以下是对某个序列进行选择排序的过程:
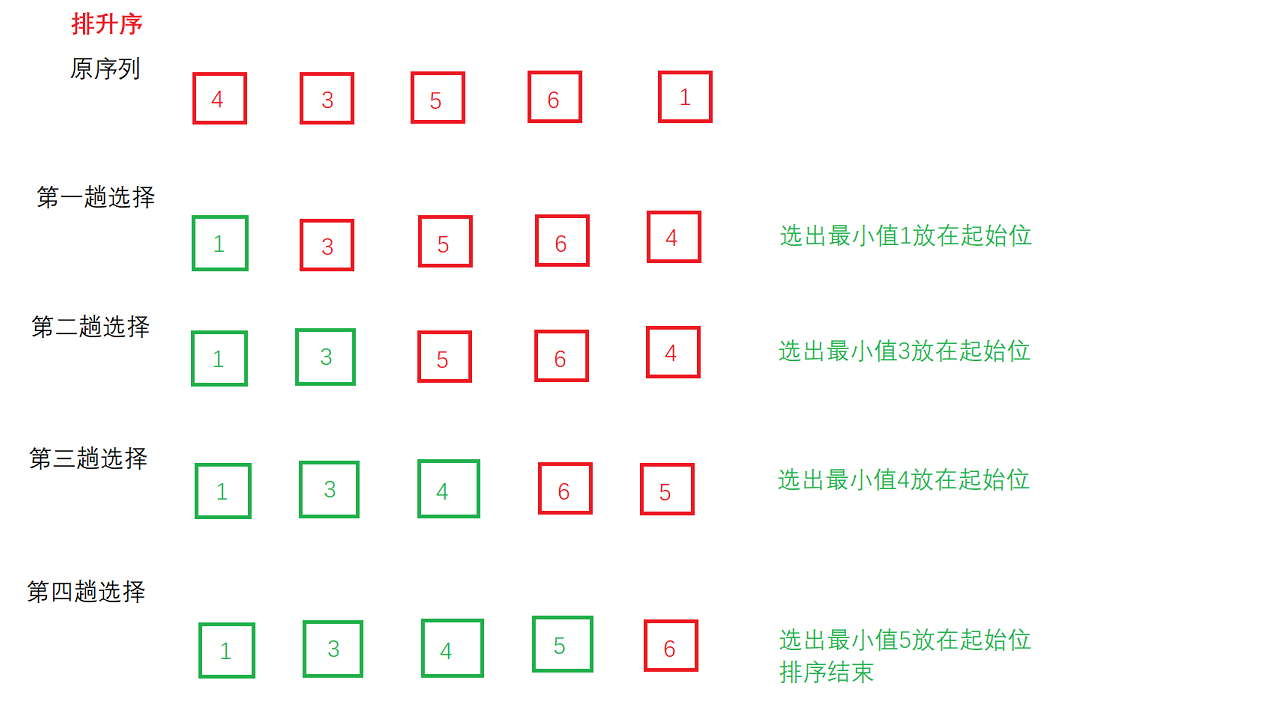
- **动图演示:**我们一样通过动图感受一下选择排序的过程:
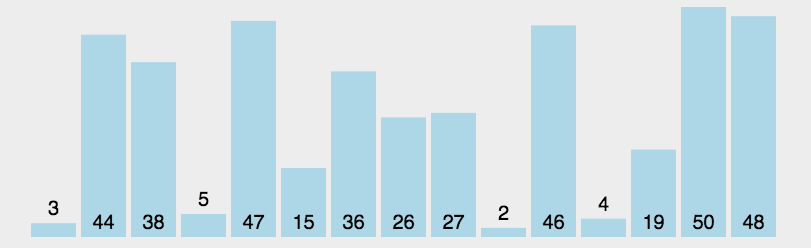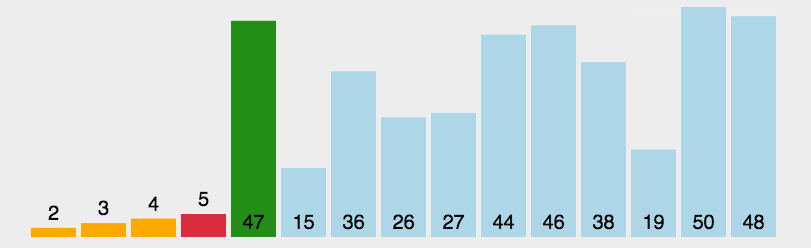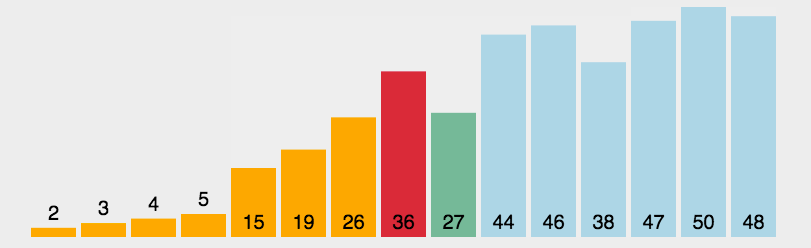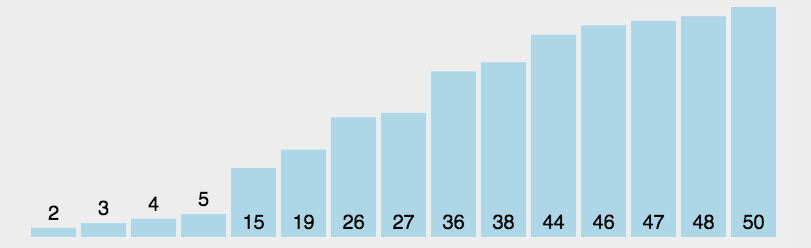
- **循环控制:**类似的,我们需要两层循环来控制选择排序的过程。
内层循环遍历序列找出最大/最小值,外层循环控制选择的次数。 - **外层循环结束条件:**每一次遍历完都可以选出一个数换到起始位置,一共N个数,故要选N-1次(最后一个数不需要选择)
for (int i = 0; i < n-1; i++) //外层循环,共要选择n-1次
{;
}
- **内层循环结束条件:**内层循环通过比较进行选数,一开始N个数需要比较N-1次,然后每趟结束后下一次选择的起始位置就往后移动一位,比较次数减1
for (int i = 0; i < n-1; i++) //外层循环,共选择n-1次
{for (int j = i + 1; j < n; j++) //内层循环,起始位置开始向后进行比较,选最小值{;}
}
- 完整代码:
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}void SelectSort(int* a, int n)
{for (int i = 0; i < n - 1; i++) //外层循环,共选择n-1次{int mini = i; //记录最小值的下标,初始为第一个数下标for (int j = i + 1; j < n; j++) //内层循环,起始位置开始向后进行比较,选最小值{if (a[mini] > a[j]) //比最小值小,交换下标{mini = j;}}swap(&a[mini], &a[i]); //将最小值与起始位置的数据互换}
}
- **时间/空间复杂度:**一共选了N-1次,每次选择需要比较N-1,N-2,N-3…次,加起来和冒泡一样时间复杂度为
;没有用到辅助空间,空间复杂度为
- **稳定性分析:**由于是选数交换,在交换的过程中很可能会打乱相同元素的顺序,例如下面这个例子:
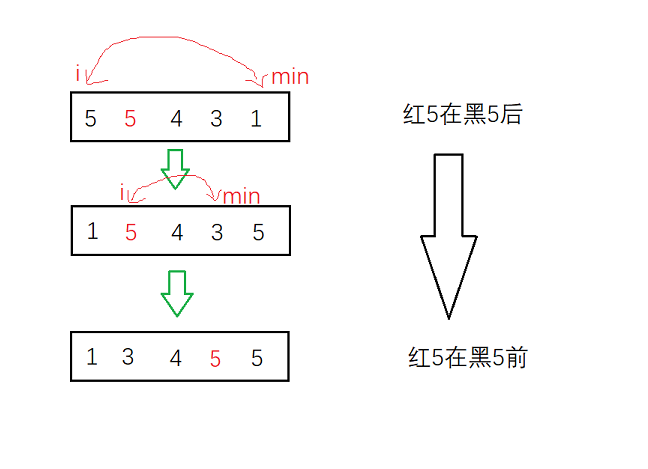
我们发现,在第一趟交换中,黑5被交换到了红5后面,在整个排序结束后,黑5依然在红5的后方,与最开始的顺序不一致。由此我们可以得出,选择排序是不稳定的排序。
六、各大排序算法的复杂度和稳定性
| 排序算法 | 时间复杂度(最好) | 时间复杂度(平均) | 时间复杂度(最坏) | 空间复杂度 | 稳定性 | 数据敏感度 |
|---|---|---|---|---|---|---|
| 冒泡排序 | 稳定 | 强 | ||||
| 选择排序 | 不稳定 | 弱 | ||||
| 直接插入排序 | 稳定 | 强 | ||||
| 希尔排序 | 不稳定 | 强 | ||||
| 堆排序 | 不稳定 | 弱 | ||||
| 快速排序 | 不稳定 | 强 | ||||
| 归并排序 | 稳定 | 弱 |
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位铁汁们的支持。文章有任何问题可以在评论区留言,小羊一定认真修改,写出更好的文章~~

















)




