自适应局部降噪滤波器

自适应局部降噪滤波器是一种信号处理技术，用于降低图像或信号中的噪声水平，同时保留图像或信号的细节。其原理基于局部区域内信号的统计特性和噪声的特征，通过动态调整滤波器的参数来适应不同区域的信号和噪声属性。
自适应局部降噪滤波器的基本原理：
**局部区域选择：**滤波器首先选择信号中的局部区域，例如使用一个固定大小的窗口或者动态选择尺寸以包含相邻像素或信号点。这个局部区域是用来估计噪声和信号特性的基础。
**估计信号和噪声特性：**在选定的局部区域内，通过统计方法（例如均值、方差等）对信号和噪声的特性进行估计。这些特性通常用于确定滤波器的参数，以便在滤波过程中更好地区分信号和噪声。
参数调整和滤波：基于对局部区域内信号和噪声特性的估计，滤波器动态调整其参数。这些参数可能包括滤波器的增益、阈值或者卷积核的权重等。滤波器根据这些参数对局部区域进行滤波，以抑制噪声并尽可能地保留信号的细节。
重复应用到整个信号或图像：上述步骤被迭代应用到整个信号或图像的每个局部区域，以处理整个信号并减少整体的噪声水平。

自适应局部降噪滤波器的关键在于其能够根据局部区域内信号和噪声的特性来自动调整滤波器参数，以更有效地降低噪声而不丢失重要的信号信息。这种方法常用于图像处理、音频处理和信号处理领域，用于提高图像质量或改善信号清晰度。

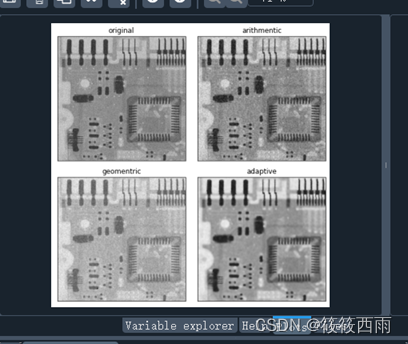
编写python代码，输出如下图所示的结果：

文件是一幅被均值为0，方差为1000的高斯噪声污染的图像。结果依次显示了算术均值滤波器、几何均值滤波器、自适应局部降噪滤波器对该图像滤波的结果。计算公式为：

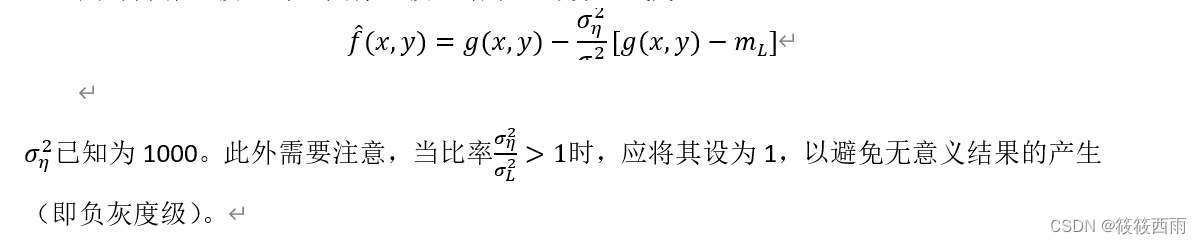
代码实现

import cv2
import numpy as np
import skimage
from matplotlib import pyplot as pltimg = cv2.imread('Fig0513.tif',0)
img_n = skimage.util.random_noise(img, mode='gaussian', seed=None, clip=False, mean=0, var=0.01)
img_n = 255*(img_n-img_n.min())/(img_n.max()-img_n.min())
img_n = img_n.astype(np.uint8)def calculate_sigma_eta(image):hist, bins = np.histogram(image.flatten(), bins=256, range=[0, 256], density=True)r = bins[:-1]m = np.sum(r * hist)sigma = np.sum((r - m) ** 2 * hist)return sigmadef calculate_sigma_sxy(block):hist, bins = np.histogram(block.flatten(), bins=256, range=[0, 256], density=True)r = bins[:-1]m = (r * hist).sum()sigma = ((r - m) ** 2 * hist).sum()return sigma, mdef adaptive_local_denoise(image, kernel, sigma_eta=1):epsilon = 1e-8height, width = image.shape[:2]m, n = kernel.shape[:2]padding_h = int((m - 1) / 2)padding_w = int((n - 1) / 2)image_pad = np.pad(image, ((padding_h, m - 1 - padding_h), \(padding_w, n - 1 - padding_w)), mode="edge")img_result = np.zeros(image.shape)for i in range(height):for j in range(width):block = image_pad[i:i + m, j:j + n]gxy = image[i, j]z_sxy = np.mean(block)sigma_sxy = np.var(block)rate = sigma_eta / (sigma_sxy + epsilon)if rate >= 1:rate = 1img_result[i, j] = gxy - rate * (gxy - z_sxy)return img_resultdef ArithmeticMeanAlogrithm(image):# 算术均值滤波new_image = np.zeros(image.shape)image = cv2.copyMakeBorder(image,1,1,1,1,cv2.BORDER_DEFAULT)for i in range(1,image.shape[0]-1):for j in range(1,image.shape[1]-1):new_image[i-1,j-1] = np.mean(image[i-1:i+2,j-1:j+2])new_image = (new_image-np.min(image))*(255/np.max(image))return new_image.astype(np.uint8)def GeometricMeanOperator(roi):roi = roi.astype(np.float64)p = np.prod(roi)return p ** (1 / (roi.shape[0] * roi.shape[1]))def GeometricMeanAlogrithm(image):# 几何均值滤波new_image = np.zeros(image.shape)image = cv2.copyMakeBorder(image, 1, 1, 1, 1, cv2.BORDER_DEFAULT)for i in range(1, image.shape[0] - 1):for j in range(1, image.shape[1] - 1):new_image[i - 1, j - 1] = GeometricMeanOperator(image[i - 1:i + 2, j - 1:j + 2])new_image = (new_image - np.min(image)) * (255 / np.max(image))return new_image.astype(np.uint8)# 自适应局部降噪滤波器处理高斯噪声
kernel = np.ones([7, 7])
img_arithmentic_mean = ArithmeticMeanAlogrithm(img_n)
img_geometric_mean = GeometricMeanAlogrithm(img_n)
img_adaptive_local = adaptive_local_denoise(img, kernel=kernel, sigma_eta=1000)plt.figure(figsize=(7,7))plt.subplot(2,2,1),plt.imshow(img, cmap = 'gray'),plt.title('original')
plt.xticks([]),plt.yticks([])
plt.subplot(2,2,2),plt.imshow(img_arithmentic_mean, cmap = 'gray'),plt.title('arithmentic')
plt.xticks([]),plt.yticks([])
plt.subplot(2,2,3),plt.imshow(img_geometric_mean, cmap = 'gray'),plt.title('geomentric')
plt.xticks([]),plt.yticks([])
plt.subplot(2,2,4),plt.imshow(img_adaptive_local, cmap = 'gray'),plt.title('adaptive')
plt.xticks([]),plt.yticks([])
plt.tight_layout()
plt.show()

实验结果

自适应滤波器是指根据环境的改变，使用自适应算法来改变滤波器的参数和结构的滤波器。一般情况下，不改变自适应滤波器的结构。而自适应滤波器的系数是由自适应算法更新的时变系数。即其系数自动连续地适应于给定信号，以获得期望响应。自适应滤波器的最重要的特征就在于它能够在未知环境中有效工作，并能够跟踪输入信号的时变特征。

自适应局部滤波器设计流程

① 生成高斯噪声
设计出高斯噪声，并添加到原图像中。
②设计均值滤波器
设计过程为：取出当前n*n阶滤波器对应的像素点，求其均值，并将结果放至结果矩阵中，输出。
③设计自适应均值滤波器
设计过程为：求噪声方差；以矩阵为整体运算，求出n阶滤波器对应的像素点像素的均值，方差；将局部方差与噪声方差进行比较，按照规则计算新的像素，并存在结果矩阵中，输出。