问题一要求在特定区域内部署两个边缘服务器，以便根据计算需求分布覆盖最大的计算需求。每个边缘服务器都有一个覆盖半径为1。目标是确定两个边缘服务器的位置，以覆盖最大的计算需求。假设边缘服务器的位置位于网格的中心，每个网格内的计算需求在附件中提供（Attachment 1_Computational Demand Distribution Data.csv）。
要求使用QUBO模型解决此问题，并使用Kaiwu SDK的模拟退火求解器和CIM模拟器进行求解。需要提供部署边缘服务器的坐标，这些服务器可以覆盖最大计算需求，以及相应的总计算需求覆盖量。
这个问题的关键在于理解和转换问题为一个适合的QUBO模型，并有效地使用Kaiwu SDK来找到最佳解决方案。接下来，我们通过对附件中的计算需求分布数据对分析，以开始建模分析。
数据集中包含了三列：
X-axis：表示网格的X轴坐标。
Y-axis：表示网格的Y轴坐标。
Amount of Computational Demands：表示在该网格位置的计算需求量。
数据可视化如下图

这幅图展示了计算需求在不同网格位置的分布情况。图中每个单元格代表一个网格点，其颜色的深浅表示该位置的计算需求量。颜色越深的区域表示计算需求越高。
通过观察这幅图，我们可以发现计算需求在不同网格之间的分布不均。这种分布对于确定两个边缘服务器的最佳部署位置至关重要。理想情况下，我们希望将服务器部署在计算需求集中且相对较高的区域，以最大化覆盖范围和总计算需求量。
接下来，我们可以根据这个分布，结合QUBO模型和模拟退火算法，来确定两个边缘服务器的最佳部署位置。
为了解决问题一，我们需要使用这些数据来构建QUBO模型，从而找出能够覆盖最大计算需求的两个边缘服务器的最佳位置。QUBO模型的构建将基于以下原则：
二元决策变量：为每个网格位置定义一个二元变量（0或1），表示是否在该位置部署边缘服务器。
目标函数：构建一个目标函数来最大化覆盖的计算需求。这将涉及到考虑边缘服务器的覆盖半径和每个网格的计算需求。
约束：虽然QUBO模型通常不涉及显式约束，但我们需要确保模型反映出只能部署两个边缘服务器的条件。
​
构建了QUBO（Quadratic Unconstrained Binary Optimization）矩阵，这是解决问题一所需的关键步骤。这个矩阵的构建基于以下原则：
矩阵大小：QUBO矩阵的大小与网格点的数量相同。在这种情况下，每个网格点对应一个二进制决策变量（0或1），表示是否在该位置部署一个边缘服务器。
奖励机制：QUBO矩阵的对角线元素代表在相应位置部署边缘服务器的奖励，与该位置的计算需求成比例。因此，计算需求越高的位置，其对应的矩阵元素值越小（在这里使用负值表示奖励，因为我们是在最小化QUBO）。
约束条件：QUBO矩阵的非对角线元素用于实施约束，即总共只能部署两个边缘服务器。通过增加矩阵的非对角线元素的值，可以对部署超过两个服务器的情况施加惩罚。
接下来的步骤是使用Kaiwu SDK的模拟退火求解器和CIM模拟器来求解这个QUBO矩阵，找到最优的服务器部署方案。
搜索结果：

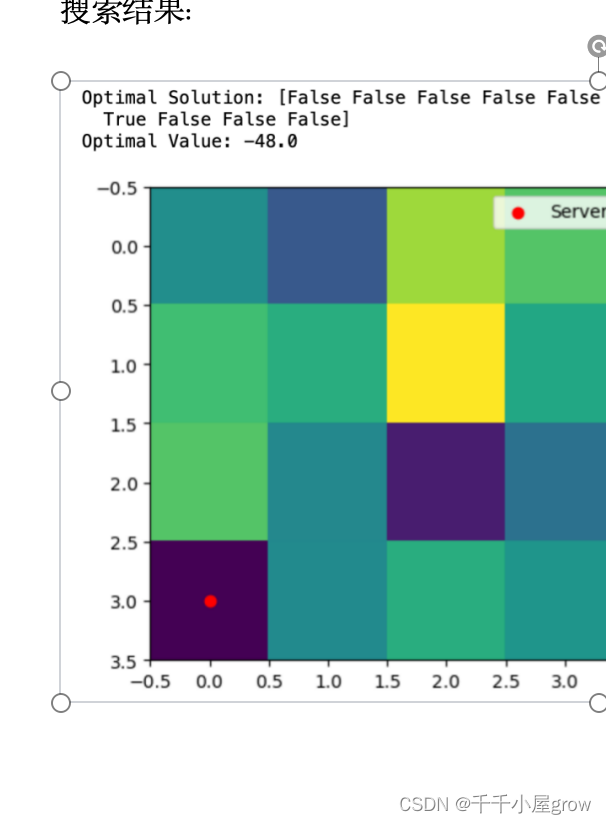
最优解：显示了在哪些网格位置部署边缘服务器，True 表示在相应位置部署服务器。
最优值：显示了该解的QUBO能量值，代表了被覆盖的计算需求总量。
在可视化中，计算需求分布以颜色深浅展示，而边缘服务器的位置则用红色标记。

问题二：

问题二所需的三个数据集：
用户数据（Attachment 2）：包含每个用户位置的X坐标、Y坐标，以及该位置的计算需求量。
边缘服务器数据（Attachment 3）：包含每个候选边缘服务器位置的编号、X坐标、Y坐标，以及该位置的固定成本。
云服务器数据（Attachment 4）：包含云服务器的编号、X坐标、Y坐标。
为了解决问题二，我们需要进行步骤：
数据分析与准备：理解并分析用户的计算需求分布、边缘服务器的候选位置以及它们的固定成本，以及云服务器的位置。
问题建模：使用QUBO模型来表示问题，这将包括确定边缘服务器的最优部署位置、计算成本、传输成本，以及确保每个用户的需求都得到满足的同时最小化总成本。
求解模型：使用模拟退火求解器或CIM模拟器求解QUBO模型，以确定最优的计算网络布局。
结果分析：分析求解器得出的结果，确定边缘服务器的部署位置和数量，以及用户与服务器之间的连接方式。
先进行数据可视化

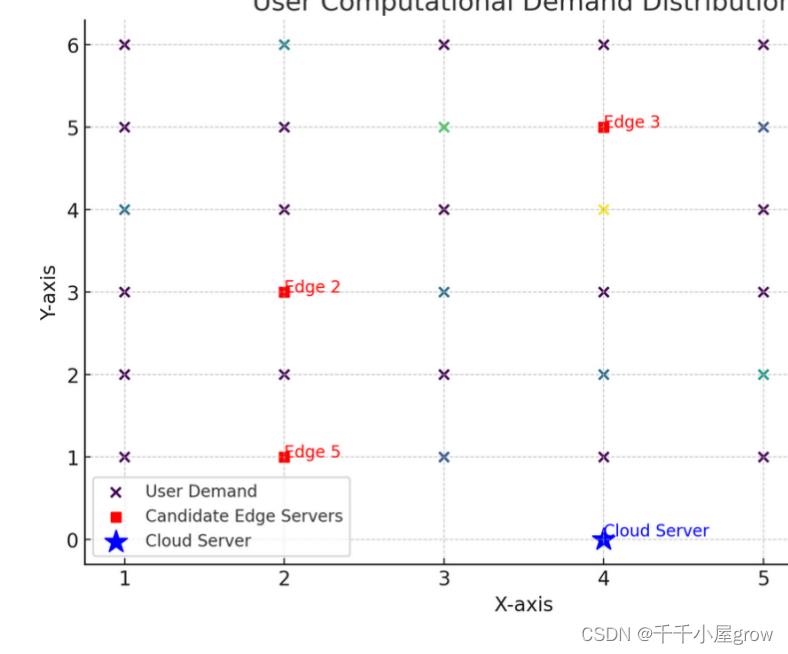
数据可视化展示了以下信息：
用户计算需求分布：以不同颜色的点表示，颜色深浅代表不同的计算需求量。这些点分布在整个区域中，显示了每个位置的计算需求。
边缘服务器候选位置：用红色方形标记表示。这些位置是部署边缘服务器的潜在选项，每个位置都有相应的固定成本。
云服务器位置：用蓝色星形标记表示。云服务器的位置是固定的，其计算资源容量被认为是无限的
下面进行数据分析
计算需求分布：需求分布不均，有些区域的需求量显著高于其他区域。在决定边缘服务器的部署位置时，这些高需求区域应被优先考虑。
边缘服务器的位置选择：候选位置的选择需要考虑覆盖高需求区域的能力以及与这些区域的距离，因为传输成本与距离成正比。
成本效益分析：在选择部署边缘服务器的位置时，需要权衡固定成本和计算成本。位置越靠近用户，传输成本越低，但也可能意味着较高的固定成本。

· 目标函数：目标函数需要最小化总成本，包括固定成本、计算成本和传输成本。
·约束条件：
每个用户只能连接到一个服务器。
边缘服务器的计算资源容量不得超过其限制。
下面进行代码编写和分析
固定成本：每个候选边缘服务器位置的固定成本直接添加到QUBO矩阵的对应位置。
计算成本和传输成本：需要根据用户与服务器之间的连接决策来计算。这可能涉及到复杂的计算，尤其是在处理用户到边缘服务器和边缘服务器到云服务器的传输成本时。
约束条件：确保每个用户只连接到一个服务器，并且边缘服务器的计算资源容量不被超过。
构建完整的QUBO模型涉及到大量的计算和逻辑判断，考虑到模型的复杂性，可能需要进行一些简化或近似，以确保模型可以有效地被求解器处理。
完整内容见简介

完整的问题二求解代码

首先，我们需要定义一些辅助函数来计算距离和成本

def euclidean_distance(x1, y1, x2, y2):
“”“计算两点之间的欧几里得距离”“”
return round(((x1 - x2)**2 + (y1 - y2)**2)**0.5, 2)

def compute_cost(QUBO, solution, data_user, data_edge, data_cloud):
“”“计算给定解决方案的总成本”“”
total_cost = 0
N = len(data_edge)
M = len(data_user)
cloud_x, cloud_y = data_cloud.iloc[0][‘X-axis’], data_cloud.iloc[0][‘Y-axis’]

# 固定成本和计算成本
for i in range(N):if solution[i] == 1:total_cost += data_edge.iloc[i]['Fixed Cost']for j in range(M):if solution[N + i * M + j] == 1:total_cost += 2 * data_user.iloc[j]['Amount of Computational Demands']  # 边缘服务器计算成本# 传输成本
for j in range(M):user_x, user_y = data_user.iloc[j]['X-axis'], data_user.iloc[j]['Y-axis']connected_to_edge = Falsefor i in range(N):if solution[N + i * M + j] == 1:edge_x, edge_y = data_edge.iloc[i]['X-axis'], data_edge.iloc[i]['Y-axis']total_cost += euclidean_distance(user_x, user_y, edge_x, edge_y) * data_user.iloc[j]['Amount of Computational Demands']  # 用户到边缘的传输成本total_cost += euclidean_distance(edge_x, edge_y, cloud_x, cloud_y) * data_user.iloc[j]['Amount of Computational Demands']  # 边缘到云的传输成本connected_to_edge = Truebreakif not connected_to_edge:total_cost += 2 * euclidean_distance(user_x, user_y, cloud_x, cloud_y) * data_user.iloc[j]['Amount of Computational Demands']  # 用户到云的传输成本return total_cost

构建QUBO矩阵

N = len(data_edge)
M = len(data_user)
num_variables = N + N * M # 每个边缘服务器位置一个变量 + 每个用户对每个边缘服务器的连接变量
QUBO = np.zeros((num_variables, num_variables))

填充QUBO矩阵

固定成本

for i in range(N):
QUBO[i, i] = data_edge.iloc[i][‘Fixed Cost’]

连接决策（暂时不考虑容量限制和其他约束）

for i in range(N):
for j in range(M):
QUBO[N + i * M + j, N + i * M + j] = 2 * data_user.iloc[j][‘Amount of Computational Demands’] # 边缘服务器计算成本

运行模拟退火算法

init_state = np.random.choice([0, 1], size=num_variables)
result = dual_annealing(lambda x: compute_cost(QUBO, x > 0.5, data_user, data_edge, data_cloud), bounds=[(0, 1)] * num_variables, x0=init_state)

输出结果

optimal_solution = result.x > 0.5
optimal_value = compute_cost(QUBO, optimal_solution, data_user, data_edge, data_cloud)

print(“Optimal Solution:”, optimal_solution)
print(“Optimal Value:”, optimal_value)