系列文章目录

1. 机器学习实验一：线性回归
2. 机器学习实验二：决策树模型
3. 机器学习实验三：支持向量机模型
4. 机器学习实验四：贝叶斯分类器
5. 机器学习实验五：集成学习
6. 机器学习实验六：聚类

---

---

一、实验目的

（1）掌握线性回归的基本原理；
（2）掌握线性回归的求解方法；
（3）掌握梯度下降法原理；
（4）掌握最小二乘法。

二、实验原理

1.线性回归

线性回归的任务是找到一个从输入特征空间X到输出特征空间Y的最优的线性映射函数简单来说给定d个属性描述的示例x=(x1,x2,…,xd)，其中xi表示x在第i个属性上的取值。线性模型试图学到通过属性的线性组合来进行预测的函数，即：
写成向量形式：
其中，w=(w1,w2,…,wd)，wT表示w的转置。
我们可以使用均方误差确定w和b，均方误差是回归任务中最常用的性能度量，我们试图通过均方误差最小来求解w和b，即：
我们称上式为代价函数或损失函数，我们只需要使代价函数最小即可。

2.梯度下降法

函数沿着导数方向是变化最快的，为了更快地达到优化目标，沿着负梯度方向搜寻w，b使得代价函数最小，即使用梯度下降法更新权重即可求出w和b。
梯度就是多元函数的偏导数，我们求出代价函数对w，b的偏导数，即：

沿着负梯度方向搜寻w，b使得代价函数最小，即使用梯度下降法更新权重：

η为学习率，随机初始化w，b，通过不断地迭代上述2个更新公式计算w，b的最优值。

3.最小二乘法

使用最小二乘法求解w，b，即令代价函数对w，b的偏导数为0，这种基于均方误差进行线性模型求解的方法称为最小二乘法。
w，b的计算公式为：


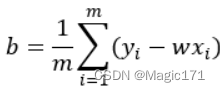
可以看出最小二乘法是梯度下降法的一种特殊情况，很多函数解析不出导数等于零的点，梯度下降法是求解损失函数参数更常用的方法。

三、实验内容

准备数据，np.random,rand()产生一组随机数据x，根据y=wx+b，产生数据y，并用np.random.rand()添加随机噪声，y=wx+b+噪声，得到数据集(x,y)；
建立线性模型，y_pre=wx+b；
采用均方误差，构建损失函数；
训练模型，梯度下降法进行优化权重求解w和b；
直接使用最小二乘法求解w和b，并与梯度下降法求解的w和b进行比较；
绘制样本点，预测直线。

四、实验步骤

1. 随机生成数据集

使用np.arange()产生0到10、步长为0.2的数据x，再生成与x相同长度的全1向量，两者行叠加再转置得到(1,wT)，记为input_data。设置w和b，令y=wx+b+random噪声，记为target_data。input_data和target_data组成数据集。代码如下：

# 构造训练数据
x = np.arange(0., 10., 0.2)
m = len(x)
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T
w = 2
b = 5
target_data = w * x + b + np.random.randn(m)

2. 梯度下降法

设学习率η=0.001，随机初始化w和b，设(b,w)T向量为theta。沿着负梯度方向搜寻w，b使得代价函数最小。在每次循环中，更新w，b的值，并打印。当循环次数超过设定最大次数或w和b达到收敛条件时，退出循环。代码如下：

# 终止条件
loop_max = 1e4  # 最大迭代次数
epsilon = 1e-3  # 收敛条件最小值# 初始化权值
np.random.seed(0)
theta = np.random.randn(2)
alpha = 1e-3  # 步长，也叫学习率
diff = 0.
error = np.zeros(2)
count = 0  # 循环次数
finish = 0  # 终止标志# 迭代
while count < loop_max:count += 1# 在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算sum_m = np.zeros(2)for i in range(m):diff = (np.dot(theta, input_data[i]) - target_data[i]) * input_data[i]# 当alpha取值过大时,sum_m会在迭代过程中会溢出sum_m = sum_m + diff# 注意步长alpha的取值,过大会导致振荡theta = theta - alpha * sum_m# 判断是否已收敛if np.linalg.norm(theta - error) < epsilon:finish = 1breakelse:error = theta# 打印迭代次数、更新后的w和bprint('迭代次数 = %d' % count, '\t w:', theta[1], '\t b:', theta[0])print('迭代次数 = %d' % count, '\t w:', theta[1], '\t b:', theta[0])

3. 最小二乘法

使用Python第三方库——scipy中的统计模块——stats中的linregress()计算两组测量值x和target_data的线性最小二乘回归。代码如下：

# 用scipy线性最小二乘回归进行检查
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print('使用最小二乘法计算，斜率 = %s 截距 = %s' % (slope, intercept))

4. 绘图

使用Python第三方库——matplotlib中的plot()进行绘图。样本点用蓝色星形点表示，梯度下降法得到的预测直线用红色实线表示，而最小二乘法得到的预测直线用绿色实线表示。代码如下：

# 用plot进行展示
plt.scatter(x, target_data, color='b', marker='*')
# 梯度下降法
plt.plot(x, theta[1] * x + theta[0], label='gradient descent', color='red')
# 最小二乘法
plt.plot(x, slope * x + intercept, label='least square', color='green')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Experiment 1: Linear regression')
plt.savefig('result.png')
plt.show()

总结

以上就是今天要讲的内容，机器学习实验一：线性回归