1.存储结构

1.邻接矩阵

图的邻接矩阵表示法（Adjacency Matrix）也称作数组表示法。它采用两个数组来表示图：

一个是用于存储顶点信息的一维数组；另一个是用于存储图中顶点之间关联关系的二维数组，这个关联关系数组被称为邻接矩阵。        

若图G是一个具有n个顶点的无权图，G的邻接矩阵是具有如下性质的n×n矩阵A：

网的邻接矩阵可定义为：

#define MaxVertexNum 100       /*最大顶点数设为100*/
typedef char VertexType;           /*顶点类型设为字符型*/
typedef int EdgeType;                 /*边的权值设为整型*/
typedef struct 
{	VertexType vexs[MaxVertexNum]; /*顶点表*/EdgeType edges[MaxVertexNum][MaxVertexNum];  /*邻接矩阵，即边表*/int n,e;                       /*顶点数和边数*/
}MGraph;                              /*Maragh是以邻接矩阵存储的图类型*/

邻接矩阵法的特点

1、存储空间：

对于无向图而言， 它的邻接矩阵是对称矩阵（因为若（vi，vj）∈E（G），则（vj，vi）∈E（G））

因此我们可以采用特殊矩阵的压缩存储法，即只存储其下三角即可，这样，一个具有n个顶点的无向图G它的邻接矩阵需要n（n-1）/2个存储空间。

但对于有向图而言，其中的弧是有方向的， 即若<vi，vj>∈E（G），不一定有<vj，vi>∈E（G），因此有向图的邻接矩阵不一定是对称矩阵，对于有向图的邻接矩阵的存储则需要n2个存储空间。

邻接矩阵的存储空间只和顶点个数有关，和边数无关

2、便于运算：

采用邻接矩阵表示法，邻接矩阵表示法适合于以顶点为主的运算。便于判定图中任意两个顶点之间是否有边相连，即根据A［i，j］=0或1来判断。另外还便于求得各个顶点的度。

对于无向图而言，其邻接矩阵第i行元素之和就是图中第i个顶点的度：

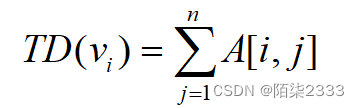
对于有向图而言，其邻接矩阵第i行元素之和就是图中第i个顶点的出度：

对于有向图而言，其邻接矩阵第i列元素之和就是图中第i个顶点的入度：

void CreateMGraph(MGraph *G)
{  int i, j, k;    printf("请输入顶点数和边数(输入格式为:顶点数,边数):\n");scanf("%d,%d",&(G->n),&(G->e));          /*输入顶点数和边数*/printf(“请输入顶点信息(输入格式为: <回车>顶点号):\n");for (i=0;i<G->n;i++)  scanf("\n%c", &(G->vexs[i]));       /*输入顶点信息，建立顶点表*/for (i=0;i<G->n;i++)for (j=0;j<G->n;j++)  G->edges[i][j]=0;               /*初始化邻接矩阵*/printf("请输入每条边对应的两个顶点的序号(输入格式为:i,j):\n");for (k=0;k<G->e;k++){	scanf("%d,%d",&i,&j);   /*输入e条边，建立邻接矩阵*/G->edges[i][j]=1;        /*若此处加入G->edges[j][i]=1;，则为无向图的邻接矩阵存储建立*/}
}

2.邻接表

图的邻接表的存储结构是一种顺序分配和链式分配相结合的存储结构，包括两个部分，一部分是数组，一部分是链表图的链式存储结构。          

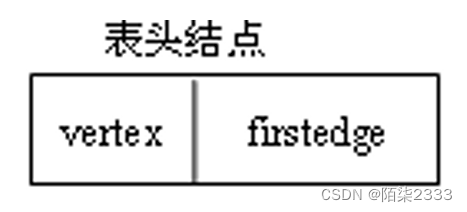
1）以一个数组来存储图中所有的顶点信息，数组中每个元素表示图中一个顶点，在邻接表中又称作表头结点，表头结点的结构，vertex域用来存储顶点自身的信息，firstedge域是一个指针，指向一个链表（即与该顶点相关的边链表）。

 对于无向图，第i个链表将图中与顶点νi相邻接的所有顶点链接起来，也就是链表中的每个结点表示了与顶点νi相关的边。

对于有向图的第i个链表有两种构造方式，一种是链接以顶点νi 为尾的所有结点；另外也可以链接以顶点νi 为头的所有结点。为了区别，以后者构造邻接表被称之为有向图的逆邻接表。

核心思想:对具有n个顶点的图建立n个线性链表存储该图

n个头结点之间为一数组结构

1.每一个链表前面设置一个头结点，用来存放一个顶点的数据信息，称之为顶点结点。其构造为

其中，vertex域存放某个顶点的数据信息；  firstedge域指向链表中第一个顶点（即与顶点vi邻接的第一个邻接点）。

2.第i个链表中的每一个链结点(称之为表结点)表示以第i个顶点为出发点的一条边；边结点的构造为

其中，链表中的每个结点在邻接表中又称为表结点，具有相同的结构。adjvex域称为顶点域，它存储了与顶点νi相邻接的顶点在顶点数组中的序号；next域称为链域，存储一个指针，它链接了与顶点νi相邻接的顶点的表结点；info是信息域，可以存储与边相关的一些信息，例如对于带权图可以存储边的权值。

typedef struct node		/*表结点*/
{   int adjvex;                     	/*邻接点域*/struct node  * next;      /*指向下一个邻接点的指针域*//*  int info；                若要表示边上信息，则应增加一个数据域info*/
}EdgeNode;       
typedef struct vnode 	      	/*表头结点*/
{   VertexType vertex;           	/*顶点域*/EdgeNode  * firstedge;      	/*边表头指针*/
}VertexNode;   
typedef struct
{	VertexNode adjlist[MaxVertexNum];     /*邻接表*/int n, e;                             		           /*顶点数和边数*/
}ALGraph;      		/*ALGraph是以邻接表方式存储的图类型*/

邻接表与邻接矩阵比较：

若无向图有n个顶点、e条边，则它的邻接表需要n个头结点和2e个表结点

若有向图有n个顶点、e条边，则它的邻接表需要n个头结点和e个表结点

而邻接矩阵需要n方个数组单元

所以如果边比较少，邻接表更节省空间

联系：邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元素的个数。 区别：

① 对任一确定的无向图，邻接矩阵是唯一的(行列号与顶点编号一致)，但邻接表不唯一(链接次序与顶点编号无关)。

② 邻接矩阵的空间复杂度为O(n2)，而邻接表的空间复杂度为O(n+e)/O(n+2e)。

用途：邻接矩阵多用于稠密图的存储(e接近n(n-1)/2)；而邻接表多用于稀疏图的存储(e<<n2)。

void CreateALGraph(ALGraph *G)
{   int i,j,k;	    EdgeNode * s;printf("请输入顶点数和边数(输入格式为:顶点数,边数)：\n");scanf("%d, %d", &(G->n), &(G->e));   /*读入顶点数和边数*/printf(“\n请输入顶点信息(输入格式为: <回车>顶点号)：\n");for (i = 0; i < G->n; i++)                 	/*建立有n个顶点的顶点表*/{        scanf(“\n%c", &(G->adjlist[i].vertex));   	/*读入顶点信息*/G->adjlist[i].firstedge = NULL;   /*顶点的边表头指针设为空*/}printf(“\n请输入边的信息(输入格式为:i,j)：\n");for (k=0; k<G->e; k++)                     /*建立边表*/{       scanf("%d, %d", &i, &j); /*读入边<Vi,Vj>的顶点对应序号*/s = (EdgeNode*)malloc(sizeof(EdgeNode));  /*生成新边表结点s*/s->adjvex = j;                        	/*邻接点序号为j*/s->next = G->adjlist[i].firstedge;/*将新边表结点s用头插法插入到顶点Vi 的边表头部*/ G->adjlist[i].firstedge = s;}
}

typedef struct node		/*表结点*/
{   int adjvex;                     	/*邻接点域*/struct node  * next;      /*指向下一个邻接点的指针域*//*  int info；                若要表示边上信息，则应增加一个数据域info*/
}EdgeNode;       
typedef struct vnode 	      	/*表头结点*/
{   VertexType vertex;           	/*顶点域*/EdgeNode  * firstedge;      	/*边表头指针*/
}VertexNode;   
typedef struct
{	VertexNode adjlist[MaxVertexNum];     /*邻接表*/int n, e;                             		           /*顶点数和边数*/
}ALGraph;      		/*ALGraph是以邻接表方式存储的图类型*/

无向图的度        

在无向图的邻接表中，顶点vi的度恰好就是第i个边链表上结点的个数。

有向图的度        

在有向图中，第i个边链表上顶点的个数是顶点vi的出度，只需通过表头向量表中找到第i个顶点的边链表的头指针，实现顺链查找即可。        

求得第i个顶点的入度，也必须遍历整个邻接表，在所有边链表中查找邻接点域的值为i的结点并计数求和。由此可见， 对于用邻接表方式存储的有向图，求顶点的入度并不方便， 它需要通过扫描整个邻接表才能得到结果。

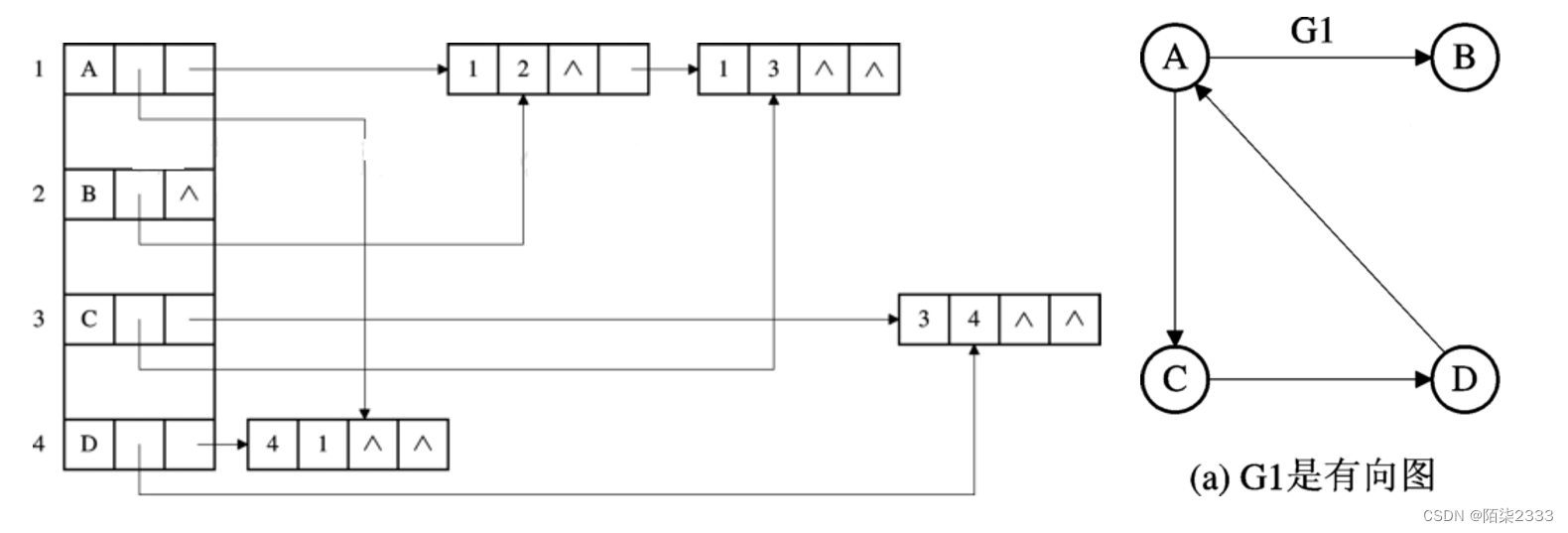
一种解决的方法是逆邻接表法，我们可以对每一顶点vi再建立一个逆邻接表，即对每个顶点vi建立一个所有以顶点vi为弧头的弧的表，如图所示。

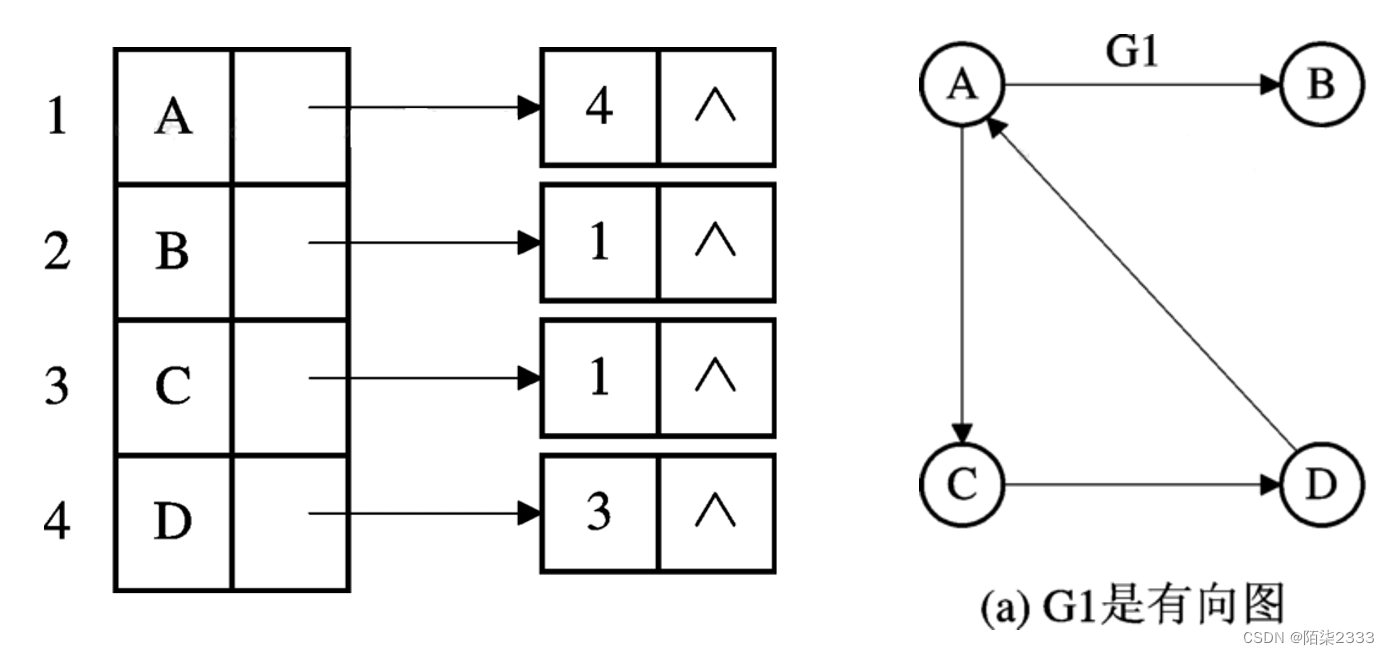
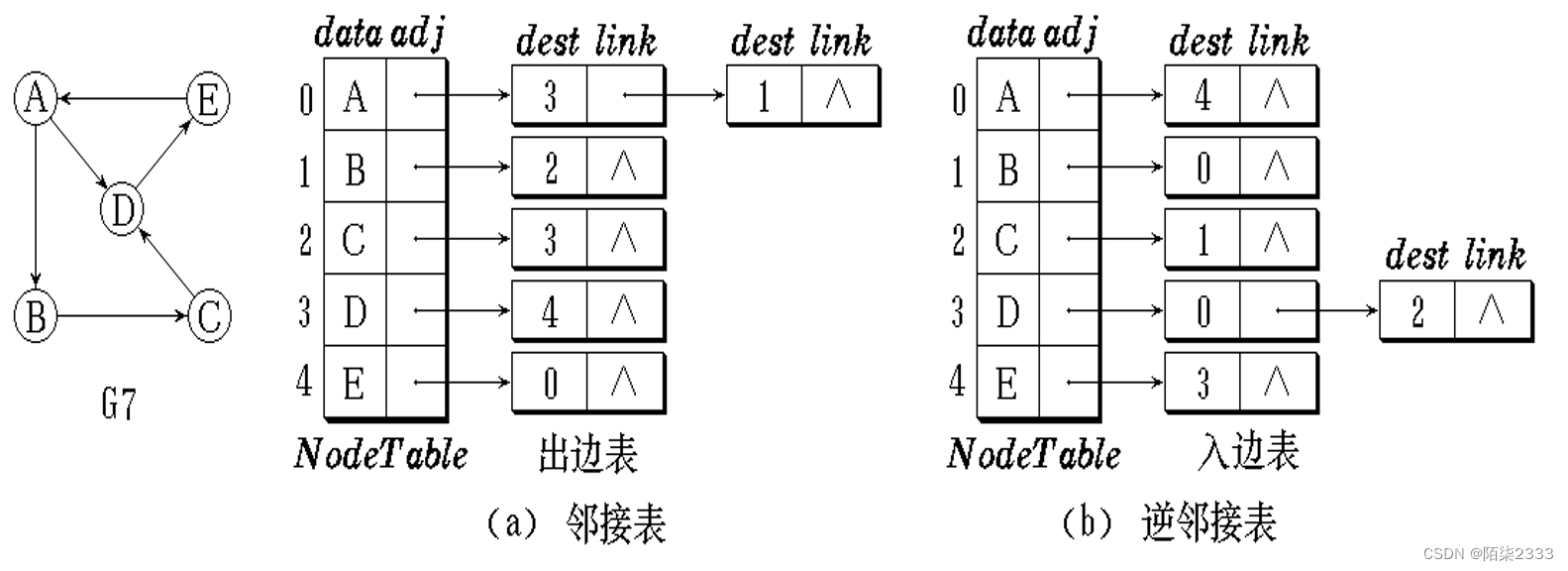
在有向图的邻接表中，第 i 个链表中结点的个数是顶点Vi的出度。

在有向图的逆邻接表中，第 i 个链表中结点的个数是顶点Vi 的入度。

带权有向图：

3.十字链表      

十字链表Orthogonal List)是有向图的另一种链式存储结构。 我们也可以把它看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。 有向图中的每一条弧对应十字链表中的一个弧结点， 同时有向图中的每个顶点在十字链表中对应有一个结点， 叫做顶点结点。这两类结点结构如图所示。

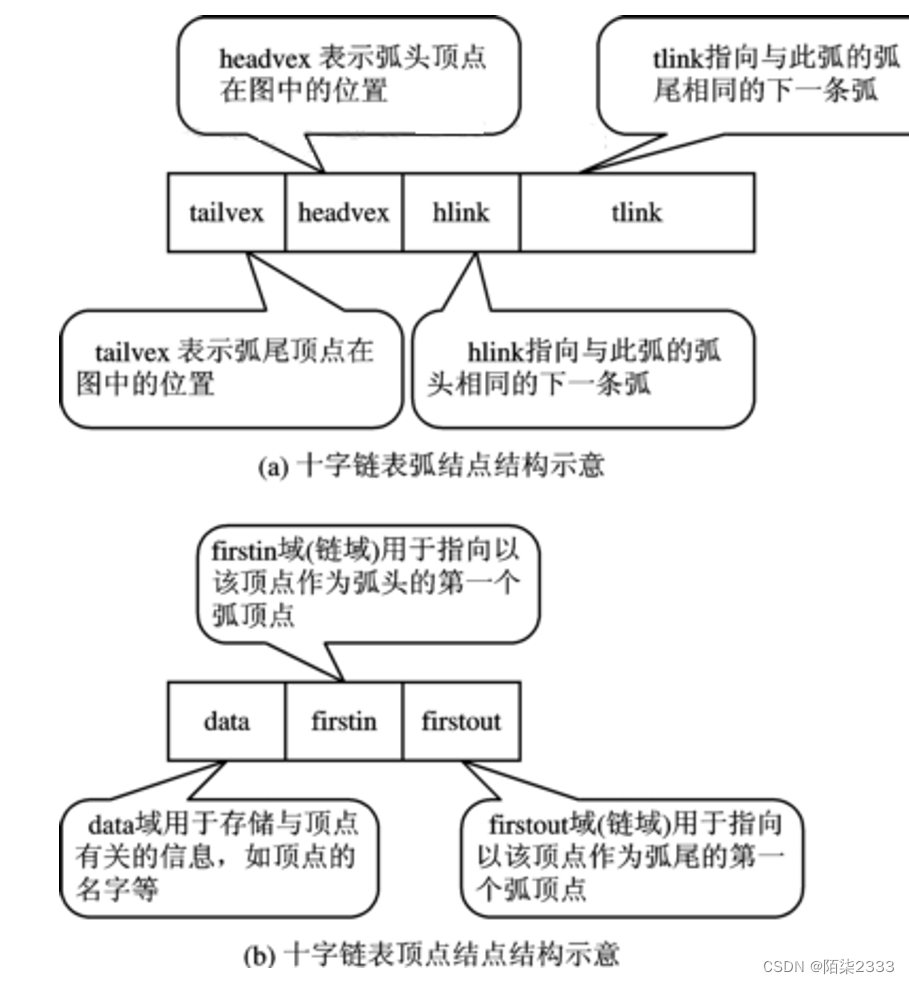
#define  MAX-VERTEX-NUM   10               /*最多顶点个数*/
typedef  enum{DG,  DN,  UDG,  UDN}  GraphKind;    /*图的种类*/ typedef  struct  ArcNode {int    tailvex,   headvex;   struct  ArcNode  *hlink,   *tlink;      } ArcNode; typedef struct VertexNode{VertexData   data;      /*顶点信息*/ArcNode    *firstin,   *firstout;     }VertexNode; typedef struct{VertexNode   vertex［MAX-VERTEX-NUM］;     int   vexnum,   arcnum;     /*图的顶点数和弧数*/ GraphKind   kind;                 /*图的种类*/} OrthList;         /*图的十字链表表示法(Orthogonal List)*/ 

//建立十字链表
void  CrtOrthList（OrthList g）
/*从终端输入n个顶点的信息和e条弧的信息， 以建立一个有向图的十字链表*/
{scanf(″%d, %d″, &n, &e);  /*从键盘输入图的顶点个数和弧的个数*/ for (i=0; i<n; i++) {scanf(″%c″, g.vertex［i］.data）； g.vertex［i］ .firstin=NULL； g.vertex［i］ .firstout=NULL； } for (k=0; k<e; k++) {scanf(″%c, %c″, &vt, &vh); i=LocateVertex（g， vt）； j = LocateVertex（g，vh）； p=alloc(sizeof(ArcNode)); p->tailvex=i； p->headvex=j； p->tlink = g.vertex［i］.firstout； g.vertex［i］.firstout =p； p->hlink = g.vertex［j］.firstin； g.vertex［j］.firstin =p； }}/* CrtOrthList */ 

4.邻接多重表

邻接多重表(Adjacency Multi-list)是无向图的另外一种存储结构， 之所以提出邻接多重表这种存储结构是因为它能够提供更为方便的边处理信息。 在无向图的邻接表表示法中， 每一条边（vi， vj）在邻接表中都对应着两个结点， 它们分别在第i个边链表i和第j个边链表中。 这给图的某些边操作带来不便， 如检测某条边是否被访问过， 则需要同时找到表示该条边的两个结点， 而这两个结点又分别在两个边链表中。 邻接多重表是指将图中关于一条边的信息用一个结 点来表示， 图中的每一个顶点也对应一个顶点结点。

typedef  struct  EdgeNode { int  mark, ivex, jvex; struct  EdgeNode  *ilink,   *jlink; 
}EdgeNode; 
typedef struct { VertexData  data;  EdgeNode  *firstedge; 
}VertexNode; 
typedef struct{VertexNode  vertex［MAX-VERTEX-NUM］;     int   vexnum,   arcnum;              /*图的顶点数和弧数*/ GraphKind   kind;                        /*图的种类*/
} AdjMultiList;          /*基于图的邻接多重表表示法(Adjacency Multi-list)*/ 

2.图的遍历

图的遍历(Travelling Graph):从图中某一个顶点出发，访问图中的其余顶点，使每个顶点被访问一次且仅被访问一次。

方法： 深度优先搜索，广度优先搜索

设访问标志数组visited[]：用于标示图中每个顶点是否被访问过，它的初始值为0(“假”)，表示顶点均未被访问；一旦访问过顶点vi，则置访问标志数组中的visited［i］为1(“真”)，以表示该顶点已访问。

1.深度优先搜索        

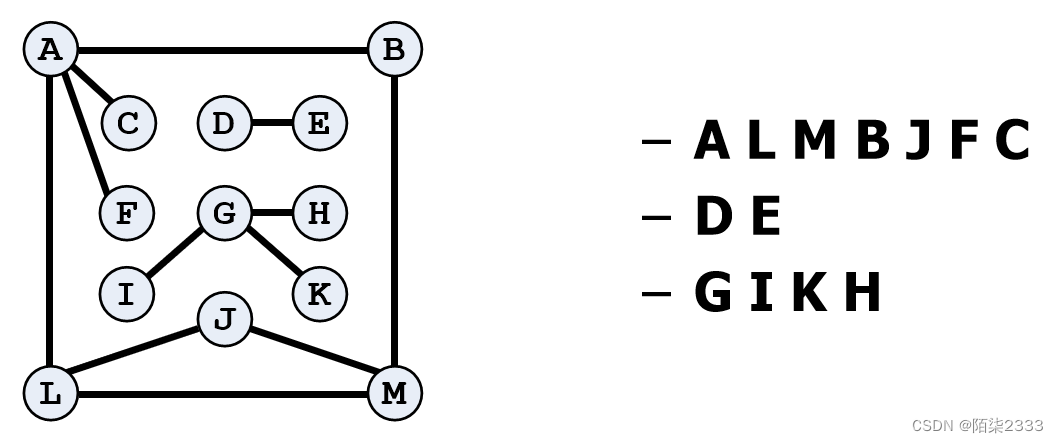
深度优先搜索（Depth-First Search）是指按照深度方向搜索，它类似于树的先根遍历，是树的先根遍历的推广。        

深度优先搜索连通子图的基本思想是：      

（1） 从图中某个顶点v0出发，首先访问v0。      

（2）找出刚访问过的顶点vi的第一个未被访问的邻接点， 然后访问该顶点。以该顶点为新顶点，重复本步骤，直到当前的顶点没有未被访问的邻接点为止。      

（3）返回前一个访问过的且仍有未被访问的邻接点的顶点， 找出并访问该顶点的下一个未被访问的邻接点，然后执行步骤(2)。

采用递归的形式说明，则深度优先搜索连通子图的基本思想可表示为：    

（1） 访问出发点v0。      

（2）依次以v0的未被访问的邻接点为出发点， 深度优先搜索图， 直至图中所有与v0有路径相通的顶点都被访问。        

若此时图中还有顶点未被访问，则另选图中一个未被访问的顶点作为起始点，重复上述深度优先搜索过程，直至图中所有顶点均被访问过为止。        

void DFSTraverseAL(ALGraph *G)	/*算法6-3 */
{	int i;for (i=0; i<G->n; i++)visited[i] = FALSE;    /*标志向量初始化*/for (i=0; i<G->n; i++) 	/*vi未访问过，从vi开始DFS搜索*/if (!visited[i]) DFSAL(G, i);          		
}

void DFSAL(ALGraph *G, int i)		/*算法6-4*/
{	EdgeNode *p;printf("visit vertex:V%c\n", G->adjlist[i].vertex);  /*访问顶点vi*/visited[i]=TRUE;                     /*标记vi已访问*/p=G->adjlist[i].firstedge;       /*取vi边表的头指针*/while(p)                            	  /*依次搜索vi的邻接点vj */{	if (!visited[p->adjvex])    /*若vj尚未访问，则以vj为出发点向纵深搜索*/DFSAL(G,p->adjvex);p=p->next;                 /*找vi的下一个邻接点/}
}

设无向图G有n个顶点、e条边，由于对邻接表中的每个顶点最多检测一次，共有2e个表结点，故完成搜索的时间复杂度为O(n+e)。

2.广度优先搜索

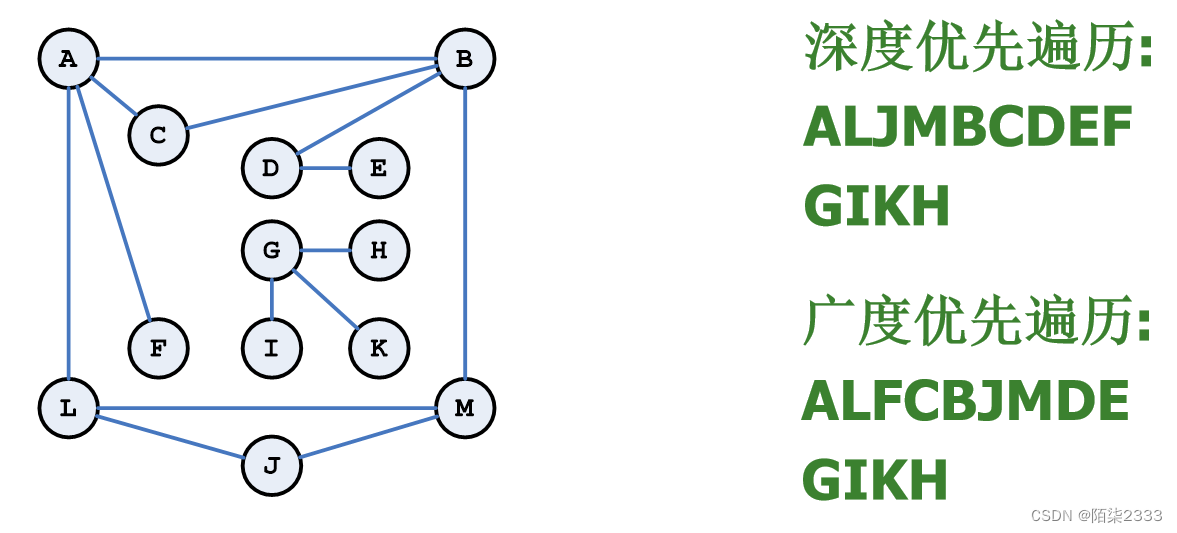
 广度优先搜索（Breadth-First Search）是指照广度方向搜索，它类似于树的层次遍历，是树的按层次遍历的推广。广度优先搜索的基本思想是：    

（1） 从图中某个顶点v0出发，首先访问v0 。    

（2） 依次访问v0的各个未被访问的邻接点。    

（3）分别从这些邻接点（端结点）出发，依次访问它们的各个未被访问的邻接点（新的端结点）。访问时应保证：如果vi和vk为当前端结点，vi在vk之前被访问， 则vi的所有未被访问的邻接点应在vk的所有未被访问的邻接点之前访问。重复（3）， 直到所有端结点均没有未被访问的邻接点为止。 

广度优先遍历——仿树的层次遍历过程

访问顶点v

依次访问顶点v的各个未被访问的邻接点

分别从这些邻接点出发，依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于”后被访问的顶点的邻接点”被访问

若此时图中尚有顶点未被访问，则任选其一为起点，重复，直至图中所有顶点都被访问到

注意对比树的层序遍历

广度优先搜索在搜索访问一层时，需要记住已被访问的顶点，以便在访问下层顶点时，从已被访问的顶点出发搜索访问其邻接点。所以在广度优先搜索中需要设置一个队列Queue，使已被访问的顶点顺序由队尾进入队列。在搜索访问下层顶点时，先从队首取出一个已被访问的上层顶点，再从该顶点出发搜索访问它的各个邻接点。

void BFSTraverseAL(MGraph *G)
{	int i;for (i=0; i<G->n; i++)visited[i] = FALSE;            /*标志向量初始化*/for (i=0; i<G->n; i++)if (!visited[i]) 	     /* vi未访问过，从vi开始BFS搜索*/BFSM(G, i);
}

void BFSM(MGraph *G,int k)
{   int i, j;     CirQueue *Q;       InitQueue(Q);printf("visit vertex:V%c\n", G->vexs[k]);               /*访问原点vk*/visited[k] = TRUE;       EnQueue(Q, k);                   /*原点vk入队列*/while (!QueueEmpty(Q)){	i = DeQueue(Q);                      	/*vi出队列*/for (j=0; j<G->n; j++)                   	/*依次搜索vi的邻接点vj*/if (G->edges[i][j]==1 && !visited[j]) 		/*若vj未访问*/{	printf("visit vertex:V%c\n", G->vexs[j]); 	/*访问vj */visited[j] = TRUE;EnQueue(Q, j);            	/*访问过的vj入队列*/}}
}

算法的时间复杂度为O(n2)。如果采用邻接表作为存储结构，所需时间复杂度为O(n+e)。

例题：

求距离顶点v0的路径长度为k的所有顶点。 已知无向图g， 设计算法求距离顶点v0的最短路径长度为K的所有顶点， 要求尽可能节省时间。 

void bfsKLevel(Graph  g,  int  v0,  int  K)
{ InitQueue(Q1); 	　/* Q1是存放已访问顶点的队列*/ InitQueue(Q2);              /* Q2是存放已访问顶点层号的队列 */ for (i=0; i < g .vexnum; i++)  visited［i］=FALSE;         /* 初始化访问标志数组 */visited［v0］=TRUE;  Level=1; EnterQueue(Q1, v0); EnterQueue(Q2, Level); while (! IsEmpty(Q1) && Level<K+1){v=DeleteQueue(Q1);         　 /* 取出已访问的顶点号 */ Level=DeleteQueue(Q2);       /* 取出已访问顶点的层号 */  w=FirstAdjVertex(g, v);         /* 找第一个邻接点 */while (w!=-1) {   if (! visited［w］)  {     if  (Level==K)  printf(″%d″, w);    /* 输出符合条件的结点 */   visited［w］=TRUE;     EnterQueue(Q1,  w);     EnterQueue(Q2,  Level+1);      }  w=NextAdjVertex(g, v, w);         /* 找下一个邻接点 */  }}}