文章目录
- 基本概念
- 凸集
- 凸函数
- 下一篇
基本概念
- 可行点(可行解):在规划问题中,满足约束条件的点
- 可行集或可行域:全体可行点组成的集合
- 无约束问题:如果一个问题的可行集是整个空间。
分为三种情况:
- S = ∅ , 则称该问题无解或不可行 S = \emptyset, 则称该问题无解或不可行 S=∅,则称该问题无解或不可行
- S ≠ ∅ , 但是目标函数在 S 上无界 S \not = \emptyset, 但是目标函数在S上无界 S=∅,但是目标函数在S上无界
- S ≠ ∅ 且目标函数有限的最优解,则称问题有最优解 S \not = \emptyset 且目标函数有限的最优解,则称问题有最优解 S=∅且目标函数有限的最优解,则称问题有最优解
符号问题:
x ∈ R n x\in R^n x∈Rn表示 x x x 是向量
x ∈ R x \in R x∈R表示 x x x 是实数
黑体的是向量
没有加粗的是数
凸集
凸集定义:设S为n维欧式空间 R n R^n Rn中的一个集合。若对任意两点 x ( 1 ) , x ( 2 ) ∈ S x^{(1)}, x^{(2)} \in S x(1),x(2)∈S及每个实数 λ ∈ [ 0 , 1 ] \lambda \in [0, 1] λ∈[0,1] 有
λ ∗ x ( 1 ) + ( 1 − λ ) ∗ x ( 2 ) ∈ S \lambda * x^{(1)} + (1 - \lambda) * x^{(2)} \in S λ∗x(1)+(1−λ)∗x(2)∈S
则称S为凸集。 λ ∗ x ( 1 ) + ( 1 − λ ) ∗ x ( 2 ) \lambda * x^{(1)} + (1 - \lambda) * x^{(2)} λ∗x(1)+(1−λ)∗x(2)称为 x ( 1 ) x^{(1)} x(1)和 x ( 2 ) x^{(2)} x(2)的凸组合。
凸组合定义:给定m个向量, x 1 , x 2 , . . . , x m ∈ R n x^1, x^2,...,x^m \in R^n x1,x2,...,xm∈Rn, 以及满足 ∑ λ i = 1 \sum{\lambda_i = 1} ∑λi=1的非负实数 λ i ∈ R \lambda_i \in R λi∈R, 称向量 λ 1 x 1 + λ 2 x 2 + . . . + λ m x m \lambda_1 x^1 + \lambda_2 x^2 + ... + \lambda_m x^m λ1x1+λ2x2+...+λmxm为 x x x 的凸组合。
根据向量知识凸组合形成的集合图形为两顶点之间的连线
定理:如果S为凸集那么其中具有任意有限元素的凸组合。
凸集性质:
- 凸集放大 α \alpha α倍仍为凸集
- 凸集相交仍为凸集
- 凸集的元素求和仍为凸集
- 凸集的元素相减仍为凸集
凸包定义:凸包,给定一堆点,这堆点的凸包就是包含这些点的最小凸集。
这些点称为单纯形的顶点。
闭包:
- 闭集的闭包就是它本身
- 开集的闭包就是它本身加上它的边界集
凸锥定义:设有集合 C ⊂ R n C\subset R^n C⊂Rn, 若对每一点 x ∈ C x \in C x∈C,当 λ \lambda λ 取任何非负数时,都有 λ x ∈ C \lambda x \in C λx∈C, 称C为锥,如果C为凸集,则称C为凸锥。
从零点到x延长线上的点仍在集合C中

凸锥组合:
{ ∑ λ i α ( i ) ∣ λ i > = 0 , i = 1 , 2... k } \{\sum{\lambda_i \alpha^{(i)}} | \lambda_i >= 0, i = 1, 2 ...k\} {∑λiα(i)∣λi>=0,i=1,2...k}
多面集:由有限个半空间的交组成的集合为多面集
{ x ∣ A x < = b } \{ x | Ax <= b\} {x∣Ax<=b}
常见于线性规划的可行域
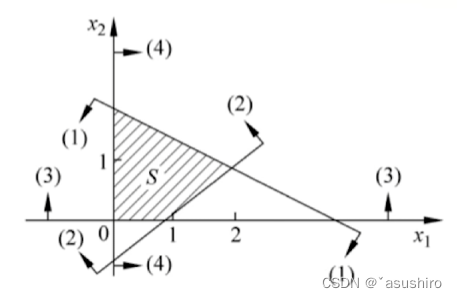
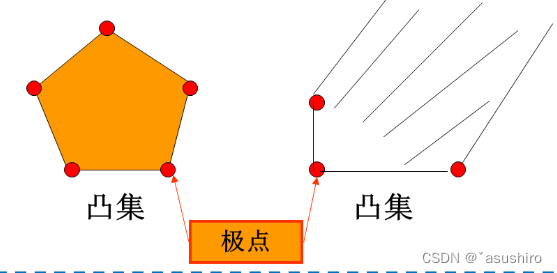
极点定义:若S为非空凸集, x ∈ S x \in S x∈S, 若由 x = λ x ( 1 ) + ( 1 − λ ) x ( 2 ) x = \lambda x^{(1)} + (1 - \lambda) x^{(2)} x=λx(1)+(1−λ)x(2)必有 x = x ( 1 ) = x ( 2 ) x = x^{(1)} = x^{(2)} x=x(1)=x(2),则x是S的极点。
任何有界凸集中任意点都可以表示成极点的凸组合。 但是极点不能被其他两点表示。
圆的边缘上的点都是极点。
凸集的方向:如果凸集中的一个点引出一条射线,这条射线上所有的点仍在凸集内,则称这个射线的方向为回收方向(方向),而这所有的方向全部形成的尖锥称为凸集的回收锥。

方向:设S为 R n R^n Rn中的闭凸集,d为非零向量,如果对S中的每一个 x x x ,都有射线 { x + λ d ∣ λ > = 0 } ⊂ S \{ x + \lambda d | \lambda >= 0\} \subset S {x+λd∣λ>=0}⊂S则称向量 d d d 为S的方向。
极方向:如果方向 d d d 无法由其他两个方向的凸组合得到,那么方向d就是凸锥的极方向。(凸锥组合就是两个方向中夹角的一个方向,向量加法)
性质定理
-
表示定理:

即多面集可以由极点的凸组合和极方向的凸锥组合全部表示出来 -
凸集分离定理
设 S 1 S_1 S1和 S 2 S_2 S2是 R n R^n Rn中两个非空集合, H = { x ∣ p T x = α } H= \{ x | p^T x = \alpha\} H={x∣pTx=α}为超平面, 如果对 ∀ x ∈ S 1 \forall x \in S_1 ∀x∈S1, 都有 p T x > = α p^T x >= \alpha pTx>=α, 对于每个 x ∈ S 2 x \in S_2 x∈S2, 都有 p T x < = α p^T x<= \alpha pTx<=α(或者相反),则称超平面 H H H分离集合 S 1 S_1 S1和 S 2 S_2 S2。

-
闭凸集的一个性质
设 S S S 为 R n R^n Rn中的闭凸集, y ∉ S y\not \in S y∈S,则存在唯一的点 x ^ ∈ S \hat{x} \in S x^∈S, 使得
∣ ∣ y − x ^ ∣ ∣ = i n f x ∈ S ∣ ∣ y − x ∣ ∣ ||y- \hat{x}|| = inf_{x\in S}||y - x|| ∣∣y−x^∣∣=infx∈S∣∣y−x∣∣
可以找到唯一的一个点使得y到集合S的距离是最小的,且只有到这个点的距离是最小距离

-
点与凸集分离定理
设 S S S是 R n R^n Rn中的非空闭凸集, y ∉ S y \not \in S y∈S, 则存在非零向量 p p p及数 ξ > 0 \xi > 0 ξ>0, 使得对每一个点 x ∈ S x \in S x∈S, 成立 p T y > = ξ + p T x p^T y >= \xi + p^T x pTy>=ξ+pTx

可以在点和凸集中间找到一个超平面
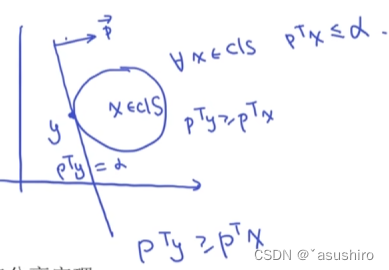
考虑边界的情况 -
凸集分离定理
设 S 1 S_1 S1 和 S 2 S_2 S2是 R n R^n Rn的两个非空凸集, S 1 ∩ S 2 = ∅ S_1 \cap S_2 = \emptyset S1∩S2=∅, 则存在非零向量 p p p, 使得
i n f { p T ∣ x ∈ S 1 } > = s u p { p T x ∣ x ∈ S 2 } inf \{p^T | x \in S_1 \} >= sup \{ p^T x | x \in S_2\} inf{pT∣x∈S1}>=sup{pTx∣x∈S2}两个交集非空的凸集一定能找到一个超平面将他们分离
-
择一定理
不等式组解的充分必要条件- Farkas定理
设A为m x n矩阵, c为n维向量,则 A x < = 0 , c T x > 0 Ax <= 0, c^T x > 0 Ax<=0,cTx>0有解的充分必要条件是 A T y = c , y > = 0 A^T y = c, y >= 0 ATy=c,y>=0无解。 - Gordan引理
设A为m x n矩阵,那么,Ax < 0 有解的充分条件是不存在非零向量 y >= 0, 使 A T y = 0 A^T y = 0 ATy=0
- Farkas定理
凸函数
凸函数定义:设S是 R n R^n Rn 中的非空凸集, f ( x ) f(x) f(x) 是定义在S上的实函数,如果对于每一对 x 1 , x 2 ∈ S x_1, x_2 \in S x1,x2∈S 及每一个 a a a, 0 < = a < = 1 0 <= a <= 1 0<=a<=1, 都有
f ( a x 1 + ( 1 − a ) x 2 ) < = a f ( x 1 ) + ( 1 − a ) f ( x 2 ) f(ax_1 +(1 - a)x_2) <= af(x_1) + (1 - a)f(x_2) f(ax1+(1−a)x2)<=af(x1)+(1−a)f(x2)
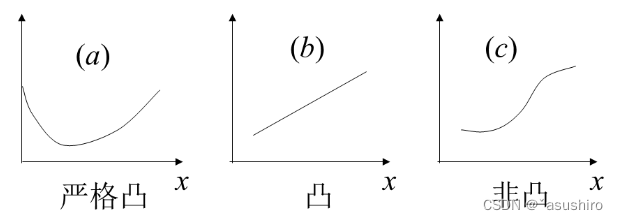
则称函数 f ( x ) f(x) f(x) 为S上的凸函数, 当 < = <= <= 变成 <,则称为严格凸函数。
凸函数性质
- 凸函数的线性组合仍为凸函数
- 截取凸函数连续的一段它的定义域是凸集
- 凸函数的局部极小点是整体极小点

凸函数的判定
一阶充要条件:
设S是 R n R^n Rn 中非空开凸集, f ( x ) f(x) f(x) 是定义在S上的可微函数, 则 f ( x ) f(x) f(x)为图函数的充要条件是对任意两点 x ( 1 ) x^{(1)} x(1), x ( 2 ) ∈ S x^{(2)} \in S x(2)∈S, 有
f ( x ( 2 ) ) − f ( x 1 ) > = ▽ f ( x ( 1 ) ) ( x ( 2 ) − x ( 1 ) ) f(x^{(2)}) - f(x^{1}) >= \bigtriangledown f(x^{(1)})(x^{(2)} - x^{(1)}) f(x(2))−f(x1)>=▽f(x(1))(x(2)−x(1))
将 > = >= >=改为 > > >就是严格凸

f ( x ) f(x) f(x)是凸函数当且仅当任意点处的切线增量不超过函数增量
二阶充要条件:
设 S S S 是 R n R^n Rn 中非空开凸集, f ( x ) f(x) f(x) 是定义在S上的二次可微函数,则 f ( x ) f(x) f(x)为凸函数的充要条件是对任意 x ∈ S x \in S x∈S, f ( x ) f(x) f(x) 在x 处的 Hessian矩阵 ▽ 2 f ( x ) \bigtriangledown^2 f(x) ▽2f(x)是半正定的。
对二次函数,
正定为严格凸函数。
半正定为凸函数。

下一篇
未完待续






vModel双向绑定函数)

)



)






