Leetcode1038. 从二叉搜索树到更大和树(每日一题）

⚽题目：

🏐题目分析：

🏀题目解答：

🥎代码如下：

⚽题目：

给定一个二叉搜索树 root (BST)，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

提醒一下， 二叉搜索树 满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

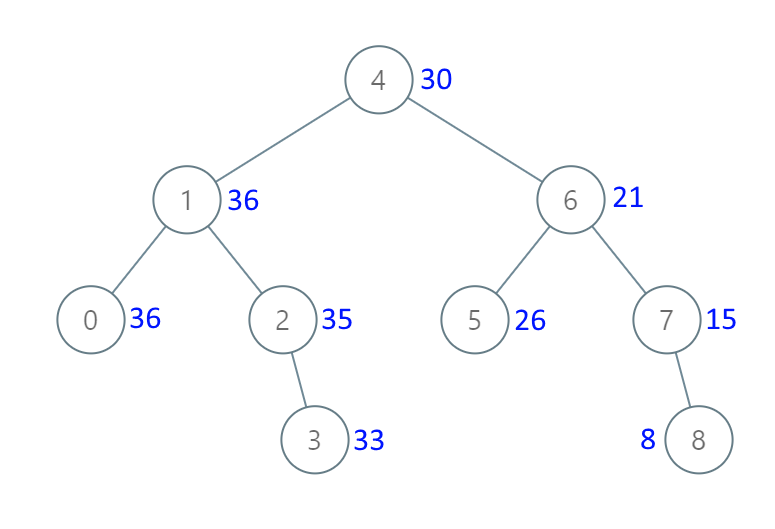
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

提示：

树中的节点数在 [1, 100] 范围内。
0 <= Node.val <= 100
树中的所有值均 不重复 。

🏐题目分析：

1、看到树的问题首先想到递归处理，递归处理的方法首先想到前序、中序、后序三种类型。一般树的问题的解决都是这三种类型的变形！！

2、接下来观察本题树的特征，树的特征观察一定不要整体去看，相反要局部的去看，这与我们递归化为子问题处理有内在逻辑关系。例如本题看这个树的特征，我们就选择根节点去看，思考根节点和其他节点有什么内在关系。

3、做了以上分析，最后我们再根据得到的特征关系去思考如何进行递归，也就是如何将一个大问题分解为子问题去解决。

🏀题目解答：

接下来的题目解答就是根据上面的三个思考方向对问题进行思考解决。

1、本题的递归方法是中序遍历的变形。先处理右子树再处理根节点最后处理左子树。采取这种策略的原因是根节点的值和右子树有关，而左子树的处理和右子树以及根节点都没有关系。

2、局部来看，根节点的值就是其右子树的结点值加上根节点本身的值。而右子树节点的值又是他的右子树节点值加上其本身的值。如此递归往复

3、修改整个树的结点的值可以分解为——>>修改右子树所有结点值、修改整个树根节点值、修改左子树所有结点值。而整个树根节点的值又可以化为：整个树根节点的值=右子树根节点的值+整个树根节点原本的值。根据这个求解公式大家不难发现，整个树根节点的值的修改依赖于右子树结点值的修改。这也就是我们选择中序解决问题的原因。

分析到这里，我想大家也就明白啦~~

🥎代码如下：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int s=0;TreeNode* bstToGst(TreeNode* root) {dfs(root);return root;}void dfs(TreeNode* root){if(root==NULL)return;dfs(root->right);s+=root->val;//这一步s=s+root->val中前面的s可以认为是该结点右子树所有右节点值之和，新的s就是目前root应该是的值root->val=s;dfs(root->left);}
};

创作不易，如果觉得内容不错，收藏一下呗，小猫求求了~