一元三次方程求解
- 题目描述
- 提示
- 输入输出格式
- 输入格式
- 输出格式
- 输入输出样例
- 输入样例
- 输出样例
- 算法分析
- A C 代码
题目描述
有形如: a x 3 + b x 2 + c x + d = 0 ax^3+bx^2+c^x+d=0 ax3+bx2+cx+d=0一元三次方程。给出该方程中各项的系数 ( a a a, b b b, c c c, d d d 均为实数 ),并约定该方程存在三个不同实根 (根的范围在 − 100 -100 −100至 100 100 100之间 ),且根与根之差的绝对值 ≤ 1 ≤1 ≤1。要求由小到大依次在同一行上输出这三个实根。
提示
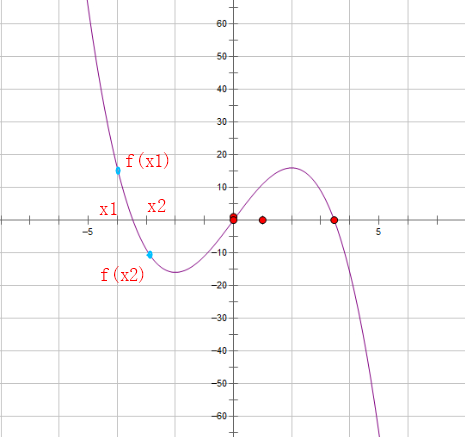
记方程 f ( x ) = 0 f(x)=0 f(x)=0,若存在两个数 x 1 x_1 x1和 x 2 x_2 x2,且 x 1 < x 2 x_1 < x_2 x1<x2, f ( x 1 ) × f ( x 2 ) < 0 f(x_1)×f(x_2)<0 f(x1)×f(x2)<0,则在 ( x 1 , x 2 ) (x_1,x_2) (x1,x2)之间一定有一个根。
输入输出格式
输入格式
输入 a , b , c , d a,b,c,d a,b,c,d
输出格式
三个实根(根与根之间留有空格)
输入输出样例
输入样例
1 -5 -4 20
输出样例
-2.00 2.00 5.00
算法分析
这是一道有趣的解方程题。为了便于求解,设方程 f ( x ) = a x 3 + b x 2 + c x + d = 0 f(x)=ax^3+bx^2+cx+d=0 f(x)=ax3+bx2+cx+d=0,设根的值域( − 100 -100 −100至 100 100 100之间)中有 x x x, 其左右两边相距 0.0005 0.0005 0.0005的地方有 x 1 x_1 x1和 x 2 x_2 x2两个数,即 x 1 = x − 0.0005 x_1=x-0.0005 x1=x−0.0005, x 2 = x + 0.0005 x_2=x+0.0005 x2=x+0.0005。 x 1 x_1 x1和 x 2 x_2 x2间的距离( 0.001 0.001 0.001)满足精度要求(精确到小数点后 2 2 2位)。
A C 代码
暴力出奇迹~~
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
int main()
{cin >>a >>b >>c >>d;for(double i=-100;i<=100;i+=0.001){double j=i+0.001;double l=a*i*i*i+b*i*i+c*i+d;double r=a*j*j*j+b*j*j+c*j+d;if(l*r<=0){printf("%.2lf ",(i+j)/2);}}return 0;
}
![P2141 [NOIP2014 普及组] 珠心算测验](http://pic.xiahunao.cn/P2141 [NOIP2014 普及组] 珠心算测验)



配置)


——物联网之Yeelight 3)

: HDMI输入和输出显示1080p视频)

)
:函数进阶)





)
