编译工具:PyCharm
文章目录
- 编译工具:PyCharm
- 决策树算法
- 信息熵
- 信息熵例题计算:
- 信息增益(决策树划分依据之一ID3)
- 信息增益例题计算:
- 信息增益率(决策树划分依据之一C4.5)
- 基尼值和基尼指数(决策树划分依据之一CART)
- 多变量决策树:OC1
- 剪枝
- 决策树算法api案例:泰坦尼克号存活预测
决策树算法
决策树:是一种树形结构,其中每个内部节点表四一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点表示一种分类结果,本质是一颗由多个判断节点组成的树。
信息熵
“信息熵”时度量原本集合程度最常用的一种指标。
1.当系统的有序状态一致时,数据越集中的地方熵值越小,数据越分散的地方熵值越大。
2.当数据量一致时,系统越有序,熵值越低;系统越混乱/分散,熵值越高。
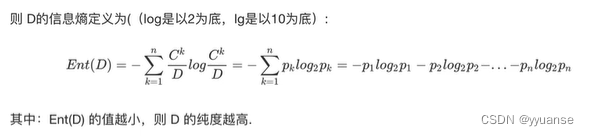
信息熵例题计算:

信息增益(决策树划分依据之一ID3)
信息增益:以某特征划分数据集前后的熵的差值。熵可以表示原本集合的不确定性。熵越大,原本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。

信息增益例题计算:
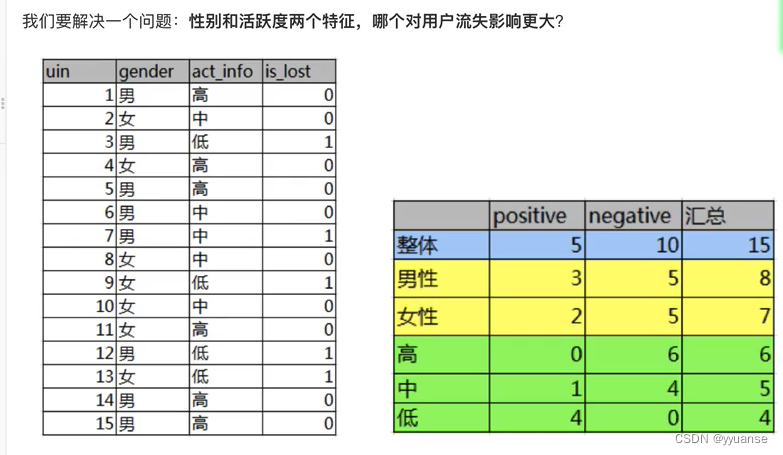
整体流失的信息熵:
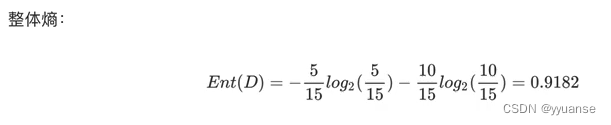
条件信息熵:

信息增益计算:

同样,求解活跃度的信息增益:

信息增益率(决策树划分依据之一C4.5)
信息增益准则对可取值数目较多的属性有所偏好,如在信息增益案例题中,我们计算时忽略了第一列即编号列,实际上信息增益会偏向选择第一列(类别有15种)、第三列(类别有3种)…。但是显然第一列没有计算的必要。
为了减少这种偏好可能带来的不利影响,C4.5决策树算法不直接使用信息增益,而是使用**“增益率”来选择最优划分属性**。
增益率:信息增益(D,a) / 属性a的"固有值"

对信息增益的案例进行增益率的计算:

https://www.bilibili.com/video/BV1pf4y1y7kw/?p=106&spm_id_from=pageDriver&vd_source=3918c4e379f5f99c5ae95581d2cc8cec
基尼值和基尼指数(决策树划分依据之一CART)
基尼值Gini(D):从数据集D中随机抽取两个样本,器类别标记不一致的概率。所以Gini(D)值越小,数据集D的纯度越高。
基尼值:
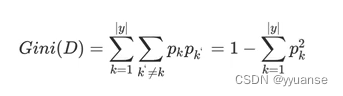
基尼指数:
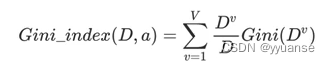
多变量决策树:OC1
ID3、C4.5、CART在特征选择的时候都是选择一个最优的特征来分类决策,但是不应该只由某一个特征进行决定,应该由一组特征决定,OC1就是这样的。
剪枝
剪枝时决策树学习算法中对付“过拟合”的主要手段。
剪枝分为预剪枝和后剪枝
决策树算法api案例:泰坦尼克号存活预测
数据集:https://hbiostat.org/data/repo/titanic.txt
# 决策树算法api
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split # 进行数据集划分
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier# 读取数据
# titan = pd.read_csv("https://hbiostat.org/data/repo/titanic.txt")
titan = pd.read_csv("./data/titanic.csv")
print(titan.describe())# 获取样本和目标值
# 这里取pclass社会等级、age年龄、sex性别作为特征值
# 取survived存活为目标值
x = titan[["pclass","age","sex"]]
y = titan["survived"]# 缺失值处理:对age为空的用平均值替换
x['age'].fillna(value=titan["age"].mean(),inplace=True)
print(x.head())# 数据集划分
x_train,x_test,y_train,y_test = train_test_split(x,y,random_state=22,test_size=0.2)
# 特征抽取(字典特征提取)
x_train = x_train.to_dict(orient="records")
x_test = x_test.to_dict(orient="records")
tranfer = DictVectorizer()
x_train = tranfer.fit_transform(x_train)
x_test = tranfer.fit_transform(x_test)# 模型训练(决策树)
# 在实例化的时候可以添加 max_depth 来提高评估效率score
estimator = DecisionTreeClassifier()
estimator.fit(x_train,y_train)# 模型评估
y_pre = estimator.predict(x_test)
print(y_pre)
print(estimator.score(x_test,y_test))# 决策树可视化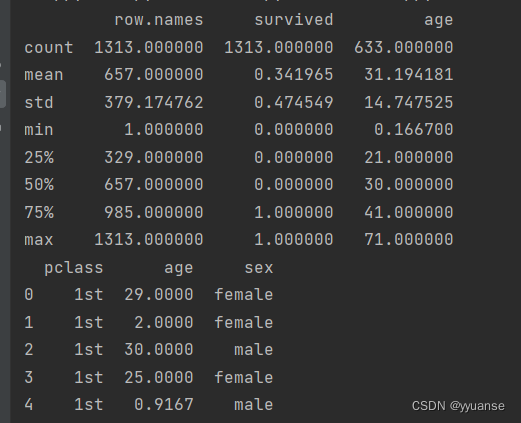


)
应用开发——管理组件状态)
![合并两个有序链表[简单]](http://pic.xiahunao.cn/合并两个有序链表[简单])





)



简介)
)




)