文章目录
- 引言
- 取负运算的奥秘
- 源码探索
- 分析与解读
- 浮点数运算的精细差异
- 源码分析
- 精度损失与隐式类型转换
- 精度和除零运算探究
- float类型和double类型的精度各是多少(即十进制有效位的位数)?
- 在你的机器上,“负数开方”是如何处理的(如“-8.0/0”、“sqrt(-4.0)”的运算结果)?
- 在你的机器上,整数除0和浮点数除0的运行结果各是什么?为什么会有不同的运行结果?,并将“-6.0/0”和“-6/0”的运行结果进行比较。
- 结语
引言
在编程中,理解各种数据类型的运算规则是至关重要的。本文将通过几个示例,深入探讨C语言中整数和浮点数的取负运算、浮点数的精度问题以及除零运算的处理机制。
取负运算的奥秘
源码探索
分析以下简单的C程序:
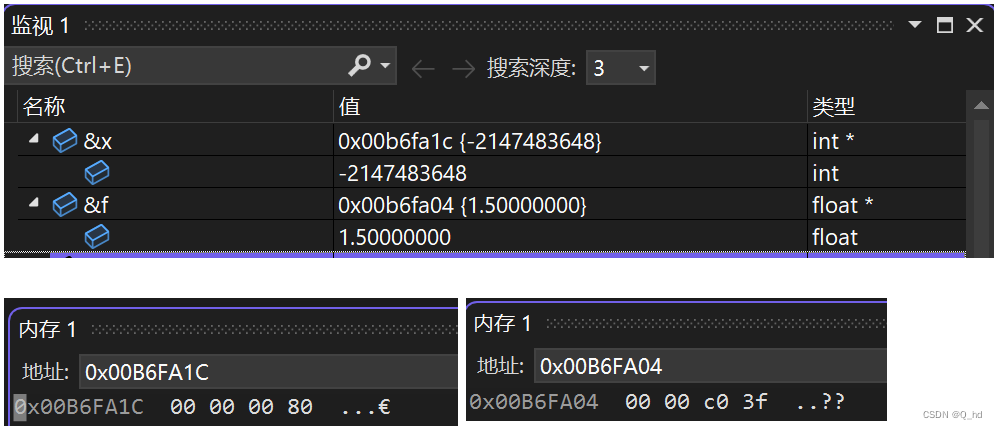
int main()
{int x = -2147483648;int y = 3;float f = 1.5;printf("%d\n", -x > y);printf("%f\n", -f);return 0;
}
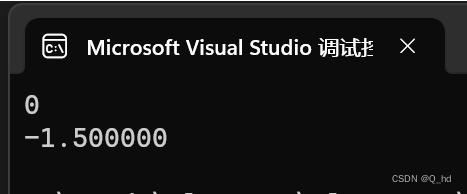
分析与解读
-
当我们对整数
x取负时,由于它已经是32位整数的最小可能值,其补码表示无法再表示一个更大的正数,因此-x仍然等于-2147483648。这导致-x > y的判断为假,因此第一个printf输出为0。 -
另一方面,浮点数
f的取负运算简单明了,结果自然就是-1.5。因此,第二个printf输出-1.500000。
浮点数运算的精细差异
源码分析
接下来,我们看一个涉及浮点数运算的程序:
#include <stdio.h>
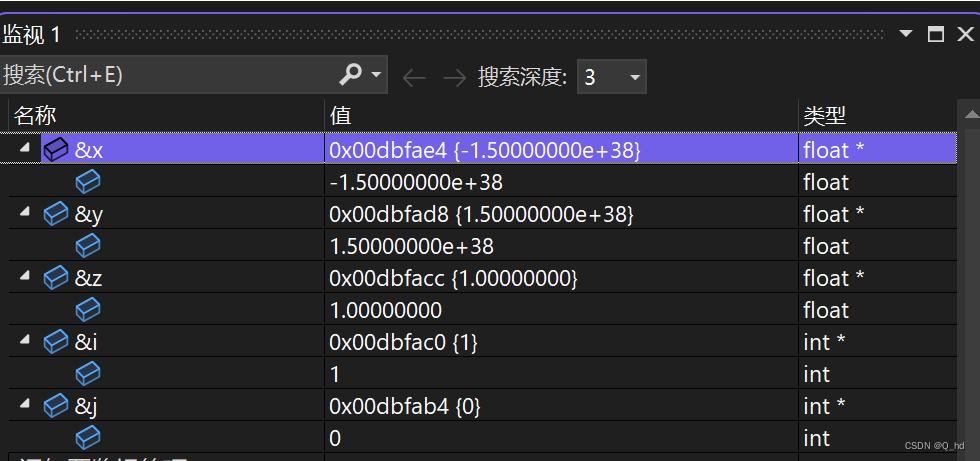
int main()
{float x = -1.5e38;float y = 1.5e38;float z = 1.0;int i = (x + y) + z;int j = x + (y + z);printf("%d\n", i == j);return 0;
}

精度损失与隐式类型转换
-
在上述代码中,我们试图通过不同的运算顺序来比较结果是否相同。然而,由于浮点数的精度限制和整数类型的截断行为,
i和j得到的结果很可能不同,因此输出为0(false)。这个例子清晰地展示了浮点数运算中的精度损失和隐式类型转换可能导致的意外结果。 -
在表达式
(x + y) + z中,x和y是浮点数,而 z 是浮点数转换为整数后的结果。根据C语言的运算规则,当一个浮点数和一个整数进行运算时,整数会被自动转换为浮点数。因此,(x + y)的结果是一个浮点数,再加上z后得到的结果也是一个浮点数。然而,由于i是整型变量,这个浮点数会被截断成整数并赋值给i。
类似地,在表达式x + (y + z)中,y和z是浮点数,而x是一个负浮点数。同样根据C语言的运算规则,负浮点数和浮点数进行运算时,会进行隐式类型转换,使结果仍为浮点数。因此,(y + z)的结果是一个浮点数,再加上x后得到的结果也是一个浮点数。然而,由于j是整型变量,这个浮点数会被截断成整数并赋值给j。 -
如果想要避免隐式类型转换,可以显式地进行类型转换操作,将浮点数转换为整型。例如,可以使用
int(i)或int(j)来将浮点数转换为整型。这样可以确保进行精确的整数比较
精度和除零运算探究
float类型和double类型的精度各是多少(即十进制有效位的位数)?
#include <stdio.h>
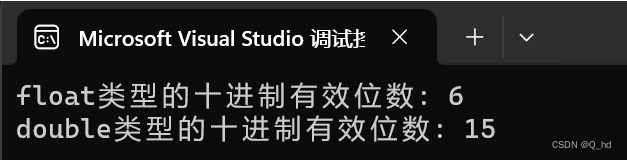
#include <float.h>int main() {printf("float类型的十进制有效位数: %d\n", FLT_DIG);printf("double类型的十进制有效位数: %d\n", DBL_DIG);return 0;
}
在C语言中,可以使用float.h头文件中定义的常量来获取float和double类型的精度信息。具体而言,FLT_DIG和DBL_DIG分别表示float和double类型的十进制有效位数。
这段代码将打印出float和double类型的十进制有效位数。在大多数系统上,你会看到类似以下的输出:
float类型的十进制有效位数: 6
double类型的十进制有效位数: 15
这样就直接获取了float和double类型的十进制有效位数,而无需手动计算。
在你的机器上,“负数开方”是如何处理的(如“-8.0/0”、“sqrt(-4.0)”的运算结果)?
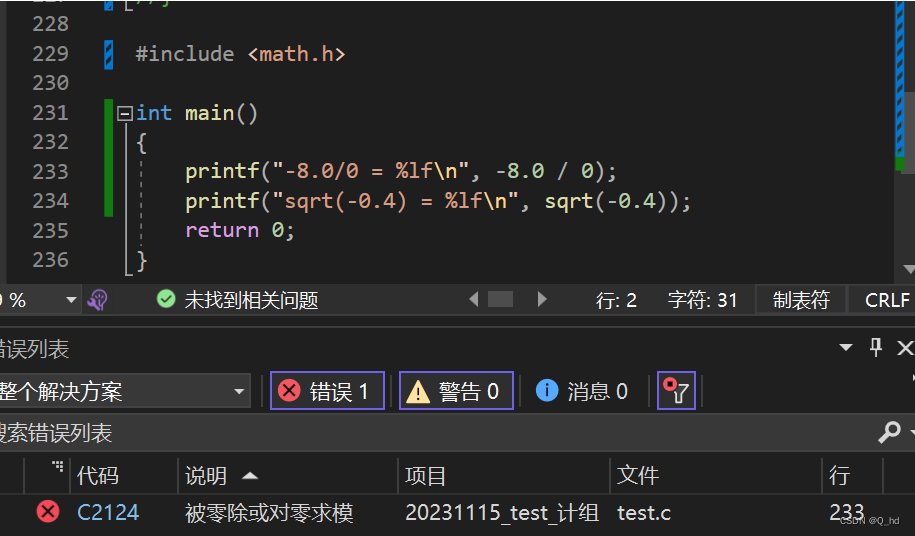
- 当进行表达式
-8.0/0进行计算时,结果会被认为是负无穷大(-∞)。这是因为除以零是一个非法的操作,C语言规定将其视为一种特殊情况,结果被定义为负无穷大或正无穷大。
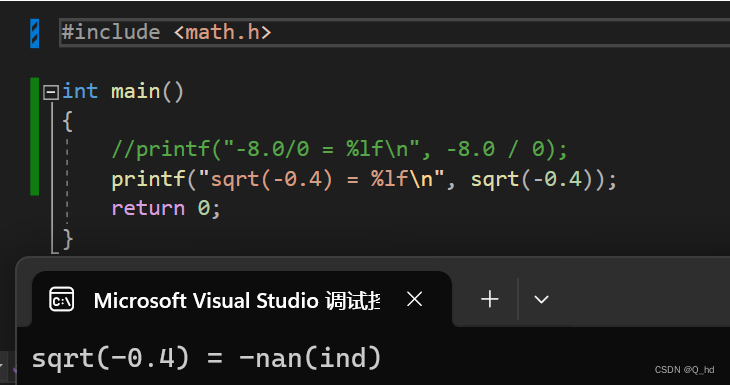
- 当进行表达式
sqrt(-4.0)进行计算时,结果会被认为是一个特殊值NaN(Not a Number),表示无效的操作。负数的平方根是一个虚数,在实数域中没有定义。
在你的机器上,整数除0和浮点数除0的运行结果各是什么?为什么会有不同的运行结果?,并将“-6.0/0”和“-6/0”的运行结果进行比较。
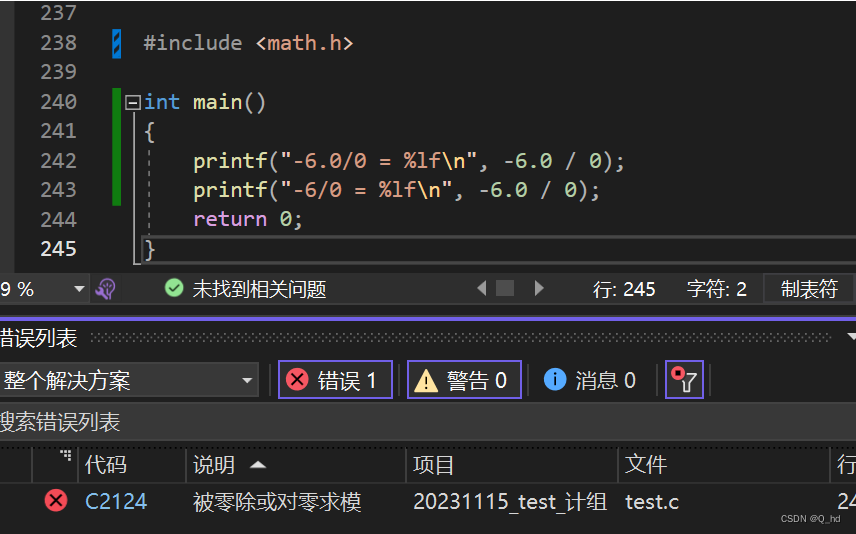
在VS中,错误C2124表示发生了除以零或求模运算中的被零除的情况。这个错误通常出现在编译时,是因为代码中存在了除以零或对零求模的操作,这是一种不合法的操作。
这个错误会阻止程序的继续编译,因为除以零是一种未定义的行为,违反了数学和计算机的基本规则。
要解决这个错误,你需要检查代码中是否存在除以零或对零求模的操作,并确保避免这种情况的发生。可以通过添加适当的条件判断来避免除以零或对零求模,在进行除法或求模运算之前检查除数是否为零。
例如,可以使用条件语句来避免除以零的情况:
if(b != 0) {result = a / b; // 在除数不为零时执行除法运算
}
else{// 处理除数为零的情况,例如输出错误信息或采取其他操作printf("除数不能为零\n");
}
结语
通过本文的分析,我们了解了C语言中数学运算和类型转换的一些关键细节。从取负运算到浮点数的精度,再到除零的处理,每个概念都对编写可靠和高效的代码至关重要。希望这篇文章能帮助你在未来的编程实践中避免一些常见的陷阱。






)




)







)