试题传送门：831. KMP字符串 

给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模式串 P 在字符串 S 中多次作为子串出现。

求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式

第一行输入整数 N，表示字符串 P 的长度。

第二行输入字符串 P。

第三行输入整数 M，表示字符串 S 的长度。

第四行输入字符串 S。

输出格式

共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围

1≤N≤1e5
1≤M≤1e6

输入样例：

3
aba
5
ababa

输出样例：

0 2

试题解析：

题意解释：

在一个字符串S中，寻找字串P，输出P在S中对应的下标。

关于KMP算法：

首先，介绍一下KMP算法与暴力匹配算法的区别。

• 当我们要进行类似本题的字符串匹配操作时，如果使用暴力匹配做法，将P的第一个元素从S的第一个元素开始匹配，如果匹配失败，则将P的第一个元素从S的第二个元素开始匹配，依次类推，这样花费的时间是很长的，时间复杂度为O(M*N)。
• 我们怎么通过一种方式，来进行更快的匹配呢？
  已知每一次匹配失败，p串就移动到s串的下一位开始匹配，那么我们是否可以找到相同的前缀和后缀，选择最长的一端开始匹配呢？
• 前缀：指除了最后一个字符以外，一个字符串的全部头部组合。
  后缀：指除了第一个字符以外，一个字符串的所有尾部组合。
  下面来举个例子：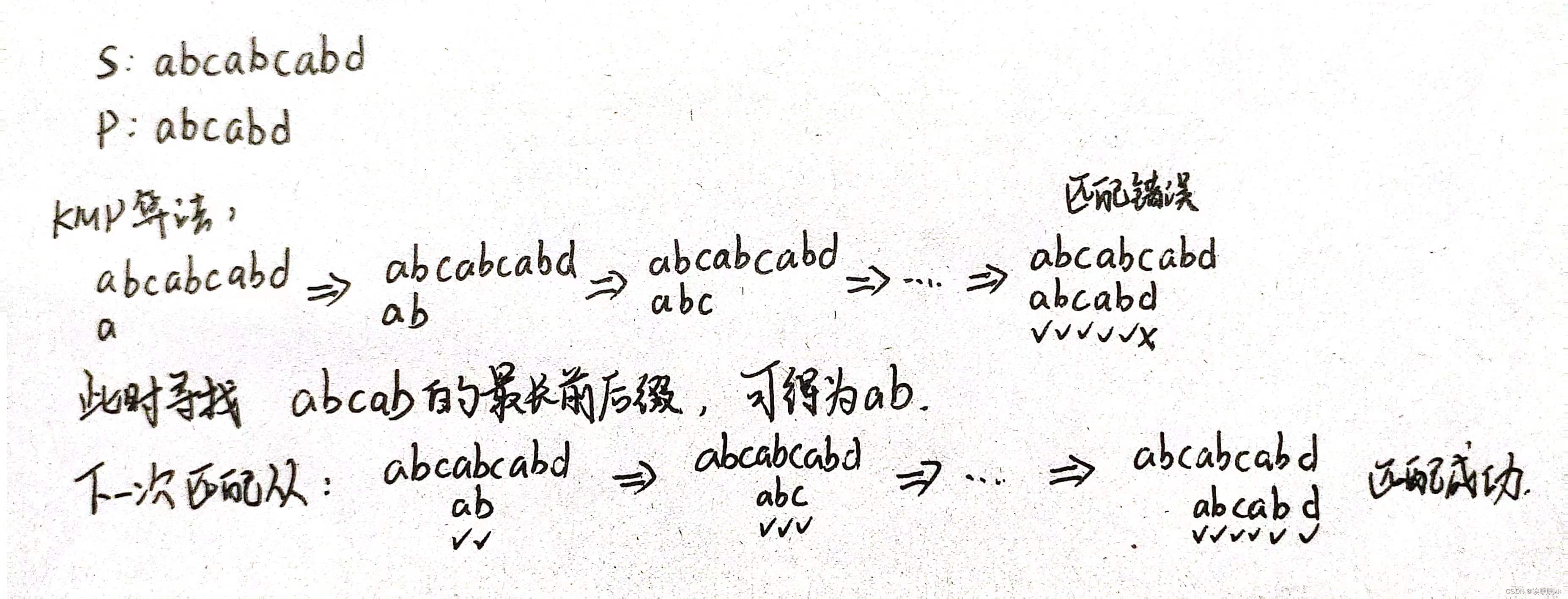
  
  当我们在匹配失败时，可以通过寻找最长前后缀的方式，更新p在s的下一次查找下标，以达到更快的速度。
• next数组（本题为ne数组）的作用便是记录下在某一下标下，p[1...j]串中前后缀相同的最大长度，并将长度记录在下标为j的数组中。
  下面举一个例子方便理解：

  P	a	b	c	a	b
  下标j	1	2	3	4	5
  ne[j]	0	0	0	1	2

• 我们如何在代码上求出next数组呢？
  可以通过模板串p进行自我匹配，求出p[1...j]串中前后缀相同的最大长度，并将长度记录在下标为j的数组中。
  在本题中：i表示匹配成功时对应的下标，j表示自我匹配时p数组中的下标。
  注意细节：在计算next数组的值时，当元素个数为1时，ne[1]绝对为0。

  //j表示匹配成功的长度，i表示p数组中的下标
  //因为p数组下标从1开始，ne[1]一定为0，所以i从2开始
  for (int i = 2, j = 0; i <= n; i++) {while (j && p[i] != p[j + 1]) j = ne[j]; //若不匹配，更新j到ne[j]if (p[i] == p[j + 1]) j++; //成功即匹配下一个ne[i] = j; //保存next数组
  }

• 在进行字符串匹配时，其原理与ne数组的求取相似。
  值得注意的一点是：由于ne数组的值已经求完，现在进行的是S串与P串的匹配操作，那我们的S串就应该从第一个元素开始匹配，当j==n则是匹配成功，输出对应下标并进行下一次的匹配，切记，匹配勿忘ne数组！
  匹配代码如下：

  //j表示匹配成功的长度，从长度为0开始匹配
  for (int i = 1, j = 0; i <= m; i++) {while (j && s[i] != p[j + 1]) j = ne[j]; //若不匹配，更新j到ne[j]if (s[i] == p[j + 1]) j++; //成功即匹配下一个if (j == n) {printf("%d ", i - j); //输出对应下标j = ne[j]; //更新j，继续进行匹配}
  }

题解代码：

最后，我们来给出最终的题解代码。

#include<iostream>
using namespace std;
constexpr int N = 100010, M = 1000010;
char p[N], s[M];
int ne[N];
int main() {int n, m;//字符串下标均从1开始cin >> n >> p + 1 >> m >> s + 1;//j表示匹配成功的长度，i表示p数组中的下标//因为p数组下标从1开始，ne[1]一定为0，所以i从2开始for (int i = 2, j = 0; i <= n; i++) {while (j && p[i] != p[j + 1]) j = ne[j]; //若不匹配，更新j到ne[j]if (p[i] == p[j + 1]) j++; //成功即匹配下一个ne[i] = j; //保存next数组}//j表示匹配成功的长度，从长度为0开始匹配for (int i = 1, j = 0; i <= m; i++) {while (j && s[i] != p[j + 1]) j = ne[j]; //若不匹配，更新j到ne[j]if (s[i] == p[j + 1]) j++; //成功即匹配下一个if (j == n) {printf("%d ", i - j); //输出对应下标j = ne[j]; //更新j，继续进行匹配}}return 0;
}