Problem: 124. 二叉树中的最大路径和

题目描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

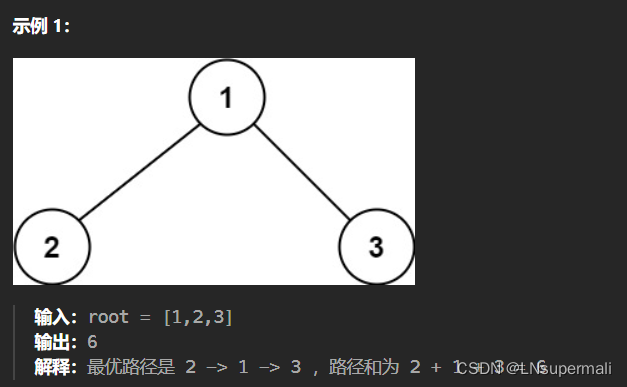
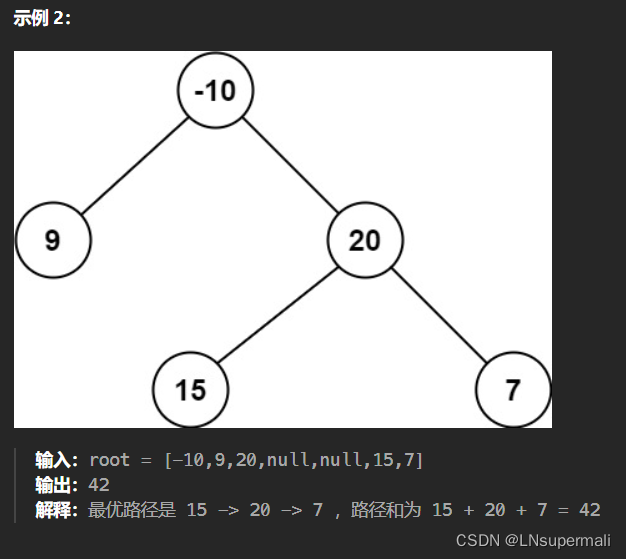
思路

按递归的处理思想将该问题分解成如下最小子问题：

1.分别求取左右子树的最大节点值之和，合并得到整个树的最大节点值之和（每个节点值，我们称其为对最终最大节点值之和的贡献）。
2.具体的分解处理中：

2.1空节点的最大贡献值为0；
2.2非空节点的最大贡献值等于节点值与其子节点中的最大贡献值之和（对于叶节点而言，最大贡献值等于节点值）。

解题方法

1.维护一个全局变量 maxSum 存储最大路径和，在递归过程中更新 maxSum 的值;
2.递归计算左右子节点的最大贡献值,只有在最大贡献值大于 0 时，才会选取对应子节点.(递归函数返回当前节点值加其左右子树的最大节点值之和)
3.在归的过程中，记录当前节点的最大路径和与maxSum比较，取二者中的较大值并更新maxSum

复杂度

时间复杂度:

$O(n)$

空间复杂度:

$O(n)$

Code

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {//记录最大的路径值int maxSum = Integer.MIN_VALUE;/*** Return the max path of a binary tree** @param root The root node of a binary tree* @return int*/public int maxPathSum(TreeNode root) {maxGain(root);return maxSum;}/*** Get the max path of a binary tree** @param node The node of a binary tree* @return int*/public int maxGain(TreeNode node) {if (node == null) {return 0;}/*(1).Recursively calculates the maximum contribution valueof the left and right child nodes(2).Only when the maximum contribution value is greater than 0,the corresponding child node is selected*/int leftGain = Math.max(maxGain(node.left), 0);int rightGain = Math.max(maxGain(node.right), 0);//The maximum path sum of a node depends on the value of this node// and the maximum contribution of nodes around this nodeint priceNewPath = node.val + leftGain + rightGain;//Update the max pathmaxSum = Math.max(maxSum, priceNewPath);return node.val + Math.max(leftGain, rightGain);}
}