数据结构学习笔记——二叉树的遍历和链式存储代码实现二叉树

目录

  • 一、二叉树的遍历
    • （一）二叉树的先序遍历（DLR）
    • （二）二叉树的中序遍历（LDR）
    • （三）二叉树的后序遍历（LRD）
    • （四）先序、中序和后序遍历的相关性质
    • （五）二叉树的层次遍历
  • 二、二叉树的实现代码（链式存储）
    • （一）二叉树的定义
    • （二）二叉树的建立
    • （三）广义表输出二叉树
    • （四）二叉树的先、中、后遍历
    • （五）二叉树的层次遍历
    • （六）二叉树的深度
    • （七）二叉树的叶子结点数
    • （八）二叉树的结点总数
  • ❤️循环队列的完整代码

一、二叉树的遍历

二叉树的遍历是按某种规定的顺序来对访问树中的所有结点，且每个结点仅被访问一次，由于二叉树由根结点（D）、左子树（L）和右子树（R）组成，可分为二叉树的先、中、后遍历另外还有每一层的遍历，即层次遍历，如下表：

遍历访问结点的顺序
先序遍历根左右
中序遍历左根右
后序遍历左右根

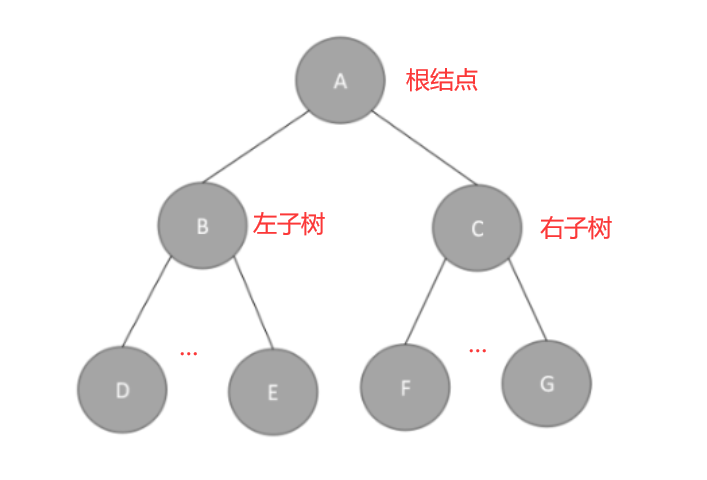
在这里插入图片描述

二叉树的先、中、后序遍历都可以通过递归算法实现，递归结束的条件是T==NULL，即当二叉树为空时，遍历结束。

（一）二叉树的先序遍历（DLR）

二叉树的先序遍历中，首先是根结点，遍历完根结点的左子树，然后再遍历完根结点的右子树，依次下去至所有结点都遍历到，例如下图二叉树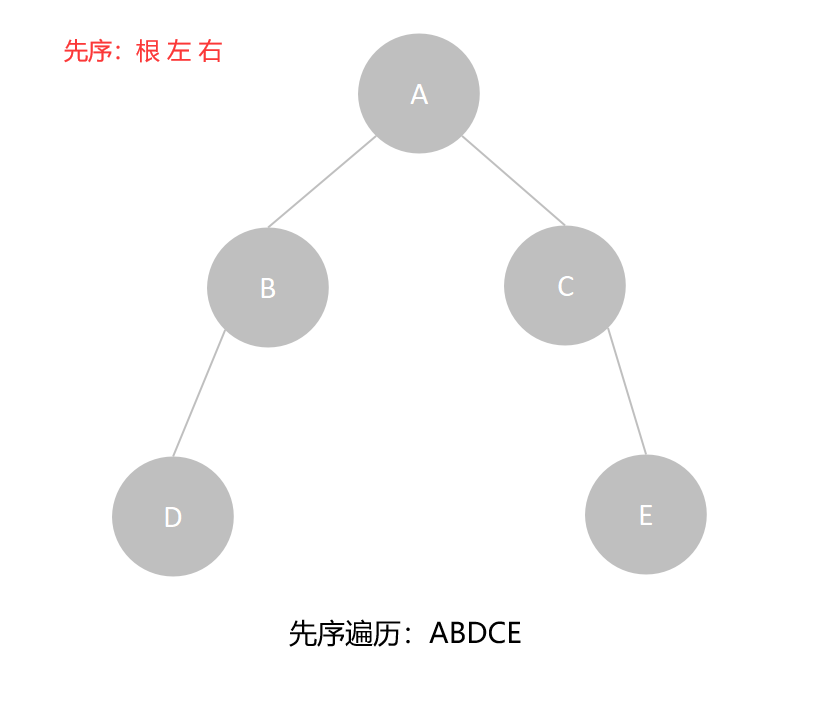：在这里插入图片描述

其先序遍历序列为ABDCE。

（二）二叉树的中序遍历（LDR）

二叉树的中序遍历中，首先是遍历完根结点的左子树，然后是根结点，最后遍历完根结点的右子树，依次下去至所有结点都遍历到，通过中序遍历可以得到一个递增的有序序列。

例如，一个二叉树中，根据中序遍历可知，中序遍历序列的最后一个结点一定是从根结点开始沿着右子树走到最底的结点，若它为叶子结点，则先序遍历序列和中序遍历序列的最后一个结点都为该结点；若不为叶子结点，它还有一个左子结点，则该左子结点是前序遍历序列的最后一个结点。

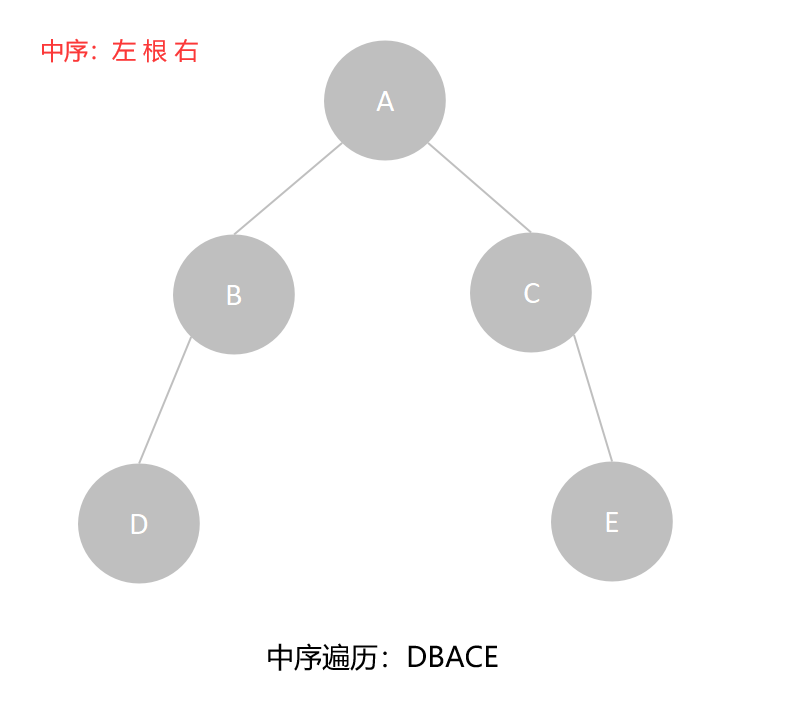
在这里插入图片描述
中序遍历序列为：DBACE，由于中序遍历序列的最后一个结点一定是从根结点开始沿着右子树走到最底的结点，所以中序遍历序列的最后一个结点为E，由于该结点是叶子结点，所以先序遍历序列和中序遍历序列的最后一个结点都为该结点。

先序：ABDCE
中序：DBACE

（三）二叉树的后序遍历（LRD）

二叉树的后序遍历中，首先是遍历完根结点的左子树，然后遍历完根结点的右子树，最后是根结点，依次下去至所有结点都遍历到，也就是从二叉树的底层往上层依次遍历。
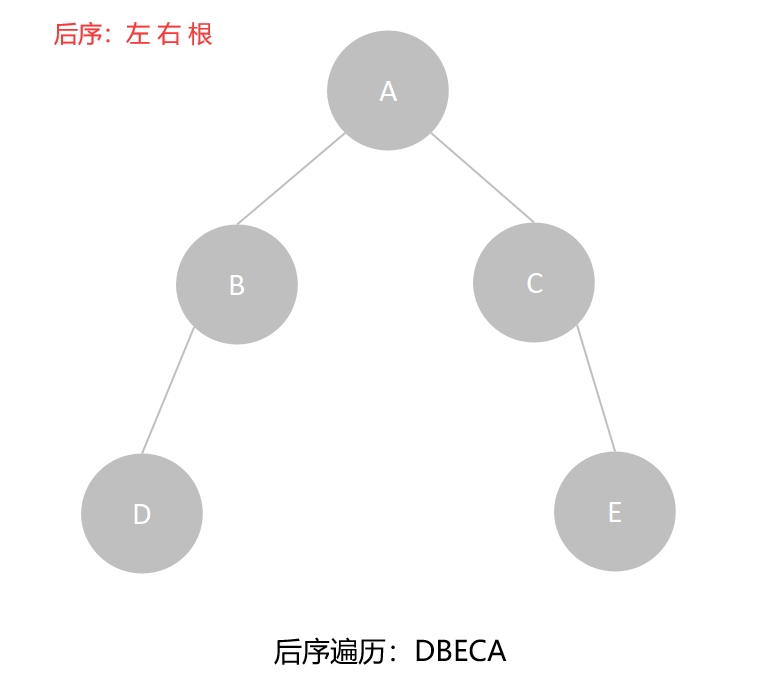
在这里插入图片描述
该二叉树的后序遍历序列为：DBECA。

（四）先序、中序和后序遍历的相关性质

  • 在二叉树的前序遍历、中序遍历和后序遍历序列中，所有叶子结点的先后顺序是相同的。

例如，该二叉树的三种遍历分别为ABDCE、DBACE、DBECA，可以看出叶子结点D和E的先后顺序总是一样的，D结点永远都在E结点的前面。
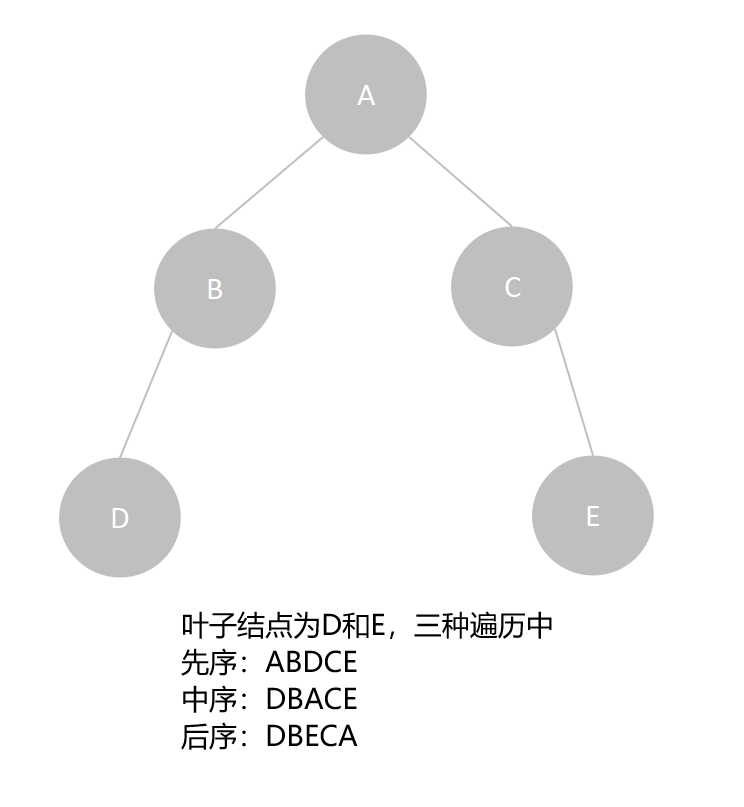
在这里插入图片描述

  • 若一棵二叉树为空树或只有根结点，则其先序遍历序列和后序遍历序列相同；若二叉树为单右支二叉树或孤立结点，则其先序遍历序列和中序遍历序列相同。

例如，下面单右支二叉树，先序遍历序列和中序遍历序列相同的，都为ABC：
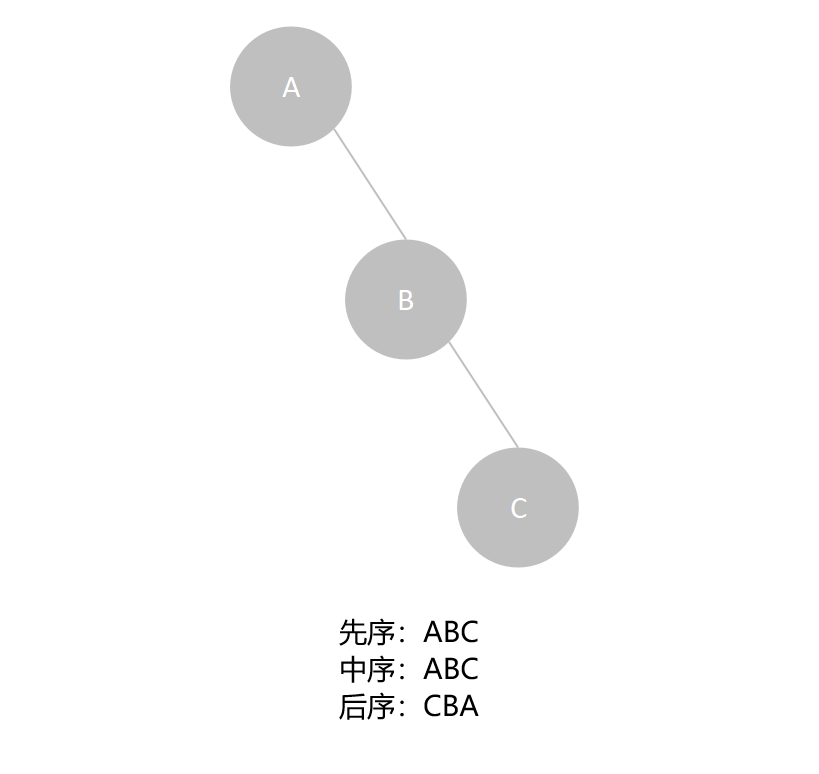
在这里插入图片描述

  • 若一棵二叉树为空树或任一结点都缺右子树的单支树，则其中序遍历序列和后序遍历序列相同。

例如，下面二叉树，其中任一结点至多只有左子树，中序遍历序列和后序遍历序列相同，都为DCBA：
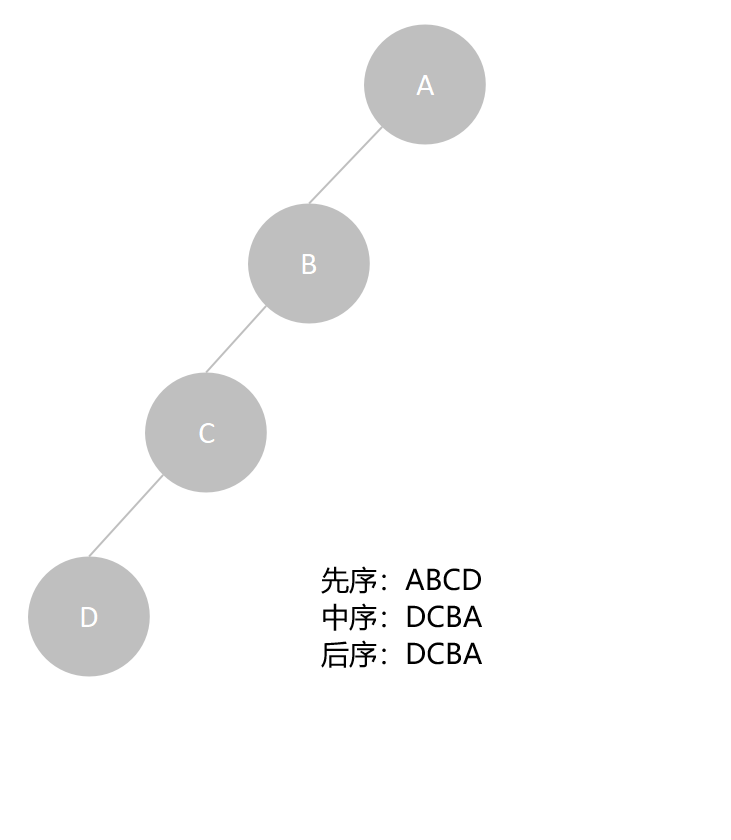
在这里插入图片描述

  • 若一棵非空的二叉树只有一个叶子结点，或二叉树的高度等于结点个数，则其先序遍历序列和后序遍历序列相反。

例如，下面二叉树只有一个叶子结点，其结点个数为3也等于高度h=3，所以其先序遍历序列和后序遍历序列相反，即ABC和CBA：
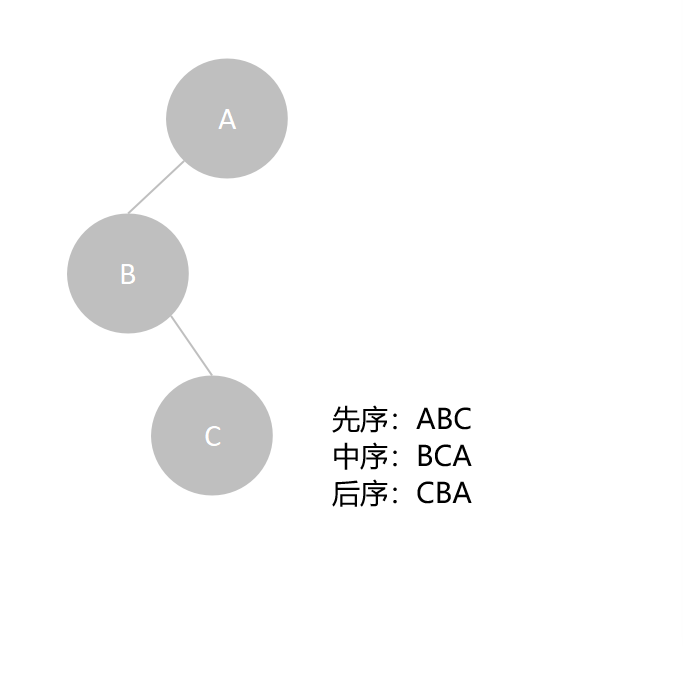
在这里插入图片描述

（五）二叉树的层次遍历

层次遍历中，层次优先，当对一层的结点都遍历完后，遍历下一层，按照次序对每个结点的左、右孩子进行遍历。
例如，下面二叉树，其层次遍历为ABCDEFG：
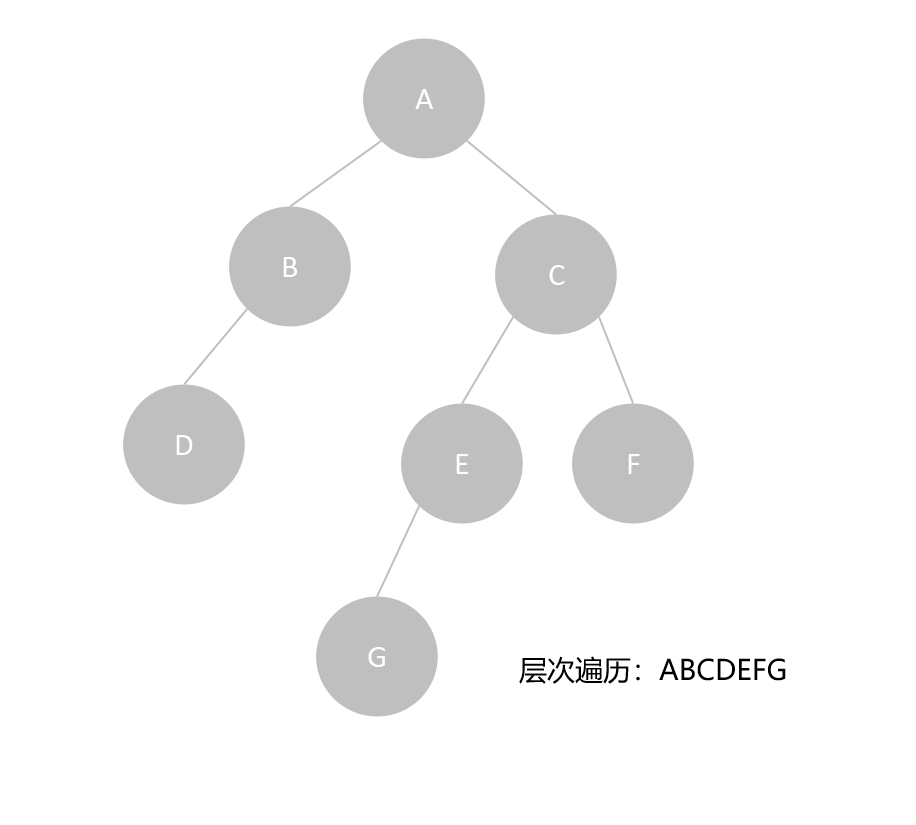
在这里插入图片描述
层次遍历二叉树中可以通过链式队列实现，首先二叉树的根结点入队，然后进入循环，循环条件为队列是否为空，若不为空，则当前队头结点出队，此时该结点被访问到，并将该结点的左、右孩子结点插入到队列的队尾。

  • 若一棵二叉树为空树或任一结点至多只有右子树，则中序遍历序列与层次遍历序列相同。

二、二叉树的实现代码（链式存储）

（一）二叉树的定义

通过链式存储结构实现代码如下，其中包含数据域和两个指针：

#incldue<stdio.h>
/*二叉树的定义*/
typedef struct BNode {int data;		//数据域struct BNode *lchild,*rchild;		//左孩子、右孩子指针
} *BTree;

（二）二叉树的建立

创建一个二叉树，按二叉树的顺序（二叉树带空指针的顺序，空指针也算进去），即根结点、左子树、右子树的顺序依次输入结点的值【使用的顺序是先序序列】，若其中有空结点，用0表示，其中使用到递归的方法建立左右孩子结点，实现代码如下：

#include <malloc.h>
/*二叉树的建立*/
BTree CreateTree() {BTree T;char ch;scanf("%c",&ch);getchar();	//getchar()用于接收每次输入字符结点后的回车符，从而以便输入下一个字符结点if(ch=='0')	//当为0时，将结点置空T=NULL;else {T=(BTree)malloc(sizeof(BTree));	//分配一个新的结点T->data=ch;printf("请输入%c结点的左孩子结点：",T->data);T->lchild=CreateTree();		//通过递归建立左孩子结点printf("请输入%c结点的右孩子结点：",T->data);T->rchild=CreateTree();		//通过递归建立右孩子结点}return T;
}

（三）广义表输出二叉树

通过广义表来显示建立的二叉树，一个非空的二叉树T，当对于左孩子结点或右孩子结点时，此时输出一个左括号“(”，递归处理左子树，输出一个“,”用于隔开结点，然后递归处理右子树，输出一个右括号“)”，从而完成一个根结点以下的两个左/右结点处理。

/*广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data);	//输入出该结点的数据域if(T->lchild!=NULL) {		//若该结点的左子树不为空printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {	//若该结点右子树不为空printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号} else {	//若左子树为空，右子树不为空if(T->rchild!=NULL) {printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {		//若该结点的右子树不为空	printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号}}}
}

例如，一个二叉树如下图，通过链式存储结构实现建立二叉树并输出。
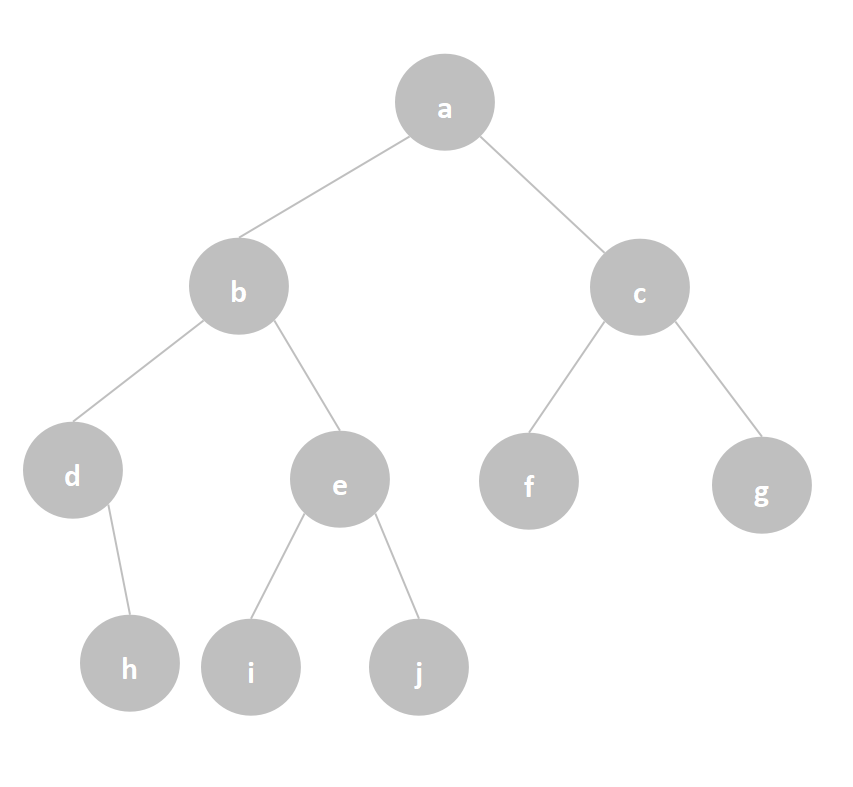
在这里插入图片描述
代码如下：

#include <stdio.h>
#include <malloc.h>
/*1、二叉树的定义*/
typedef struct BNode {int data;		//数据域struct BNode *lchild,*rchild;		//左孩子、右孩子指针
} *BTree;/*2、二叉树的建立*/
BTree CreateTree() {BTree T;char ch;scanf("%c",&ch);getchar();	//getchar()用于接收每次输入字符结点后的回车符，从而以便输入下一个字符结点if(ch=='0')	//当为0时，将结点置空T=NULL;else {T=(BTree)malloc(sizeof(BTree));	//分配一个新的结点T->data=ch;printf("请输入%c结点的左孩子结点：",T->data);T->lchild=CreateTree();		//通过递归建立左孩子结点printf("请输入%c结点的右孩子结点：",T->data);T->rchild=CreateTree();		//通过递归建立右孩子结点}return T;
}/*3、广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data);	//输入出该结点的数据域if(T->lchild!=NULL) {		//若该结点的左子树不为空printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {	//若该结点右子树不为空printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号} else {	//若左子树为空，右子树不为空if(T->rchild!=NULL) {printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {		//若该结点的右子树不为空	printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号}}}
}/*主函数*/
int main() {BTree T;T=NULL;printf("请输入二叉树的根结点：");T=CreateTree();		//建立二叉树printf("建立的二叉树如下：\n");ShowTree(T);		//通过广义表显示二叉树
}

依次输入各个结点的左右孩子结点，若结点不存在则输入0，例如树中结点d的左孩子结点不存在，结点f、g、h、i、j的左右孩子都不存在。
运行结果如下，结果通过广义表的定义显示：
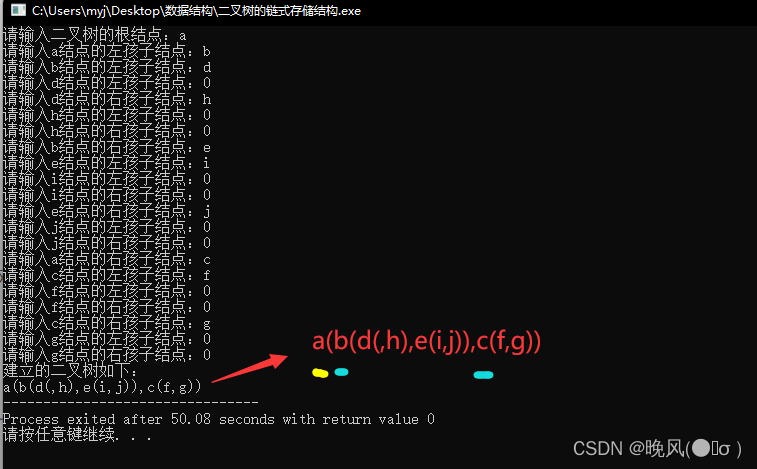
在这里插入图片描述

（四）二叉树的先、中、后遍历

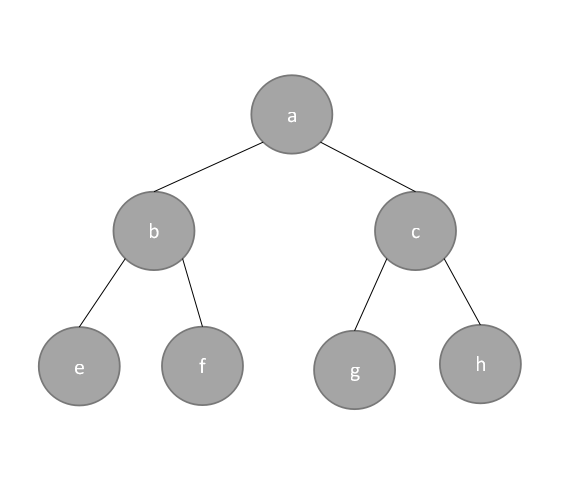
例如对下图这个二叉树，进行先、中、后遍历：
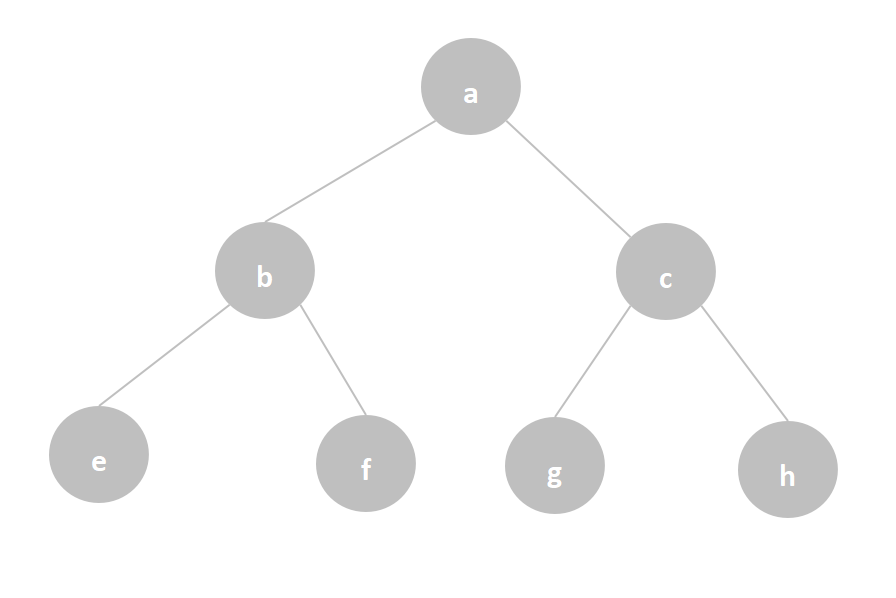
在这里插入图片描述
1、先序遍历二叉树：

/*先序遍历二叉树*/
bool ProTree(BTree T) {if(T==NULL)return false;			//递归结束else {printf("%c ",T->data);	//输出当前结点的数据域ProTree(T->lchild);		//递归继续遍历该结点的左子树ProTree(T->rchild);		//递归继续遍历该结点的右子树return true;}
}

运行结果如下：
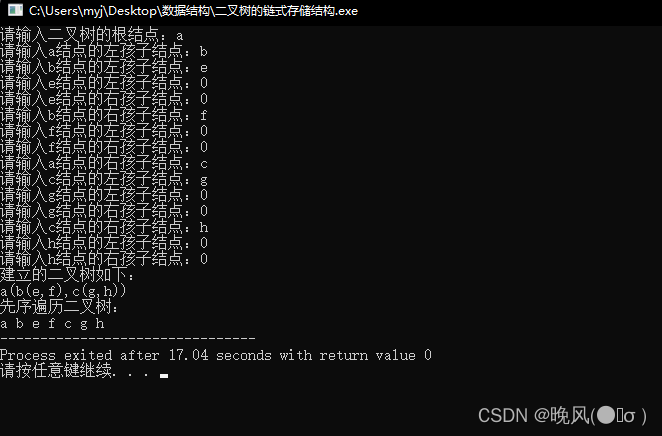
在这里插入图片描述
2、中序遍历二叉树：

/*中序遍历二叉树*/
bool InTree(BTree T) {if(T==NULL)return false;			//递归结束else {InTree(T->lchild);		//递归继续遍历该结点的左子树printf("%c ",T->data);	//输出当前结点的数据域InTree(T->rchild);		//递归继续遍历该结点的右子树return true;}
}

运行结果如下：
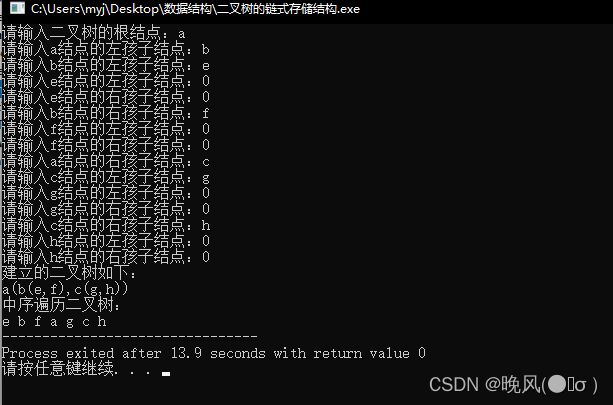
在这里插入图片描述
3、后序遍历二叉树：

/*后序遍历二叉树*/
bool PostTree(BTree T) {if(T==NULL)return false;				//递归结束else {PostTree(T->lchild);		//递归继续遍历该结点的左子树PostTree(T->rchild);		//递归继续遍历该结点的右子树printf("%c ",T->data);		//输出当前结点的数据域return true;}
}

运行结果如下：
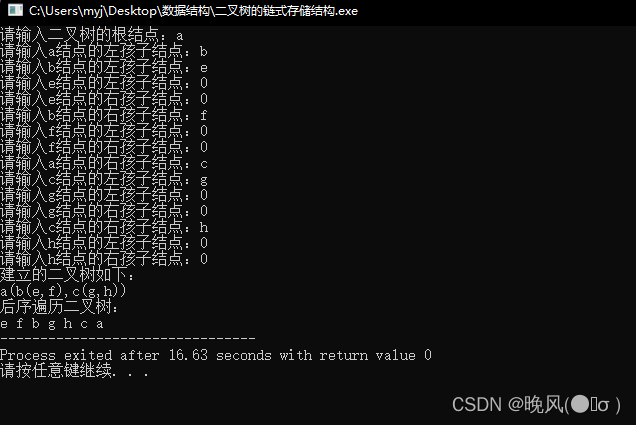
在这里插入图片描述

（五）二叉树的层次遍历

在这里插入图片描述
层次遍历二叉树：

/*7、层次遍历二叉树*/
void LevelTree(BTree T) {BTree q[MAXSIZE];		//MAXSIZE的值可自行定义int front=0,rear=0;		//初始化队头指针和队尾指针为0if(T!=NULL) {			//当二叉树不为空q[rear++]=T;					//根结点入队while(front!=rear) {			//当队列不为空时BTree head=q[front++];printf("%c ",head->data);	//访问队头结点的数据域if(head->lchild) 			//若当前结点的左孩子存在，将队头结点的左孩子入队q[rear++]=head->lchild;if(head->rchild) 			//若当前结点的右孩子存在，将队头结点的右孩子入队q[rear++]=head->rchild;}}
}

也是上图中的二叉树，进行层次遍历，运行结果如下：
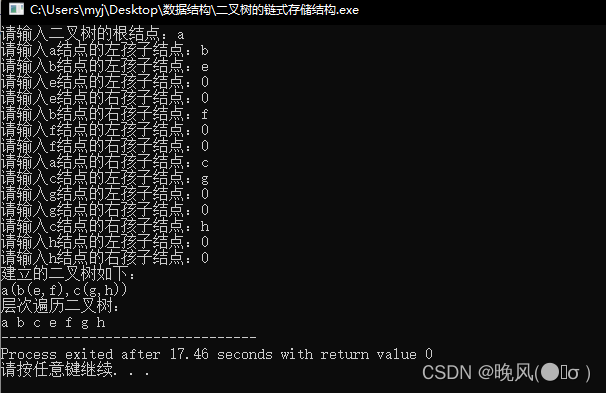
在这里插入图片描述

（六）二叉树的深度

二叉树的深度也是求最大深度，也是采用递归思想，分别递归计算左、右子树的深度，然后从左、右子树的深度中返回最大值，即为二叉树的深度，实现代码如下：

/*二叉树的深度*/
int DepthTree(BTree T) {int ldepth=0,rdepth=0;		//分别代表左、右子树的深度，初始值都为0if(T==NULL)return 0;else {ldepth=DepthTree(T->lchild);	//递归继续统计结点的左子树深度rdepth=DepthTree(T->rchild);	//递归继续统计结点的右子树深度if(ldepth>rdepth)		//求最大深度return ldepth+1;elsereturn rdepth+1;}
}

对于上图中的二叉树，运行结果如下：
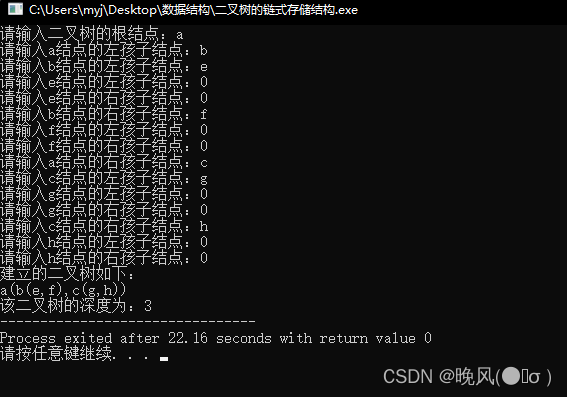
在这里插入图片描述

（七）二叉树的叶子结点数

求一个二叉树的叶子结点数，也是递归方法实现，我们知道若一个结点的左、右孩子都为空，则这说明这是一个叶子结点，通过递归，最后return返回叶子结点数，实现代码如下：

/*二叉树的叶子结点数*/
int LeavesNum(BTree T) {if(T!=NULL) {	//当根结点不为空if(T->lchild==NULL&&T->rchild==NULL)	//若一个结点的左、右孩子都为空，即这是一个叶子结点 return 1;}return (LeavesNum(T->lchild)+LeavesNum(T->rchild));
}

对于上图中的二叉树，运行结果如下：
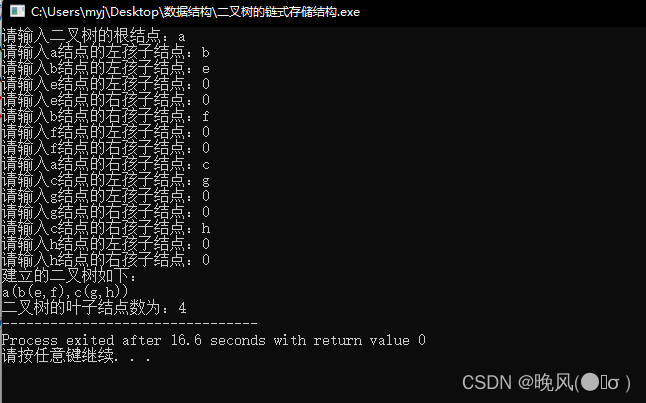
在这里插入图片描述

（八）二叉树的结点总数

也是递归，当二叉树不为空时，二叉树的结点总数等于左子树结点个数+右子树结点个数，然后加1（二叉树的根结点），实现代码如下：

/*求二叉树的结点总数*/
int SumLeaves(BTree T) {if(T!=NULL)return (SumLeaves(T->lchild)+SumLeaves(T->rchild)+1);
}

对于上图中的二叉树，运行结果如下：
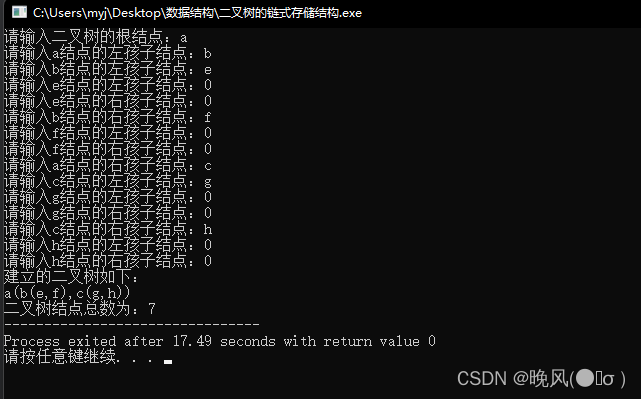
在这里插入图片描述

❤️循环队列的完整代码

循环队列的完整代码如下：

#incldue<stdio.h>
#include <malloc.h>
/*二叉树的定义*/
typedef struct BNode {int data;		//数据域struct BNode *lchild,*rchild;		//左孩子、右孩子指针
} *BTree;/*二叉树的建立*/
BTree CreateTree() {BTree T;char ch;scanf("%c",&ch);getchar();	//getchar()用于接收每次输入字符结点后的回车符，从而以便输入下一个字符结点if(ch=='0')	//当为0时，将结点置空T=NULL;else {T=(BTree)malloc(sizeof(BTree));	//分配一个新的结点T->data=ch;printf("请输入%c结点的左孩子结点：",T->data);T->lchild=CreateTree();		//通过递归建立左孩子结点printf("请输入%c结点的右孩子结点：",T->data);T->rchild=CreateTree();		//通过递归建立右孩子结点}return T;
}/*广义表输出二叉树*/
void ShowTree(BTree T) {if(T!=NULL) {//当二叉树不为空时printf("%c",T->data);	//输入出该结点的数据域if(T->lchild!=NULL) {		//若该结点的左子树不为空printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {	//若该结点右子树不为空printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号} else {	//若左子树为空，右子树不为空if(T->rchild!=NULL) {printf("(");	//输出一个左括号ShowTree(T->lchild);	//通过递归继续输出结点的左子树结点下的各结点if(T->rchild!=NULL) {		//若该结点的右子树不为空	printf(",");	//输出一个逗号ShowTree(T->rchild);	//通过递归继续输出结点的右子树结点下的各结点}printf(")");	//输出一个右括号}}}
}/*先序遍历二叉树*/
bool ProTree(BTree T) {if(T==NULL)return false;			//递归结束else {printf("%c ",T->data);	//输出当前结点的数据域ProTree(T->lchild);		//递归继续遍历该结点的左子树ProTree(T->rchild);		//递归继续遍历该结点的右子树return true;}
}/*中序遍历二叉树*/
bool InTree(BTree T) {if(T==NULL)return false;			//递归结束else {InTree(T->lchild);		//递归继续遍历该结点的左子树printf("%c ",T->data);	//输出当前结点的数据域InTree(T->rchild);		//递归继续遍历该结点的右子树return true;}
}/*后序遍历二叉树*/
bool PostTree(BTree T) {if(T==NULL)return false;				//递归结束else {PostTree(T->lchild);		//递归继续遍历该结点的左子树PostTree(T->rchild);		//递归继续遍历该结点的右子树printf("%c ",T->data);		//输出当前结点的数据域return true;}
}/*层次遍历二叉树*/
void LevelTree(BTree T) {BTree q[100];		//MAXSIZE的值可自行 定义int front=0,rear=0;		//初始化队头指针和队尾指针为0if(T!=NULL) {			//当二叉树不为空q[rear++]=T;					//根结点入队while(front!=rear) {			//当队列不为空时BTree head=q[front++];printf("%c ",head->data);	//访问队头结点的数据域if(head->lchild) 			//若当前结点的左孩子存在，将队头结点的左孩子入队q[rear++]=head->lchild;if(head->rchild) 			//若当前结点的右孩子存在，将队头结点的右孩子入队q[rear++]=head->rchild;}}
}/*二叉树的深度*/
int DepthTree(BTree T) {int ldepth=0,rdepth=0;		//分别代表左、右子树的深度，初始值都为0if(T==NULL)return 0;else {ldepth=DepthTree(T->lchild);	//递归继续统计结点的左子树深度rdepth=DepthTree(T->rchild);	//递归继续统计结点的右子树深度if(ldepth>rdepth)		//求最大深度return ldepth+1;elsereturn rdepth+1;}
}/*二叉树的叶子结点数*/
int LeavesNum(BTree T) {if(T!=NULL) {	//当根结点不为空if(T->lchild==NULL&&T->rchild==NULL)	//若一个结点的左、右孩子都为空，即这是一个叶子结点 return 1;}return (LeavesNum(T->lchild)+LeavesNum(T->rchild));
}/*求二叉树的结点总数*/
int SumLeaves(BTree T) {if(T!=NULL)return (SumLeaves(T->lchild)+SumLeaves(T->rchild)+1);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/195815.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

如何使用群晖管家结合内网穿透实现公网远程访问本地黑群晖

如何使用群晖管家结合内网穿透实现公网远程访问本地黑群晖

白嫖怪狂喜&#xff01;黑群晖也能使用群晖管家啦&#xff01; 文章目录 白嫖怪狂喜&#xff01;黑群晖也能使用群晖管家啦&#xff01;1.使用环境要求&#xff1a;2.下载安装群晖管家app3.随机地址登陆群晖管家app4.固定地址登陆群晖管家app 自己组装nas的白嫖怪们虽然也可以通…
阅读更多...
微信小程序引入node_modules依赖

微信小程序引入node_modules依赖

微信小程序不支持直接读取node_modules 首先在目录文件夹下cmd输入npm init命令 D:\小程序\project\calendar\calendar_1>npm init This utility will walk you through creating a package.json file. It only covers the most common items, and tries to guess sensible…
阅读更多...
linux resin的安装

linux resin的安装

1. 下载安装包 1.1 下载地址&#xff1a;https://caucho.com/products/resin/download 这里我下载的是普通版本的resin&#xff0c;没有选resin pro 版本。 科普一下&#xff0c;从性能上来说 resin和resin pro 版本的性能没区别。 resin pro 版本的 和resin 普通版本的文件是…
阅读更多...
无惧泄密：揭秘上海迅软DSE防拷贝大杀器！

无惧泄密：揭秘上海迅软DSE防拷贝大杀器！

对于企事业单位而言&#xff0c;文档的安全保护不仅要从源头上进行&#xff0c;杜绝文档在使用、传播过程中产生的泄密风险&#xff0c;同时也要对文档内容本身进行保护。为防止有心人通过拷贝、截屏、拍照等方式盗窃走重要文档内容信息的情况&#xff0c;天锐绿盾文件防泄密软…
阅读更多...
HTTP 缓存机制

HTTP 缓存机制

一、强制缓存 只要浏览器判断缓存没有过期&#xff0c;则直接使用浏览器的本地缓存而无需再请求服务器。 强制缓存是利用下面这两个 HTTP 响应头部&#xff08;Response Header&#xff09;字段实现的&#xff0c;它们都用来表示资源在客户端缓存的有效期&#xff1a; Cache…
阅读更多...
Python基础快速过一遍

Python基础快速过一遍

文章目录 一、变量及基本概念1、变量2、变量类型3、变量格式化输出4、type()函数5、input()函数6、类型转换函数7、注释 二、Python运算/字符1、算数运算2、比较运算3、逻辑运算4、赋值运算符5、转义字符6、成员运算符 三、判断/循环语句1、if判断语句2、while循环语句3、for循…
阅读更多...
等保测评报价相差很大，里面有什么门道

等保测评报价相差很大，里面有什么门道

等保测评报价的差异主要源于以下几点&#xff1a; 服务质量评估标准不同&#xff1a;不同的测评机构在测评过程中所提供的服务范围、深度、细节等方面可能存在差异&#xff0c;因此导致报价有所不同。一些机构可能提供全面且细致的测评服务&#xff0c;致力于提供高质量的等保测…
阅读更多...
openGauss学习笔记-139 openGauss 数据库运维-例行维护-检查应用连接数

openGauss学习笔记-139 openGauss 数据库运维-例行维护-检查应用连接数

文章目录 openGauss学习笔记-139 openGauss 数据库运维-例行维护-检查应用连接数139.1 操作步骤139.2 异常处理 openGauss学习笔记-139 openGauss 数据库运维-例行维护-检查应用连接数 如果应用程序与数据库的连接数超过最大值&#xff0c;则新的连接无法建立。建议每天检查连…
阅读更多...
一种结构新颖的双通带超导滤波器设计

一种结构新颖的双通带超导滤波器设计

闫鑫1,2&#xff0c;季来运1&#xff0c;张浩1,2&#xff0c;李颢毅1,2&#xff0c;王昭月1,2&#xff0c;曹凤莹1,2 &#xff08;1.天津海芯电子有限公司&#xff0c;天津300380&#xff1b;2.天津师范大学物理与材料科学学院&#xff0c;天津 300387.&#xff09; 摘要&…
阅读更多...
前端dark主题的快速构建与切换

前端dark主题的快速构建与切换

首先在全局css样式中增加一个 dark 模式即可&#xff0c;主要就是filter这个属性&#xff0c; invert(1);则表示100%完全反转样式&#xff0c;通俗点就是颠倒黑白&#xff0c;白的让它变成黑的&#xff0c;黑的让它变成白的。 css中的filter函数总结 filter:invert(1);数值范围…
阅读更多...
Leetcode题库（数据库合集）_ 难度：简单

Leetcode题库（数据库合集）_ 难度：简单

目录 难度&#xff1a;简单1. 组合两个表2. 第二高的薪水3. 第N高的薪水4. 分数排名5. 连续出现的数字6. 超过经理收入的员工7. 重新8. 寻找用户推荐人9. 销售员10. 排名靠前的旅行者11. 患某种疾病的患者12. 修复表中的名字13. 求关注者的数量14. 可回收且低脂的产品15. 计算特…
阅读更多...
前后端参数传递总结

前后端参数传递总结

1、 页面参数 js传递参数 渲染表格 页面控制器&#xff08;前端&#xff09; 后端控制器 后端服务 实体赋值 2、跟踪情况
阅读更多...
场景实践 | 法大大落地业财一体化，优化流程结构

场景实践 | 法大大落地业财一体化，优化流程结构

2023 年&#xff0c;法大大作为中国电子签行业唯一上榜《2023胡润全球未来独角兽》企业&#xff0c;同时上榜“2022深圳市潜在科技独角兽企业榜单”。作为高速发展的高科技服务企业&#xff0c;法大大自2021年完成9亿元腾讯D轮融资后&#xff0c;建立了长期主义发展计划&#x…
阅读更多...
计算机基础知识63

计算机基础知识63

Django的条件查询&#xff1a;查询函数 exclude exclude&#xff1a;返回不满足条件的数据 res Author.objects.exclude(pk1) print(res) # <QuerySet [<Author: Author object (2)>, <Author: Author object (3)>]> order_by 1、按照 id 升序排序 res …
阅读更多...
【Seata源码学习 】篇六 全局事务提交与回滚

【Seata源码学习 】篇六 全局事务提交与回滚

【Seata源码学习 】篇六 全局事务提交与回滚 全局事务提交 TM在RPC远程调用RM后,如果没有出现异常&#xff0c;将向TC发送提交全局事务请求io.seata.tm.api.TransactionalTemplate#execute public Object execute(TransactionalExecutor business) throws Throwable {// 1. …
阅读更多...
【离散数学】——期末刷题题库（集合）

【离散数学】——期末刷题题库（集合）

&#x1f383;个人专栏&#xff1a; &#x1f42c; 算法设计与分析&#xff1a;算法设计与分析_IT闫的博客-CSDN博客 &#x1f433;Java基础&#xff1a;Java基础_IT闫的博客-CSDN博客 &#x1f40b;c语言&#xff1a;c语言_IT闫的博客-CSDN博客 &#x1f41f;MySQL&#xff1a…
阅读更多...
【FPGA】Verilog：二进制并行加法器 | 超前进位 | 实现 4 位二进制并行加法器和减法器 | MSI/LSI 运算电路

【FPGA】Verilog：二进制并行加法器 | 超前进位 | 实现 4 位二进制并行加法器和减法器 | MSI/LSI 运算电路

Ⅰ. 前置知识 0x00 并行加法器和减法器 如果我们要对 4 位加法器和减法器进行关于二进制并行运算功能&#xff0c;可以通过将加法器和减法器以 N 个并行连接的方式&#xff0c;创建一个执行 N 位加法和减法运算的电路。 4 位二进制并行加法器 4 位二进制并行减法器 换…
阅读更多...
内存是如何工作的

内存是如何工作的

一、什么是内存 从外观上辨识&#xff0c;它就是内存条&#xff1b;从硬件上讲&#xff0c;它叫RAM&#xff0c;翻译过来叫随机存储器。英文全称&#xff1a;Random Access Memory。它也叫主存&#xff0c;是与CPU直接交换数据的内部存储器。其特点是读写速度快&#xff0c;不…
阅读更多...
java开发之个微机器人的实现

java开发之个微机器人的实现

简要描述&#xff1a; 二次登录 请求URL&#xff1a; http://域名地址/secondLogin 请求方式&#xff1a; POST 请求头Headers&#xff1a; Content-Type&#xff1a;application/jsonAuthorization&#xff1a;login接口返回 参数&#xff1a; 参数名必选类型说明wcId…
阅读更多...
【每日一题】从二叉搜索树到更大和树

【每日一题】从二叉搜索树到更大和树

文章目录 Tag题目来源题目解读解题思路方法一&#xff1a;中序遍历的反序方法二&#xff1a;后缀数组 写在最后 Tag 【中序遍历】【二叉树】【2023-12-04】 题目来源 1038. 从二叉搜索树到更大和树 题目解读 在二叉搜索树中&#xff0c;将每一个节点的值替换成树中大于等于该…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023