文章目录
- 06 g2o 学习
- 6.1 概念
- 6.2 框架简介
- 6.3 代码示例
06 g2o 学习
6.1 概念
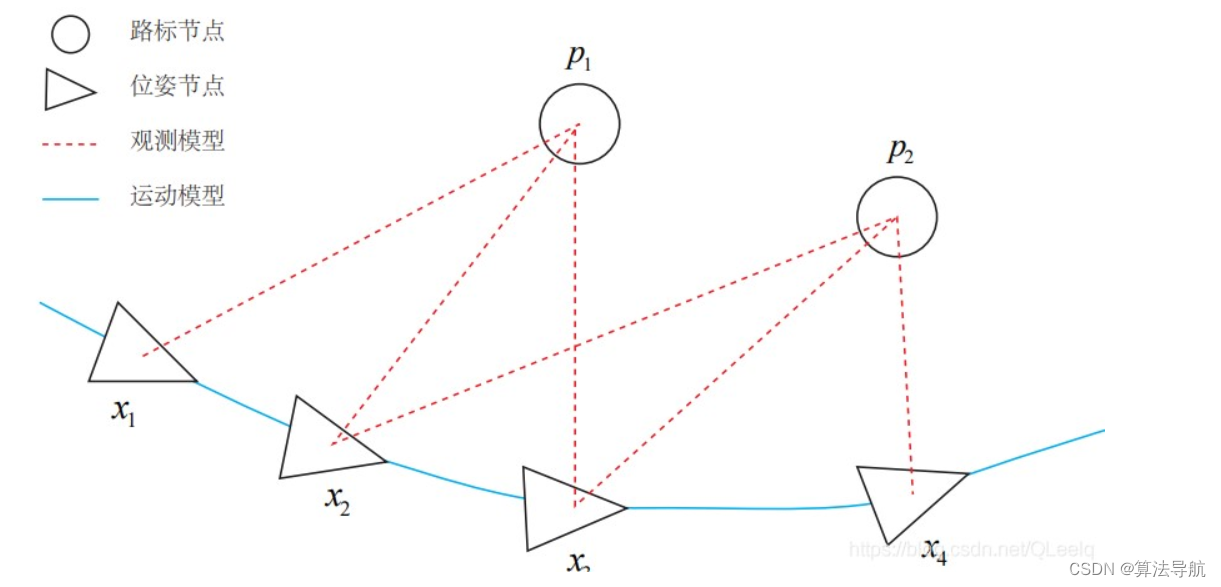
g2o(General Graphic Optimization)是基于图优化的库。图优化是把优化问题表现成图的一种方式。一个图由若干个顶点(Vertex),以及连接这这些顶点的边(Edge)组成。用顶点表示优化变量,用边表示误差项。
那么在 SLAM 中,不同时刻的位姿和路标点为待优化变量即顶点,将他们之间的观测作为边。数学表述为,传感器的观测方程
z k = h ( x k ) z_{k}=h\left(x_{k}\right) zk=h(xk)
实际上二者并不会相等,而是有误差存在
e k = z k − h ( x k ) e_k=z_k-h\left(x_k\right) ek=zk−h(xk)
于是,位姿 x k x_k xk 和 路标 z k z_k zk 为待优化变量(图中节点),误差 e k e_k ek 为约束(红色虚线)。
6.2 框架简介

几个需要注意的点:
(1)迭代形式为 H Δ x = b H\Delta x=b HΔx=b,也就是求出每次迭代步长 Δ x \Delta x Δx,三个算法可选:高斯牛顿、LM 和 Dog-Leg;
(2)定义顶点:顶点也就是待优化变量,它继承自基础类 BaseVertex<D, T>,其中 D 为 int 类型,表示维度,T 为数据类型。例如
g2o::BaseVertex<3, Eigen::Vector3d> // 三维点,Eigen::Vector3d 类型g2o::BaseVertex<6, SE3Quat> // SE3 变换矩阵,6个参数(平移+旋转)
(3)顶点更新:对于一般的函数,更新策略是 x k + 1 = x k + Δ x x_{k+1}=x_k+\Delta x xk+1=xk+Δx,也就是加上求出的 Δ x \Delta x Δx,而对于位姿 S E ( 3 ) SE(3) SE(3) 这样的数据类型类型来说,要用乘法。
// 顶点更新函数
void curveVetex::oplusImpl(const double* update)
{_estimate += Eigen::Vector3d(update); // 加法更新
}
(4)添加顶点,有多少个顶点就添加多少个。
// 新建顶点
curveVetex* v = new curveVetex(); // 自定义顶点类型
v->setEstimate(Eigen::Vector3d(0,0,0)); // 初始化
v->setId(0); // 设置 Id
optimizer.addVertex(v); // 加入优化器中
(5)定义边:包括一元边、二元边和多元边。误差=测量值-估计值
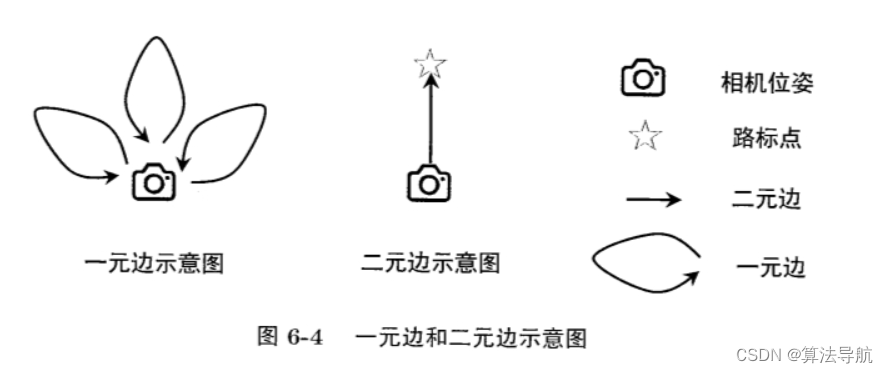
以二元边为例
g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type> // Vertex1Type 连接的顶点的类名
(6)添加边
EdgePointOnCurve* e = new EdgePointOnCurve;
e->setId(0); // 设置 Id
e->setInformation(Eigen::Matrix<double,1,1>::Identity()); // 信息矩阵
e->setVertex(0, v); // 设置连接的顶点
e->setMeasurement(y_data[i]); // 观测值
optimizer.addEdge(e);
(7)主要步骤
- 定义顶点和边的类型
- 构建图(添加顶点和边)
- 选择优化算法
- 调用 g2o 进行优化,返回结果
通用模板
// 1. 定义顶点
class curveVetex: public g2o::BaseVertex<3,Eigen::Vector3d>
{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWvirtual void setToOriginImpl(); // 顶点初始值,置零virtual void oplusImpl(const double* update); // 更新virtual bool read(std::istream &is); // 读盘、存盘,留空即可virtual bool write(std::ostream &os) const;
};// 2. 添加顶点
curveVetex* v = new curveVetex(); // 自定义顶点类型
v->setEstimate(Eigen::Vector3d(0,0,0)); // 初始化
v->setId(0); // 设置 Id
optimizer.addVertex(v); // 加入优化器中// 3. 定义边
class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWmyEdge(){}// 计算曲线模型误差=测量值-估计值void computeError();//存取bool read(std::istream& is);bool write(std::ostream& os) const;// 增量计算函数:误差对优化变量的偏导数void linearizeOplus();
}// 4. 添加边
EdgePointOnCurve* e = new EdgePointOnCurve;
e->setId(0); // 设置 Id
e->setInformation(Eigen::Matrix<double,1,1>::Identity()); // 信息矩阵
e->setVertex(0, v); // 设置连接的顶点
e->setMeasurement(y_data[i]); // 观测值
optimizer.addEdge(e);
6.3 代码示例
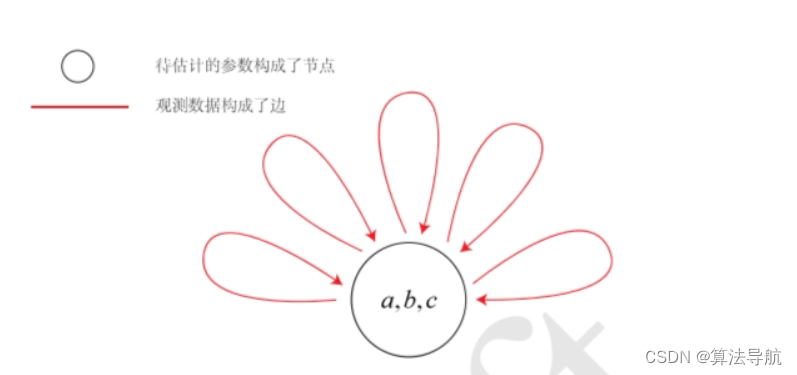
拟合函数 y = exp ( a x 2 + b x + c ) y=\exp(ax^2+bx+c) y=exp(ax2+bx+c)。
显然待优化变量为 a b c abc abc,只有一个顶点;误差值=观测值(实际值)-估计值(理论值),一元边。
需要注意的是,这里用的三种优化算法,都是误差 e i e_i ei 对代优化变量的偏导数,而不是 F ( x ) \boldsymbol{F}(x) F(x),即
e i = y i − e x p ( a x i 2 + b i x + c ) e_i=y_i-exp(ax_i^2+b_ix+c) ei=yi−exp(axi2+bix+c)
∂ e i ∂ a = − x i 2 exp ( a x i 2 + b i x + c ) ∂ e i ∂ b = − x i exp ( a x i 2 + b i x + c ) ∂ e i ∂ c = − exp ( a x i 2 + b i x + c ) \frac{ \partial e_i }{ \partial a}=-x_i^2\exp(ax_i^2+b_ix+c) \\ \frac{ \partial e_i }{ \partial b}=-x_i\exp(ax_i^2+b_ix+c) \\ \frac{ \partial e_i }{ \partial c}=-\exp(ax_i^2+b_ix+c) ∂a∂ei=−xi2exp(axi2+bix+c)∂b∂ei=−xiexp(axi2+bix+c)∂c∂ei=−exp(axi2+bix+c)
关于 g2o 使用的几个问题
(1)安装:
安装依赖项:
sudo apt-get install libqt4-dev qt4-qmake libqglviewer-dev libsuitesparse-dev libcxsparse3.1.2 libcholmod-dev
安装下列命令依次执行安装:
git clone https://github.com/RainerKuemmerle/g2o.git
cd g2o
mkdir build
cd build
cmake ..
make
sudo make install
安装完成后在目录/usr/local/includ 下能找到 g2o 目录,在 /usr/local/lib 下能找到libg2o_**.so的文件。
(2)cmakelists.txt
include_directories( ${G2O_INCLUDE_DIRS})
SET(G2O_LIBS g2o_cli g2o_ext_freeglut_minimal g2o_simulator g2o_solver_slam2d_linear g2o_types_icp g2o_types_slam2d g2o_core g2o_interface g2o_solver_csparse g2o_solver_structure_only g2o_types_sba g2o_types_slam3d g2o_csparse_extension g2o_opengl_helper g2o_solver_dense g2o_stuff g2o_types_sclam2d g2o_parser g2o_solver_pcg g2o_types_data g2o_types_sim3 cxsparse )include_directories("/usr/include/eigen3")add_executable(g2oCurveFitting ./src/g2oCurveFitting.cpp)
target_link_libraries(g2oCurveFitting ${G2O_LIBS})
(3)编译过程中遇到如下错误
error while loading shared libraries: libg2o_core.so: cannot open shared object file: No such file or directory出现这个问题的主要原因是,新安装的 g2o 没能生效。执行
sudo ldconfig
代码
/*********************************************************** *
* Time: 2023/8/27
* Author: xiaocong
* Function: g2o
* 注意这里用的是 ae * xi * xi + be * xi + sin(ce)
***********************************************************/#include <iostream>
#include <g2o/core/g2o_core_api.h>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_dogleg.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <eigen3/Eigen/Core>
#include <cmath>const int N = 100; // 数据点个数using namespace std;// 定义顶点即待优化变量 abc
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW// 设置初始值virtual void setToOriginImpl(){_estimate << 0, 0, 0;}// 更新,直接加上 delta_xvirtual void oplusImpl(const double* update){_estimate += Eigen::Vector3d(update);}// 存盘和读盘:留空virtual bool read(istream& in) {}virtual bool write(ostream& out) const {}
};// 定义边,包括误差项及其对优化变量的偏导数
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex>
{
public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;// 构造函数CurveFittingEdge(double x) : _x(x) {}// 计算曲线模型误差=测量值-估计值virtual void computeError(){// 取出 _vertices 中的第一个顶点,强制转换为 CurveFittingVertex* 类型const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);const Eigen::Vector3d abc = v->estimate();_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));}// 计算误差对优化变量的雅可比矩阵virtual void linearizeOplus(){const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);const Eigen::Vector3d abc = v->estimate();double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);_jacobianOplusXi[0] = -_x * _x * y;_jacobianOplusXi[1] = -_x * y;_jacobianOplusXi[2] = -y;}// 存盘和读盘:留空virtual bool read(istream& in) {}virtual bool write(ostream& out) const {}public:double _x; //x 值, y 值为 _measurement
};int main()
{double ar = 1.0, br = 2.0, cr = 1.0; // 真实参数值// 生成数据vector<double> x_data, y_data;for (int i = 0; i < N; i++){double xi = i / 100.0; // [0~1]double sigma = 0.02 * (rand() % 1000) / 1000.0 - 0.01; // 随机噪声,[-0.01, 0.01]double yi = exp(ar * xi * xi + br * xi + cr) + sigma;x_data.push_back(xi);y_data.push_back(yi);}// 构建图优化typedef g2o::BlockSolver< g2o::BlockSolverTraits<3, 1> > Block; // 每个误差项优化变量维度为3,误差值维度为1Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器Block* solver_ptr = new Block(linearSolver); // 矩阵块求解器// 高斯牛顿法优化 g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton(solver_ptr);g2o::SparseOptimizer optimizer; // 图模型optimizer.setAlgorithm(solver); // 设置求解器optimizer.setVerbose(true); // 打开调试输出// 向图中添加顶点(只有一个顶点)CurveFittingVertex* v = new CurveFittingVertex();v->setEstimate(Eigen::Vector3d(0, 0, 0)); // 初始值v->setId(0); // 顶点序号optimizer.addVertex(v); // 加入优化器// 向图中添加边for (int i = 0; i < N; i++){CurveFittingEdge* e = new CurveFittingEdge(x_data[i]);e->setId(i); // 设置 Ide->setVertex(0, v); // 连接的顶点e->setMeasurement(y_data[i]); // 观测值e->setInformation(Eigen::Matrix<double, 1, 1>::Identity()); // 信息矩阵optimizer.addEdge(e); // 加入优化器}// 执行优化cout << "start optimization" << endl;optimizer.initializeOptimization();optimizer.optimize(100); // 最大迭代次数// 输出优化值Eigen::Vector3d abc_estimate = v->estimate();cout << "result: " << abc_estimate.transpose() << endl;return 0;
}
结果
result: 0.999313 2.00098 0.999658


,一起修炼算法经法!)


的返回值)

。Javaee项目,springboot项目。)




)


覆盖优化 - 附代码)


)
